|
|
Краткая теория для выполнения лабораторных работ по курсу оту
По принципу управления САУ можно разбить на три группы:
С регулированием по внешнему воздействию - принцип Понселе (применяется в незамкнутых САУ).
С регулированием по отклонению - принцип Ползунова-Уатта (применяется в замкнутых САУ).
С комбинированным регулированием. В этом случае САУ содержит замкнутый и разомкнутый контуры регулирования.
Принцип управления по внешнему возмущению
В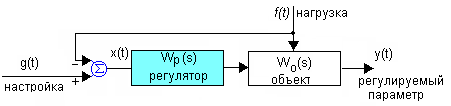 структуре обязательны датчики возмущения. Система описывается передаточной функцией разомкнутой системы: x(t) = g(t) - f(t). структуре обязательны датчики возмущения. Система описывается передаточной функцией разомкнутой системы: x(t) = g(t) - f(t).
Достоинства:
Можно добиться полной инвариантности к определенным возмущениям.
Не возникает проблема устойчивости системы, т.к. нет ОС.
Недостатки:
Большое количество возмущений требует соответствующего количества компенсационных каналов.
Изменения параметров регулируемого объекта приводят к появлению ошибок в управлении.
Можно применять только к тем объектам, чьи характеристики четко известны.
Принцип управления по отклонению
С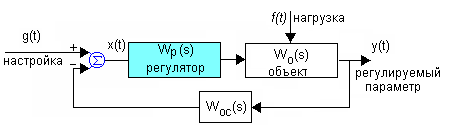 истема описывается передаточной функцией разомкнутой системы и уравнением замыкания: x(t) = g(t) - y(t) Woc(t). Алгоритм работы системы заключен в стремлении свести ошибку x(t) к нулю. истема описывается передаточной функцией разомкнутой системы и уравнением замыкания: x(t) = g(t) - y(t) Woc(t). Алгоритм работы системы заключен в стремлении свести ошибку x(t) к нулю.
Достоинства:
ООС приводит к уменьшению ошибки не зависимо от факторов ее вызвавших (изменений параметров регулируемого объекта или внешних условий).
Недостатки:
В системах с ОС возникает проблема устойчивости.
В системах принципиально невозможно добиться абсолютной инвариантности к возмущениям. Стремление добиться частичной инвариантности (не 1-ыми ОС) приводит к усложнению системы и ухудшению устойчивости.
К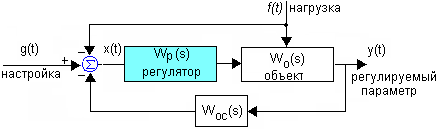 омбинированное управление омбинированное управление
Комбинированное управление заключено в сочетании двух принципов управления по отклонению и внешнему возмущению. Т.е. сигнал управления на объект формируется двумя каналами. Первый канал чувствителен к отклонению регулируемой величины от задания. Второй формирует управляющее воздействие непосредственно из задающего или возмущающего сигнала.
x(t) = g(t) - f(t) - y(t)Woc(t)
Достоинства:
Недостатки:
Каналы, чувствительные к заданию или к возмущению, обычно содержат дифференцирующие звенья. Их практическая реализация затруднена.
Не все объекты допускают форсирование.
6. Анализ устойчивости САР
Понятие устойчивости системы регулирования связано с ее способностью возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния. Устойчивость является одним из главных требований, предъявляемых к автоматическим системам.
Понятие устойчивости можно распространить и на случай движения САР:
невозмущенное движение,
возмущенное движение.
Движение любой СУ описывается с помощью дифференциального уравнения, которое в общем случае описывает 2 режима работы системы:
При этом общее решение в любой системе можно записать в виде:
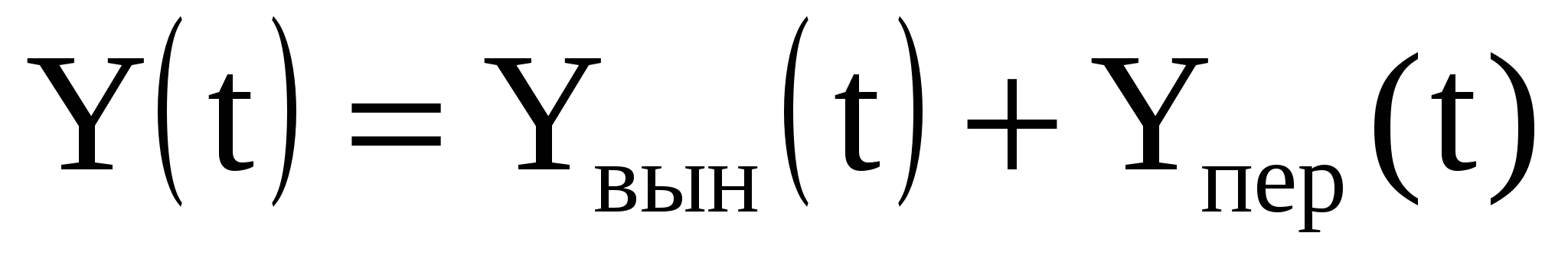
Вынужденная составляющая определяется входным воздействием на вход СУ. Этого состояния система достигает по окончании переходных процессов.
П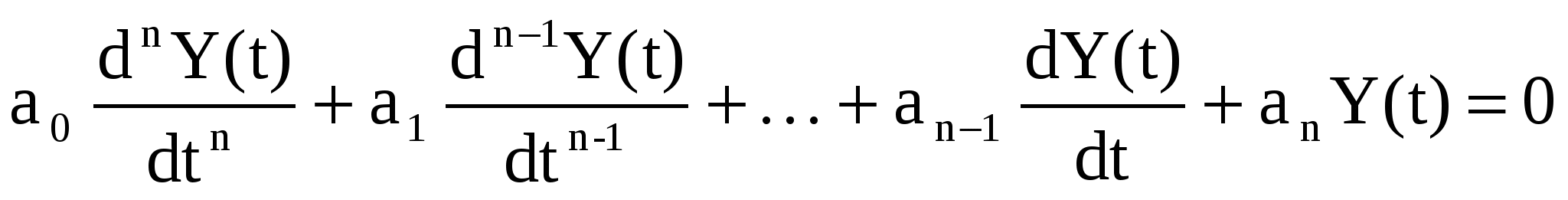 ереходная составляющая определяется решением однородного дифференциального уравнения вида: ереходная составляющая определяется решением однородного дифференциального уравнения вида:
Коэффициенты a0,a1,…an включают в себя параметры системы => изменение любого коэффициента дифференциального уравнения приводит к изменению целого ряда параметров системы.
Решение однородного дифференциального уравнения
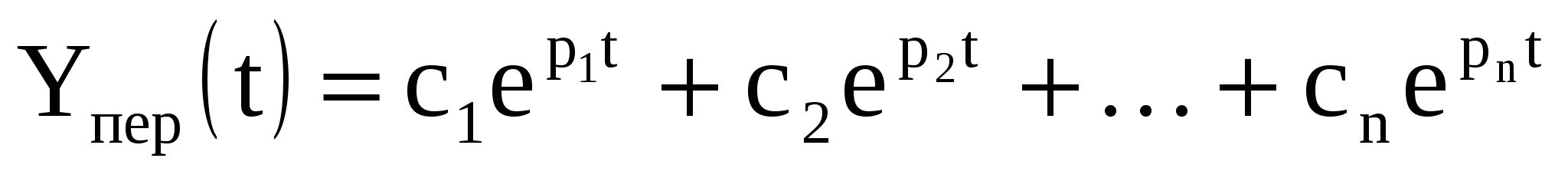
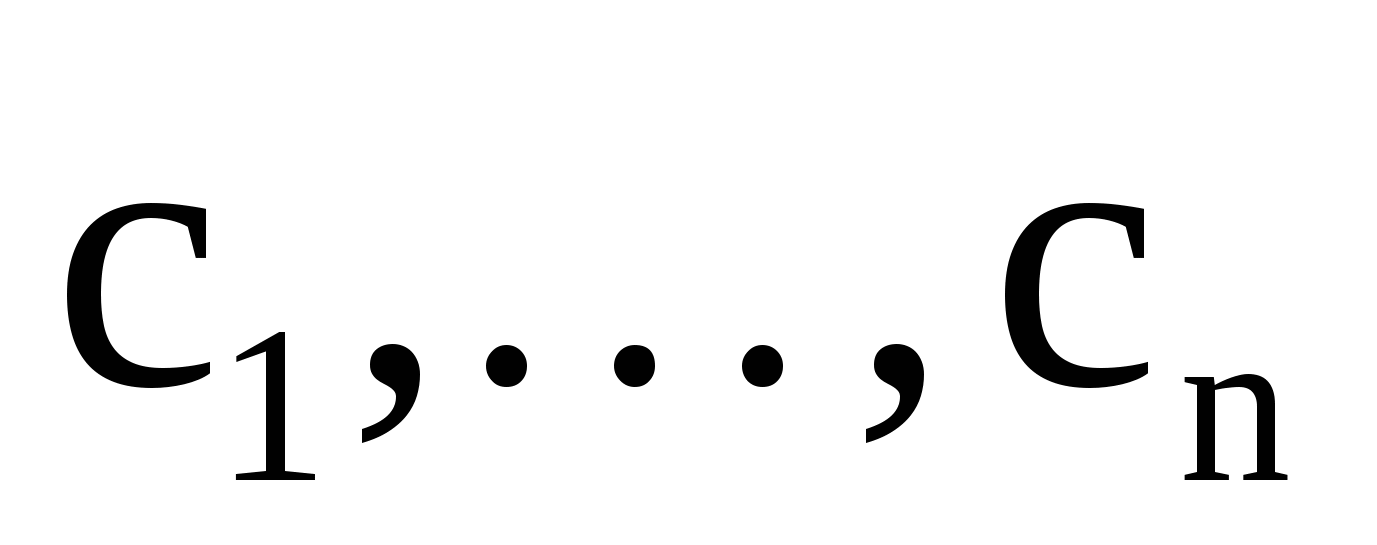 
где постоянные интегрирования, а – корни характеристического уравнения следующего вида:
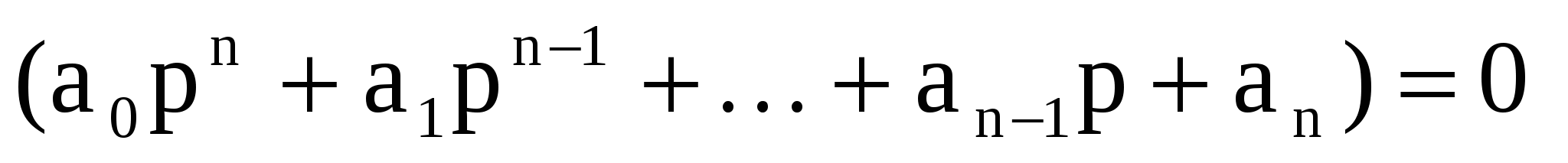
Характеристическое уравнение представляет собой знаменатель передаточной функции приравненный к нулю.
Корни характеристического уравнения могут быть вещественными, комплексно-сопряженными и комплексными, что определяется параметрами системы.
Чтобы оценивать устойчивость систем, разработан ряд критериев устойчивости
Все критерии устойчивости делятся на 3 группы:
корневые
а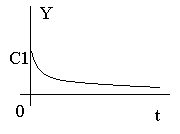 лгебраические лгебраические
частотные
6.1. Корневые критерии устойчивости
1) 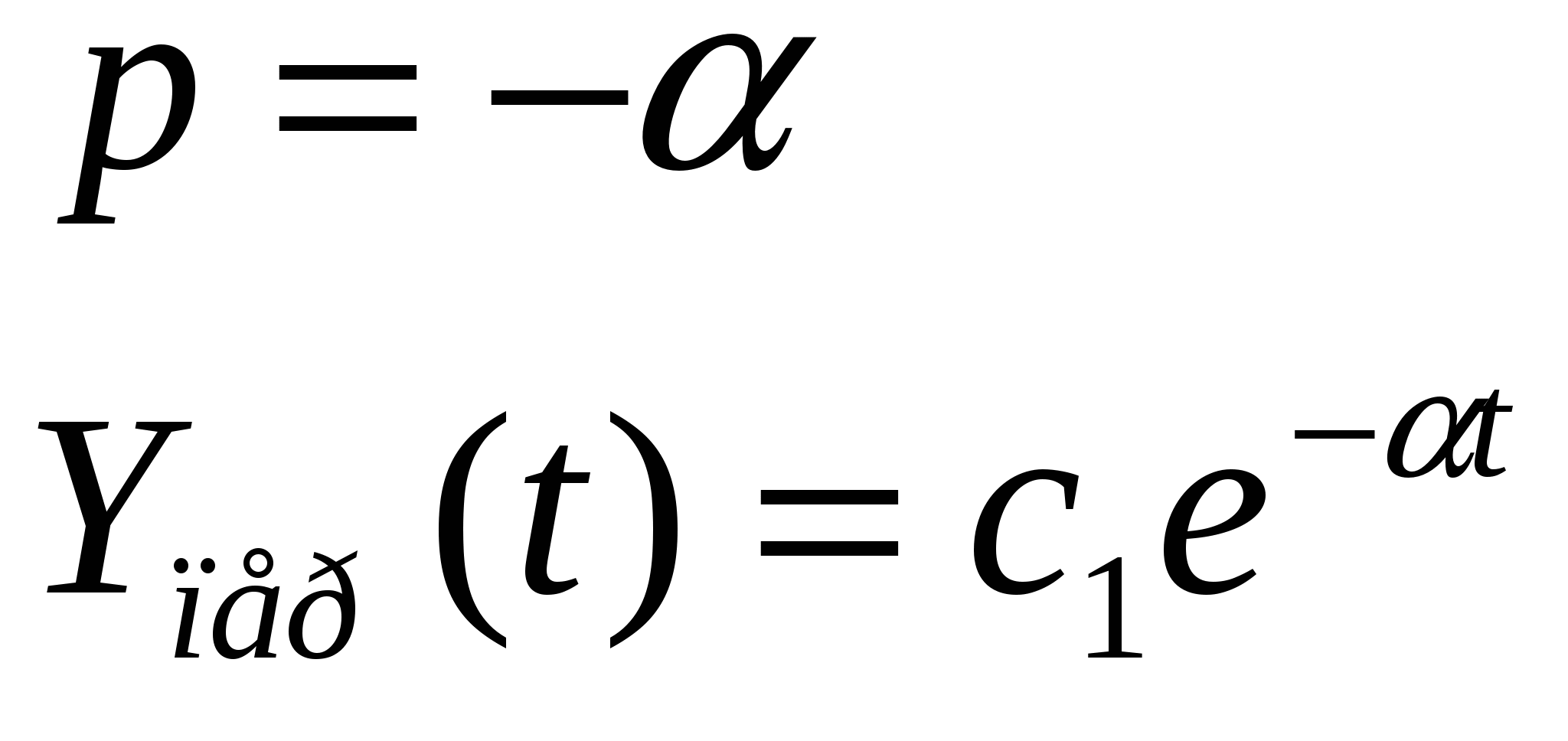 отрицательная вещественная часть отрицательная вещественная часть
затухающий процесс
Устойчивая система.
2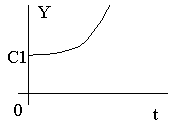 ) ) 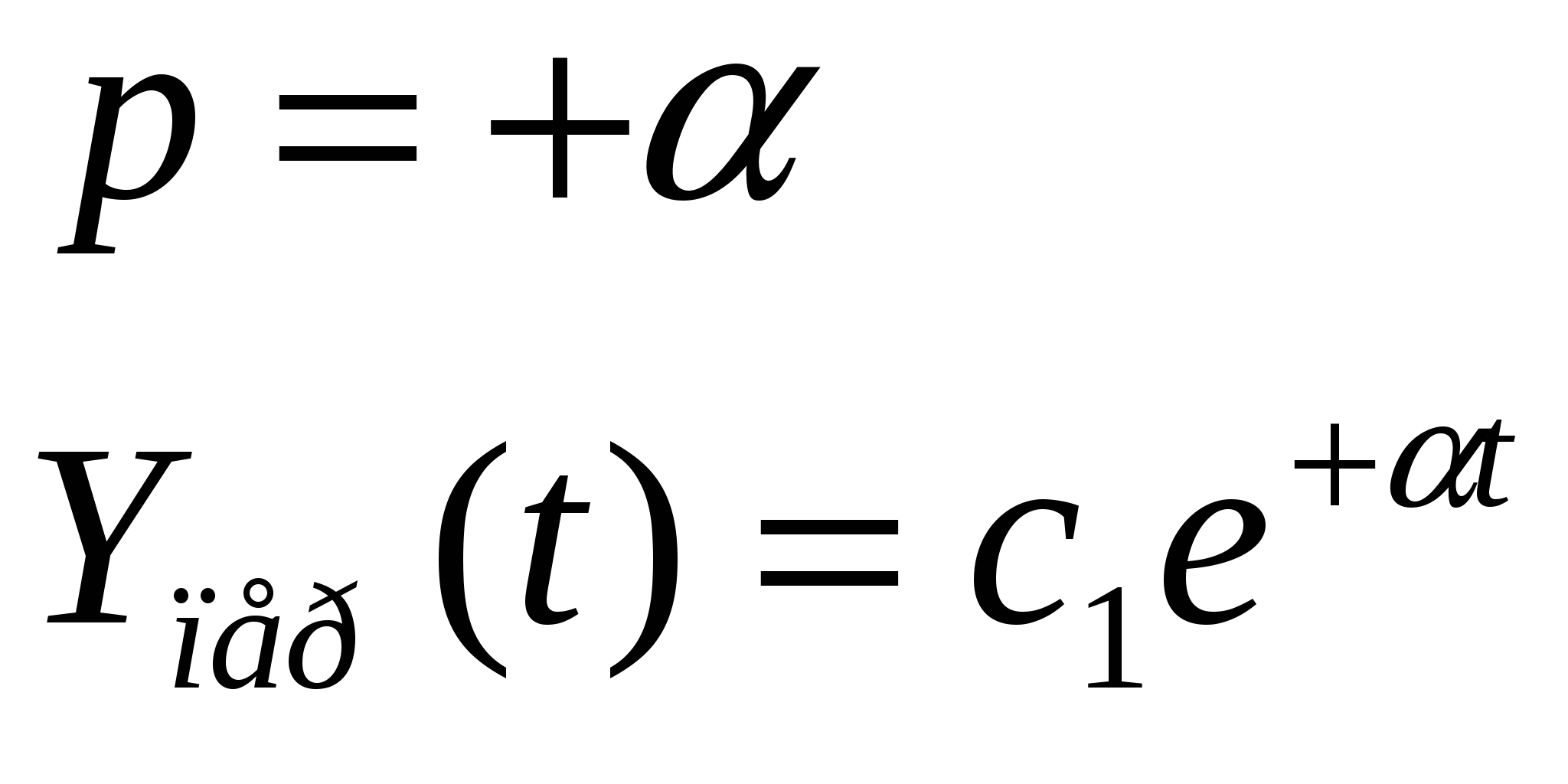 положительные вещественные корни положительные вещественные корни
незатухающий процесс
Неустойчивая система
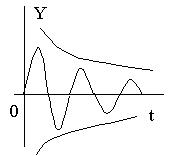
3) 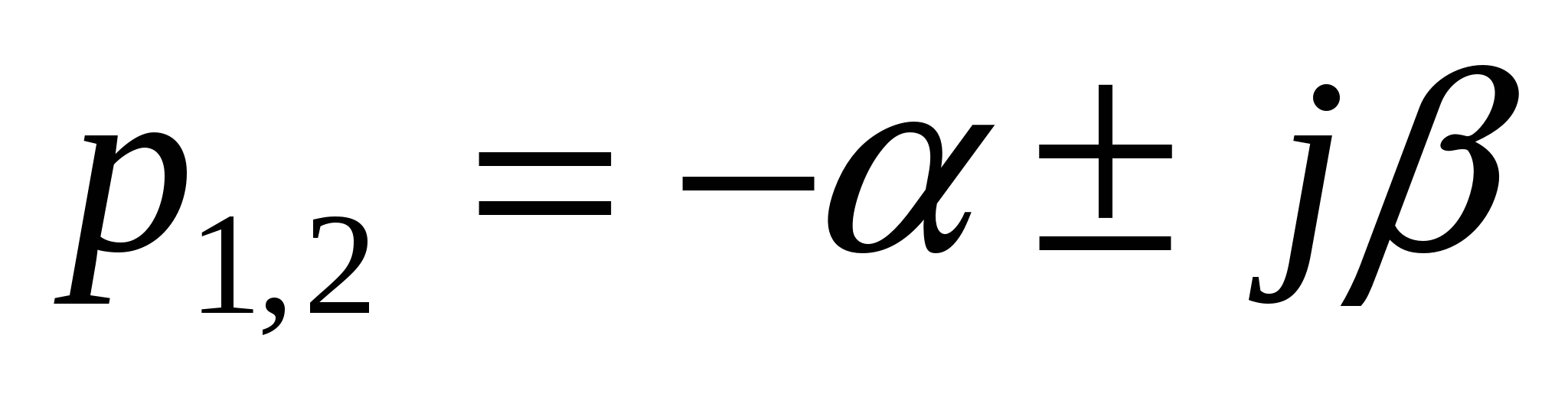 корни комплексно-сопряженные с корни комплексно-сопряженные с
отрицательной вещественной частью
з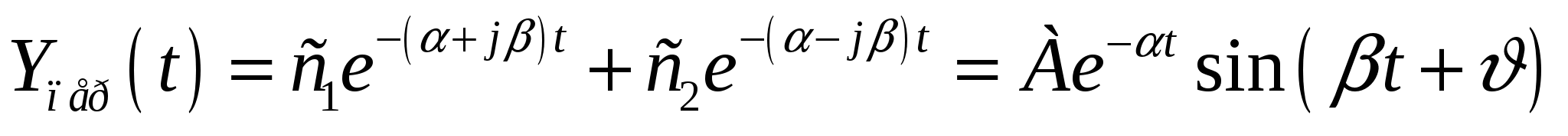
атухающие гармонические колебания
С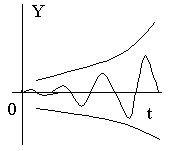 истема устойчива. истема устойчива.
4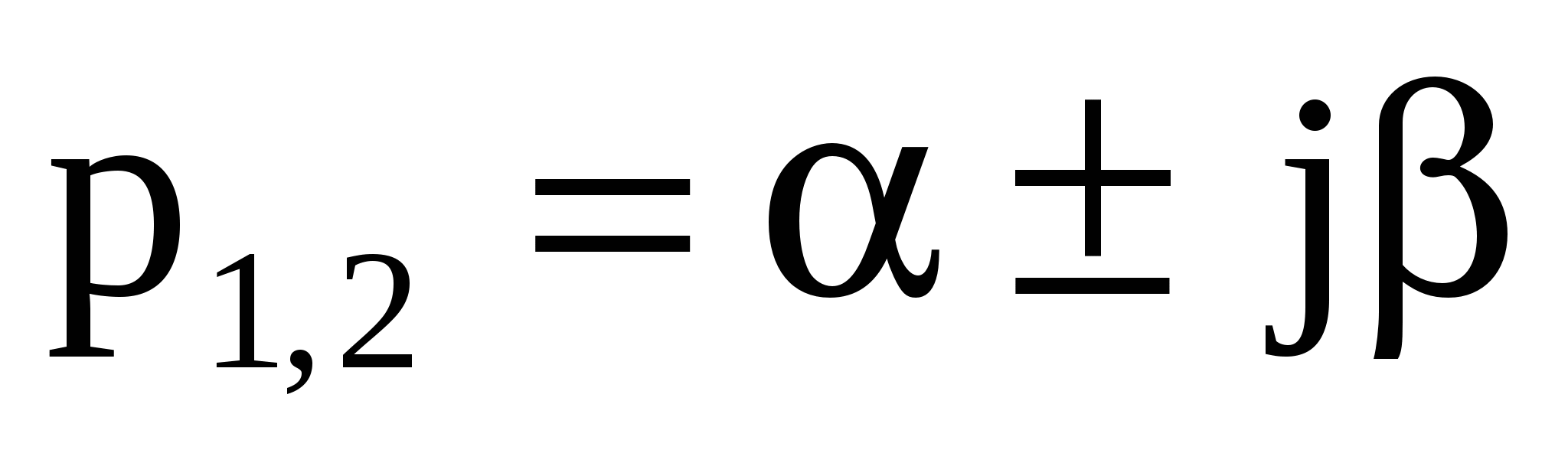 ) комплексно-сопряженные с положительной ) комплексно-сопряженные с положительной
вещественной частью
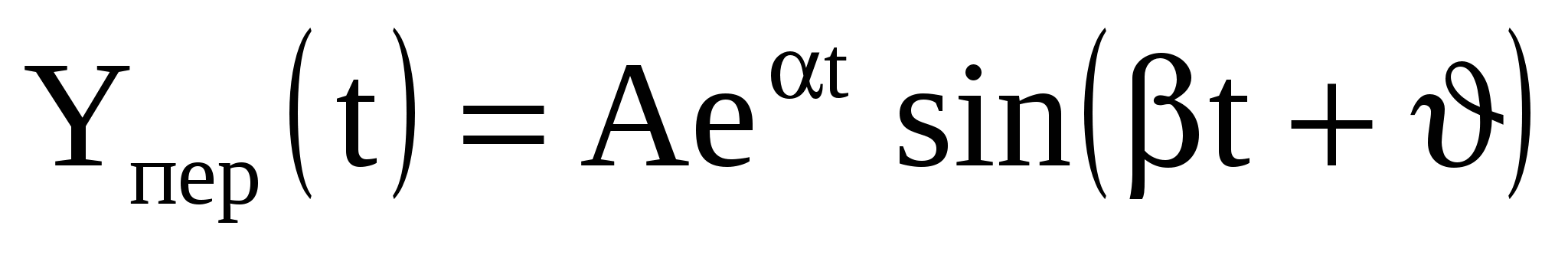 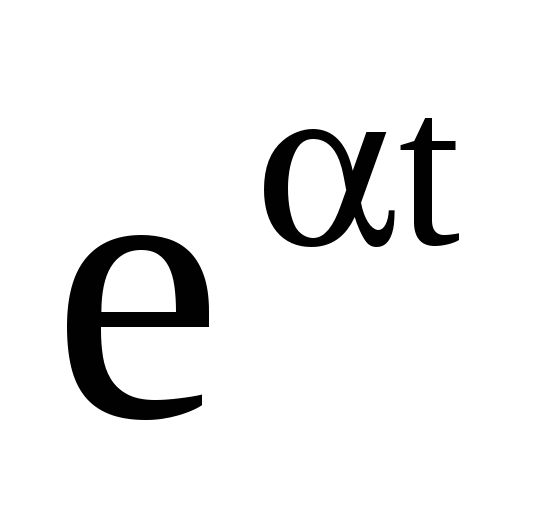
Неустойчивая система
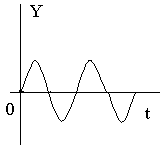
5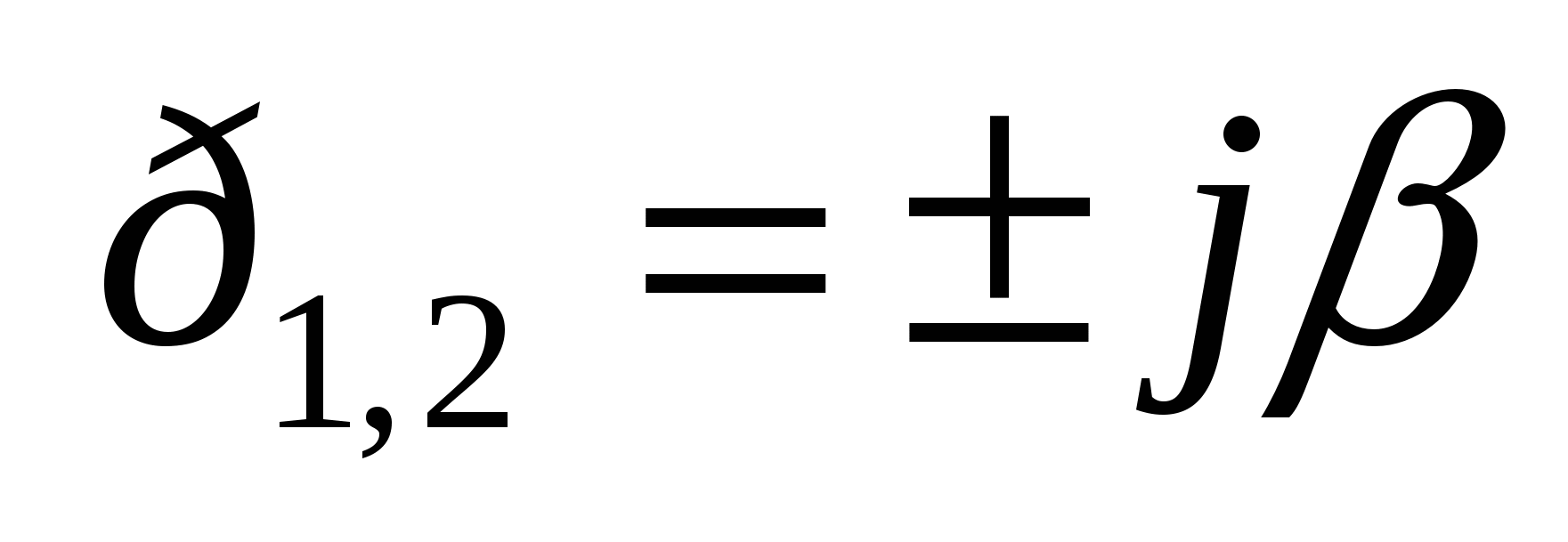 ) )  комплексные корни (чисто мнимые) комплексные корни (чисто мнимые)
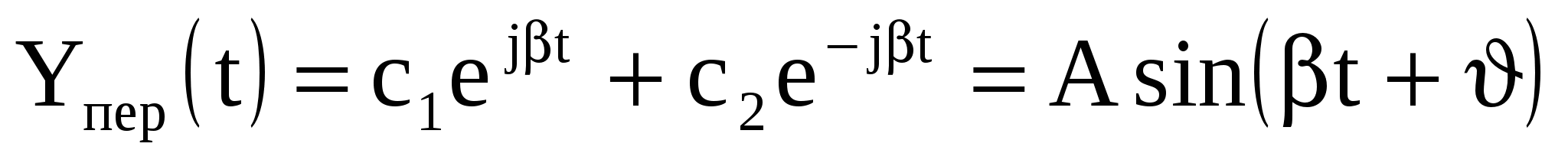
монотонный колебательный процесс
гармонические колебания
с постоянной частотой и амплитудой.
Система на границе устойчивости.
Вывод: Чтобы САУ была устойчивой необходимо, чтобы вещественные части корней были отрицательными. Если хотя бы один корень имеет положительную вещественную часть, то процесс будет расходящийся а система – неустойчива.
Если корень равен 0, то малейшее появление отрицательной составляющей сделает процесс устойчиво колебательным, а положительной – неустойчиво колебательным.
Часто корни характеристического уравнения при анализе устойчивости систем изображают на комплексной плоскости – плоскости корней характеристического уравнения
Комплексная плоскость мнимой осью разбивается на 2 части. Левую сторону называют областью устойчивости, а правую – областью неустойчивого движения.
Если корни лежат на мнимой оси или в 0, то система находится на границе устойчивости.
Вывод: Для устойчивости САУ необходимо и достаточно, чтобы все корни характеристического уравнения лежали слева от мнимой оси плоскости корней. Если хоть один корень справа, то система неустойчива. Таким образом, мнимая ось есть граница, за которую корни не должны переходить.
Если система имеет хотя бы один нулевой корень или хотя бы одну пару чисто мнимых корней, а все остальные корни имеют отрицательную вещественную часть, то система находится на границе устойчивости. При этом выделяют 3 типа границ устойчивости линейных систем:
1. Апериодическаяграница устойчивости, которая соответствует р=0. Когда корень – нуль, то в характеристическом уравнении и система будет устойчива относительно скорости изменения управляемой величины, а сама управляющая величина может принимать произвольное значение. Система является нейтрально устойчивой.
2. Колебательная граница устойчивости, которой соответствуют чисто мнимые корни
В связи с тем, что корни характеристического уравнения определять трудно для систем высокого порядка, были разработан целый ряд критериев, с помощью которых судят об устойчивости систем.
6.2. Алгебраические критерии.
6.2.1 Критерий устойчивости Гурвица.
При рассмотрении алгебраических критериев используются лишь коэффициенты характеристического уравнения и необходимые и достаточные условия устойчивости систем.
Необходимое условие является справедливым для всех систем:
Все коэффициенты характеристического уравнения должны быть положительными
Н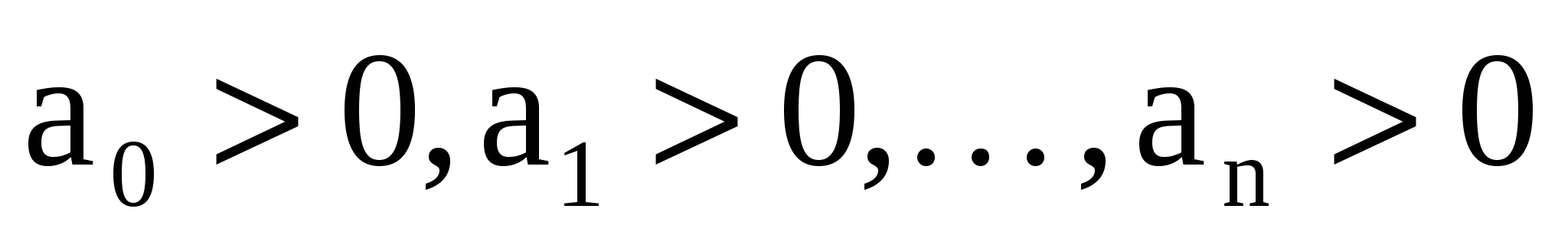 еобходимое условие является и достаточным для систем 1-го и 2-го порядка. еобходимое условие является и достаточным для систем 1-го и 2-го порядка.
Для устойчивости линейной САУ по критерию Гурвица необходимо и достаточно, чтобы были положительными n главных определителей матрицы коэффициентов характеристического уравнения заданной системы (знаменатель передаточной функции):

|
|
|
 Скачать 11.96 Mb.
Скачать 11.96 Mb. структуре обязательны датчики возмущения. Система описывается передаточной функцией разомкнутой системы: x(t) = g(t) - f(t).
структуре обязательны датчики возмущения. Система описывается передаточной функцией разомкнутой системы: x(t) = g(t) - f(t). истема описывается передаточной функцией разомкнутой системы и уравнением замыкания: x(t) = g(t) - y(t) Woc(t). Алгоритм работы системы заключен в стремлении свести ошибку x(t) к нулю.
истема описывается передаточной функцией разомкнутой системы и уравнением замыкания: x(t) = g(t) - y(t) Woc(t). Алгоритм работы системы заключен в стремлении свести ошибку x(t) к нулю.
 омбинированное управление
омбинированное управление лгебраические
лгебраические )
) 
 истема устойчива.
истема устойчива.