Краткая теория для выполнения лабораторных работ по курсу оту
 Скачать 11.96 Mb. Скачать 11.96 Mb.
|
Матрица коэффициентовПо диагонали от левого верхнего угла до правого нижнего выписывают все коэффициенты по порядку от а1 до аn. Каждая строка дополняется коэффициентами с возрастающими индексами слева направо так, чтобы чередовались строки с чётными и нечётными индексами. В случае отсутствия даннного коэффициента или если его индекс <0 или >n, то на его место пишется 0.   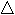 а1 а3 а5 ………0 1=а1>0 а1 а3 а5 ………0 1=а1>0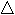   а0 а2 а4 ………0 а1 а3 а0 а2 а4 ………0 а1 а3
… 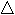  ……………. а1 а3 а5 ……………. а1 а3 а5……………..аn 3= а0 а2 а4
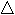  ………………… …………………n =аn* n-1 Если аn=0 , то имеет место апериодическая граница устойчивости. Е  сли n1=0, то это колебательная граница устойчивости. сли n1=0, то это колебательная граница устойчивости.6.2.2 Критерий Раусса. Так же базируется на коэффициентах характеристического уравнения, из которого строится таблица. Д  ля устойчивости систем по критерию Раусса необходимо и достаточно чтобы при а0>0 все коэффициенты первого столбца таблицы Раусса были положительными. ля устойчивости систем по критерию Раусса необходимо и достаточно чтобы при а0>0 все коэффициенты первого столбца таблицы Раусса были положительными.
b2=(a1*a4-a0*a5)/a1 b3=(a1*a6-a0*a7)/a1 b4=(a1*a8-a0*a9)/a1 c1=(b1*a3-a1*b2)/b1 c2=(b1*a5-a1*b3)/b1…… Для устойчивости системы все коэффициенты 1-го столбца должны быть больше 0 а0>0, a1>0… 6.3. Частотные критерии6.3.1 Критерий Михайлова. Критерий базируется на поведении кривой, которую описывает конец вектора (X(ω),Y(ω)) замкнутой системы при изменении частоты от 0 до + Возьмём характеристический полином следующего вида: Подставим в него Изобразим годограф Михайлова выражения 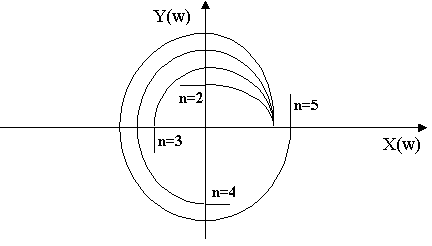 Берём значения Формулировка критерия Михайлова. Чтобы САР была устойчивой, необходимо и достаточно, чтобы вектор D(jω) при изменении частоты от 0 до +∞ начал движение с точки, лежащей на положительной вещественной оси, и, вращаясь только против часовой стрелки и нигде не обращаясь в нуль, прошел последовательно n квадрантов комплексной плоскости, повернувшись на угол n∙π/2, где n – степень характеристического уравнения D(jω)=0 Другими словами, требуется, чтобы кривая Михайлова проходила последовательно 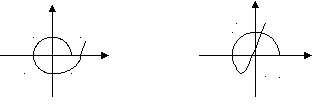 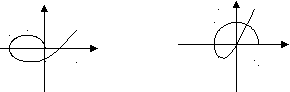 Устойчивая Неустойчивая Апериодическая Колебательная граница устойчивости граница устойчивости Другая формулировка критерия Михайлова: Она состоит в использовании свойства перемежаемости корней многочленов Идя по кривой Михайлова от т. Это значит, что корни уравнений Кривые 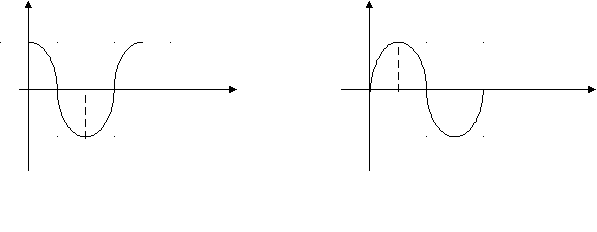 Перемежаться должны корни Условием устойчивости системы является перемежаемость корней полиномов вещественной и мнимой частей комплексной передаточной функции. Нарушение этого условия говорит о неустойчивости системы. 6.3.2 Критерий устойчивости Найквиста. Данный критерий относится к частотным критериям. Как и критерий Михайлова, критерий Найквиста базируется на АФЧХ разомкнутой системы и даёт правила, согласно которым, по виду АФЧХ разомкнутой системы можно судить об устойчивости замкнутой системы. Соответственно существует две формулировки критерия Найквиста, в зависимости от поведения системы в разомкнутом состоянии. а) система устойчива в разомкнутом состоянии Правило: Если разомкнутая САУ устойчива, то для устойчивости замкнутой системы необходимо и достаточно. Чтобы АФЧХ разомкнутой системы не охватывала точку с координатами Пусть передаточная функция разомкнутой системы такова: 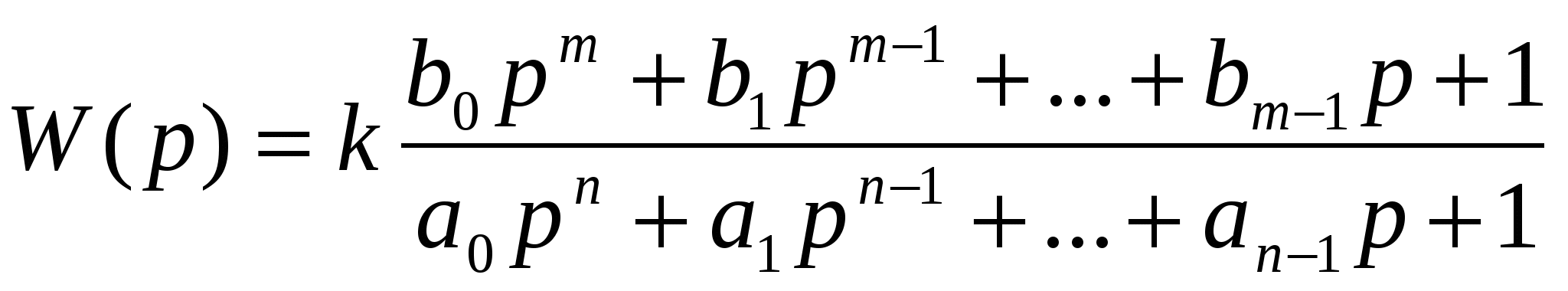 , , 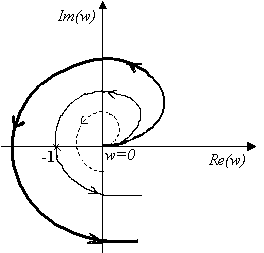 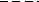 Абсолютная учтойчивость Абсолютная учтойчивость   Система на границе устойчивости Система на границе устойчивости  Неустойчива Неустойчиваб) система с неустойчивой разомкнутой цепью Пусть х.у. разомкнутой системы имеет Д 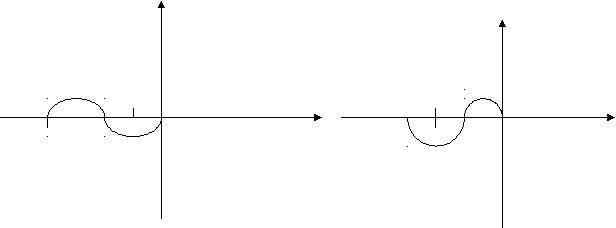 ругими словами, АФЧХ разомкнутой системы может пересекать ось абсцисс левее точки ругими словами, АФЧХ разомкнутой системы может пересекать ось абсцисс левее точки Положительный переход – сверху вних, отрицательный – снизу вверх. 6.4. Использование ЛАЧХ. Логарифмические критерии устойчивости являются следствием критерия Найквиста, поэтому так же позволяют судить об устойчивости замкнутой системы управления по логарифмическим частотным характеристикам разомкнутой системы. Следовательно, здесь так же рассматриваются два случая: а) если САР в разомкнутом состоянии устойчива 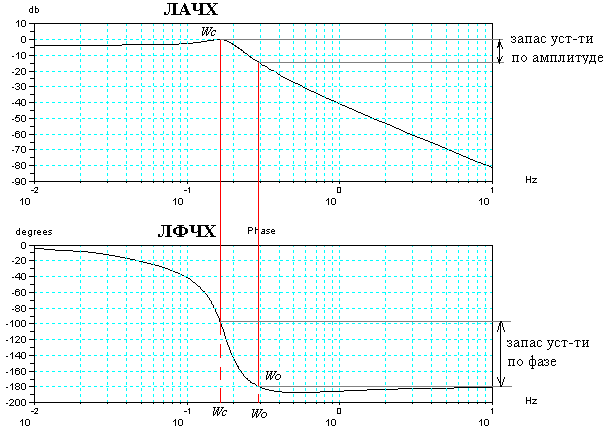 Для устойчивости замкнутой САР необходимо и достаточно, чтобы точка пересечения фазовой характеристики разомкнутой системы с линией Запас устойчивости по модулю ∆L показывает, насколько может измениться модуль АФЧХ для выхода системы на границу устойчивости при неизменных фазовых соотношениях. Запас устойчивости по фазе ∆φ показывает, насколько должна измениться фаза каждого вектора АФЧХ для выхода системы на границу устойчивости при неизменных их модулях. Требования к запасу устойчивости по амплитуде ≥8 -10 дБ, по фазе – ≥30 - 35º. б) если САР в разомкнутом состоянии не устойчива 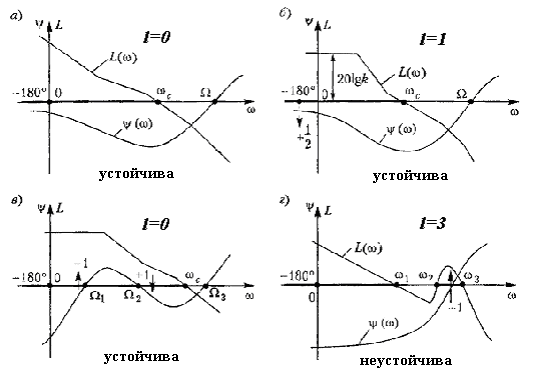 Для устойчивости замкнутой САР необходимо и достаточно, чтобы сумма переходов логарифмической фазовой характеристики разомкнутой системы через критический отрезок была равна l/2, где l – число корней с положительной вещественной частью в знаменателе передаточной функции разомкнутой системы W(p). Критическим отрезком называется область с положительным значением ЛАЧХ, сложные системы могут иметь два и более критических отрезков. Переход сверху вниз считается положительным (+1), снизу вверх – отрицательным (-1), если фазовая характеристика начинается на оси -180º и идет вниз, то переход равен +1/2, если вверх, то –1/2. а) ЛФЧХ не пересекает критический отрезок, l=0, следовательно замкнутая система усойчива; б) в данном случае система устойчива, так как при l=1, имеется +1/2 перехода через критический отрезок на частоте ω=0; в) здесь имеется +1 переход на частоте Ω2 и –1 переход на частоте Ω1, замкнутая система устойчива так как l=0 и сумма переходов равна нулю; г) показан случай, когда критический отрезок состоит из двух частей, одна его часть находится на частотах ω≤ω1, а другая на частотах ω2≤ω≤ω3, так как имеется –1 переход при l=3, то замкнутая система неустойчива. |

 1 а3 а5…....0 2= а0 а2
1 а3 а5…....0 2= а0 а2