Краткая теория для выполнения лабораторных работ по курсу оту
 Скачать 11.96 Mb. Скачать 11.96 Mb.
|
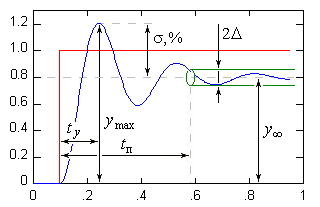
7. Качество процессов автоматического управления.САУ характеризуются не только устойчивостью, но и другими динамическими характеристиками или свойствами. К таким динамическим свойствам относятся:
Если при рассмотрении устойчивости линейных систем было определено, что устойчивость не зависит от входных воздействий, а определяется только параметрами системы, то при исследовании качества вид входного воздействия и его амплитудное значение имеют существенное значение. Все методы анализа качества переходного процесса можно разделить на две группы: 1. Прямые методы – это непосредственное решение дифференциальных уравнений, которые описывают систему и выполнение графического построения переходного процесса. Эти методы наиболее точны и находят все более широкое применение. Прямые показатели качества оценивают по переходным характеристикам. При этом прямые показатели качества делят на: Основные: 1. Вид переходной характеристики.(колебательная, амплитудная и т. д.) 2. Время переходного процесса( 3. Величина наибольшего отклонения в переходном процессе – перерегулирование.( 4. Величина допустимой установившейся ошибки(∆, % от y∞). 5. Колебательность переходного процесса, характеризуется числом колебаний за время регулирования. Вспомогательные:
 2. Косвенные методы позволяют обойти непосредственное решение уравнений, описывающих систему. Применяют обычно следующие косвенные методы:
Сущностью косвенных методов является:
Замена точного управления приближенным является наиболее частым способом при косвенной оценке качества. Такая аналитическая аппроксимация может быть применена предварительно к ПФ. По виду переходных процессов можно определить следующие показатели качества: 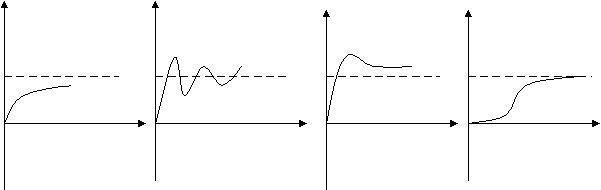 1 Монотонный Колебательный Апериодический S- образный Это группа процессов статических объектов. В динамических объектах: 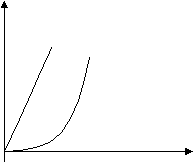 1 - идеально интегрирующее звено 2 - реально интегрирующее звено 1 2 Основным показателем качества систем является установившаяся(статическая) ошибка. Допустимое значение статической ошибки ( 8. Синтез САР. Регуляторы. Под синтезом САР понимают работу по расчету ее рациональной структуры и оптимальных параметров отдельных элементов. При решении задачи синтеза часть структуры системы, например, объект управления, регулирующие органы, средства измерения и т.д., известны. Неизвестной является регулирующая часть САР. Задачей математического синтеза является определение оптимального, т.е. наилучшего в данных условиях, алгоритма или закона регулирования. Для большинства используемых в тепловой автоматике САР структура и алгоритмы регулирования известны. Например, САР уровня жидкости, так называемый трехимпульсный регулятор, реализующий пропорционально-интегральный закон, обеспечивает требуемое качество регулирования. В этом случае задача синтеза сводится к расчету параметров этого регулятора на основе характеристик конкретного объекта, регулирующих органов и т.д. Такую задачу часто называют инженерным синтезом. Задачу инженерного синтеза можно считать завершенной, если расчет качества ожидаемого переходного процесса удовлетворяет требованиям к системе. Не исключены случаи, когда в рамках выбранной структуры это сделать не удается. Тогда приходится использовать дополнительные сигналы, например, возмущениия производимые от отклонения, использовать местные обратные связи, вводить корректирующие устройства. Имея в наличии структуру, алгоритм и его численные параметры, можно решать третью задачу – техническую реализацию. В подавляющем большинстве случаев регулятор регулятор собирается из стандартных блоков, поэтому под синтезом понимают более узкую задачу – расчет корректирующих устройств САР. ПИД-регулятор 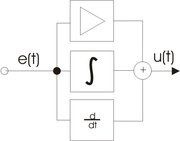 Схема, иллюстрирующая принцип работы ПИД-регулятора Пропорционально-интегрально-дифференциальный (ПИД) регулятор — устройство в цепи обратной связи, используемое в системах автоматического управления для поддержания заданного значения измеряемого параметра. ПИД-регулятор измеряет отклонение стабилизируемой величины от заданного значения (уставки) и выдаёт управляющий сигнал, являющийся суммой трёх слагаемых, первое из которых пропорционально этому отклонению, второе пропорционально интегралу отклонения и третье пропорционально производной отклонения (или, что то же самое, производной измеряемой величины). Если какие-то из составляющих не используются, то регулятор называют пропорционально-интегральным, пропорционально-дифференциальным, пропорциональным и т. п. Общие сведения Пропорциональная составляющая Пропорциональная составляющая вырабатывает выходной сигнал, противодействующий отклонению регулируемой величины от заданного значения, наблюдаемому в данный момент времени. Он тем больше, чем больше это отклонение. Если входной сигнал равен уставке, то выходной равен нулю. Однако при использовании только пропорционального регулятора значение регулируемой величины никогда не стабилизируется на заданном значении. Существует так называемая статическая ошибка, которая равна такому отклонению регулируемой величины, которое обеспечивает выходной сигнал, стабилизирующий выходную величину именно на этом значении. Например, в регуляторе температуры выходной сигнал (мощность нагревателя) постепенно уменьшается при приближении температуры к уставке, и система стабилизируется при мощности равной тепловым потерям. Температура не может достичь уставки, так как в этом случае мощность нагревателя станет равна нулю, и он начнёт остывать. Чем больше коэффициент пропорциональности между входным и выходным сигналом (коэффициент усиления), тем меньше статическая ошибка, однако при слишком большом коэффициенте усиления могут начаться автоколебания, а при дальнейшем увеличении коэффициента система может потерять устойчивость. Интегральная составляющая Для устранения статической ошибки используют интегральную составляющую. Она позволяет регулятору «учиться» на предыдущем опыте. Если система не испытывает внешних возмущений, то через некоторое время регулируемая величина стабилизируется на заданном значении, сигнал пропорциональной составляющей будет равен нулю, а выходной сигнал будет полностью обеспечивать интегральная составляющая. Дифференциальная составляющая Дифференциальная составляющая противодействует предполагаемым отклонениям регулируемой величины, которые могут произойти в будущем. Эти отклонения могут быть вызваны внешними возмущениями или запаздыванием воздействия регулятора на систему. Чем быстрее регулируемая величина отклоняется от уставки, тем сильнее противодействие, создаваемое дифференциальной составляющей. Теория Назначение ПИД-регулятора — в поддержании заданного значения x0 некоторой величины xс помощью изменения другой величины u. Значение x0 называется уставкой, а разность e = (x0 − x) — невязкой или рассогласованием. Выходной сигнал регулятора u определяется тремя слагаемыми: 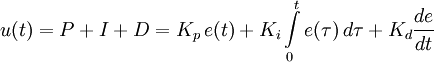 где Кp, Кi, Кd — коэффициенты усиления пропорциональной, интегральной и дифференциальной составляющих регулятора, соответственно. Большинство методов настройки ПИД-регуляторов используют несколько иную формулу для выходного сигнала, в которой на пропорциональный коэффициент усиления умножены также интегральная и дифференциальная составляющие: 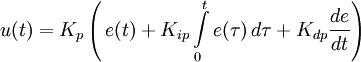 Часто в качестве параметров ПИД-регулятора используются: относительный диапазон постоянные интегрирования и дифференцирования, имеющие размерность времени Следует учитывать, что термины используются по-разному в различных источниках и разными производителями регуляторов. 9. Краткие сведения о программном комплексе VisSim. VisSim (визуальный симулятор) это программа моделирования технических и физических объектов и систем, разработанная и развиваемая компанией Visual Solutions. Программа позволяет, используя развитой графический интерфейс, легко, как из кубиков, строить, а затем и исследовать модели систем широкого диапазона сложности. При использовании VisSim'а не требуется владеть программированием на языках высокого уровня или ассемблере. В то же время, владеющие программированием могут создавать собственные блоки, дополняя ими богатую библиотеку стандартных блоков VisSim'а. Студенческая версия программы распространяется бесплатно, правда имеет ряд ограничений и более скромные возможности, по сравнению с профессиональными версиями. Диаграмма VisSim'а - виртуальная модель Диаграммой в VisSim называется совокупность блоков и надписей, помещенных на рабочее пространство, способных функционировать при запуске процесса моделирования. Диаграмма может быть сохранена в виде отдельного файла и, при необходимости, открыта вновь. В диаграмму VisSim'а в принципе могут быть включены, с помощью дополнительных компьютерных плат, и внешние физические устройства, которыми VisSim сможет управлять. 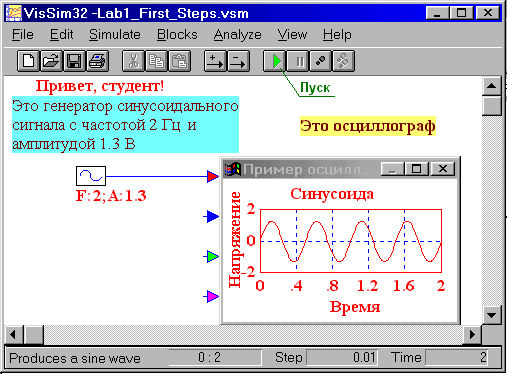 Рис.1 Пример простой VisSim – диаграммы. Модели систем и объектов в программе VisSim строятся из отдельных элементов – т.н. блоков. Блок это виртуальный аналог физического элемента реальной системы. Взаимодействие между блоками моделируется сигналами – функциями времени. Виртуальные блоки VisSim’а могут иметь или вход, на который может быть подан выходной сигнал другого блока, или выход, виртуальный сигнал с которого может быть подан на вход другого блока, или и вход, и выход одновременно. Внешне, для исследователя, виртуальные блоки VisSim реагируют на входные сигналы точно так же, как реальные устройства на реальные воздействия. Сигналы в модели могут быть измерены с помощью индикаторных блоков или рассмотрены и изучены с помощью виртуального осциллографа. Блоки VisSim’а можно условно разделить на три основных категории и одну дополнительную:
Важным компонентом модели является соединительная линия – виртуальный аналог физического соединения элементов, передающего воздействия от одного элемента к другому. В VisSim'е соединительные линии однонаправленные, передают сигналы только в одном направлении. Это требует при создании модели разделять моделируемую систему на элементы соответствующим образом. Примечание: Входные и выходные сигналы могут быть как одиночными функциями времени, так и набором таких функций. В последнем случае сигнал называется векторным, как и соответствующий вход или выход блока. Блоки, имеющие только выход: генераторы Примерами таких блоков являются блоки:
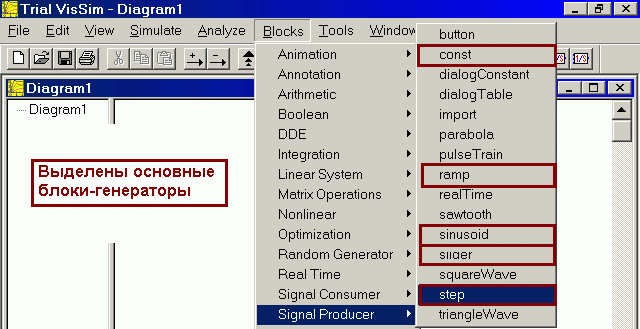 Рис.2 Важные блоки-генераторы программы VisSim. Для помещения блока на рабочее пространство следует щелкнуть по соответствующему пункту меню, перевести курсор в нужное место рабочего пространства и щелкнуть левой клавишей мыши. Блоки, имеющие вход и выход: преобразователи. Важнейшие блоки для моделирования линейных систем:
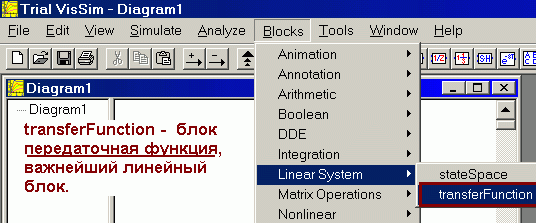 Рис.3 Меню для вызова линейного блока общего вида передаточная функция (transferFunction). Сумматор и усилитель вызываются: Blocks Arithmetic summingJunction или gain. Блоки, имеющие только вход: индикаторы. Важнейшими индикаторами являются блоки:
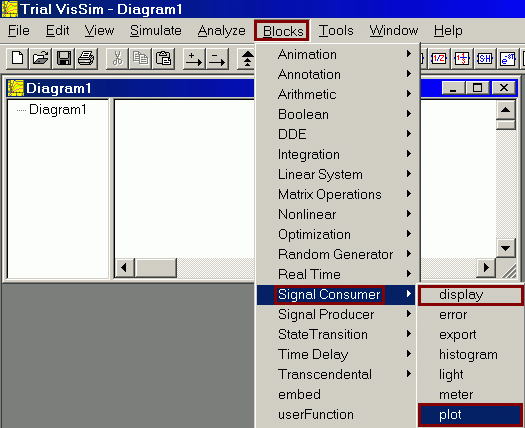 Рис.4 Меню для вызова блоков plot (осциллограф) и display (цифровой индикатор) – важнейших виртуальных измерительных приборов программы VisSim. Блоки без входов и выходов: надписи и комментарии. Эти блоки позволяют создавать на рабочем пространстве диаграммы VisSim текстовые области, которые помогают понять смысл диаграммы и содержат сведения о том, кто, когда и какую диаграмму создал. Основной блок: label – надпись (Blocks - Annotation - label). Построение структурной схемы После того, как на рабочее поле помещены все необходимые блоки, необходимо задать их параметры. Для этого необходима дважды щелкнуть по данному блоку и в появившемся окне указать нужные значения. Например, для блока передаточной функции: 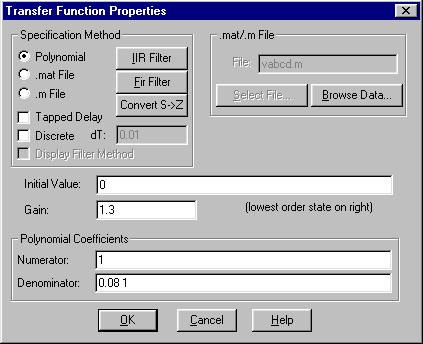 Передаточная функция указывается в виде отношения двух полиномов: числителя (Numerator) и знаменателя (Denominator). Полиномы задаются с помощью коэфициентов, которые записываются по порядку через пробел, начиная со старшей степени, если какой-либо из коэффициентов отсутствует на его месте пишется ноль. Усиление (Gain) равно 1.3 выноситься перед дробью. Запуск модели и подбор параметров моделирования Щелкнуть по кнопке Пуск с зеленым треугольником на панели инструментов VisSim. Процесс моделирования запущен. В результате на осциллографе будет построена переходная функция. 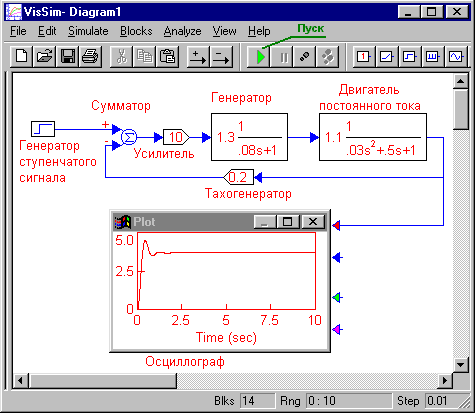 Поскольку большую часть времени развертки осциллографа, длительность которой по умолчанию составляет 10 сек, переходная характеристика постоянна, то для более подробного ее рассмотрения изменим время, т.е. продолжительность моделирования. Для этого в меню VisSim выберем Simulate (моделирование) – Simulation Properties (свойства моделирования) и в появившемся окне диалога на вкладке Range (Диапазон) заменим параметр End: 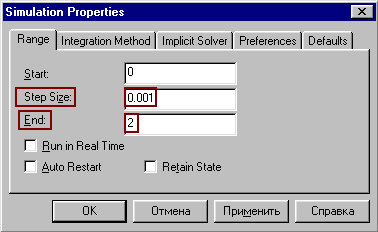 Наконец добавим сетку координат и надпись в заголовке окна осциллографа. Для этого следует дважды щелкнуть по окну осциллографа и в появившемся диалоговом окне на вкладке Options (параметры) щелчком поставить галочку в квадратике Grid Lines: 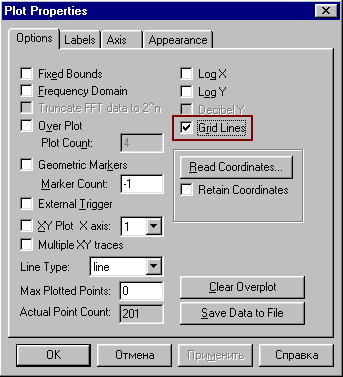 На вкладке Labels, в графе Title (заголовок) написать Переходная характеристика. Здесь, так же, можно сделать подписи осей и единиц измерения. Построение ЛАЧХ и ЛФЧХ. Порядок построения ЛАЧХ и ЛФЧХ в программе VisSim следующий.
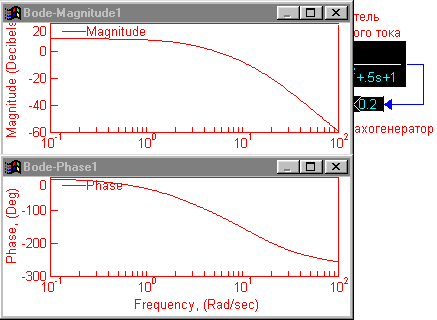
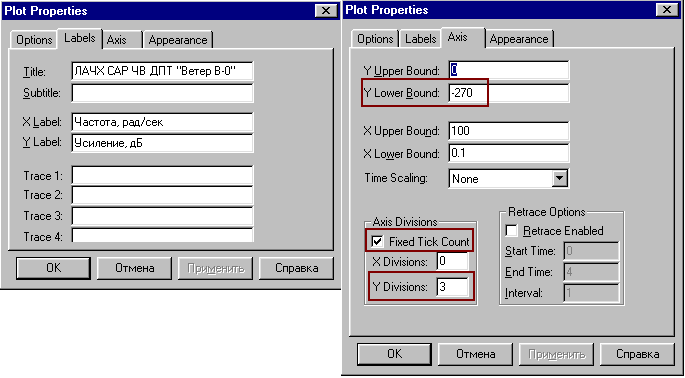 В результате ЛАЧХ и ЛФЧХ примут вид: 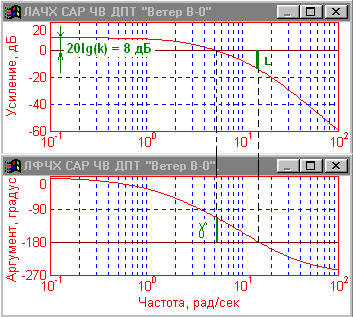 Примечание. Для изменения частотного диапазона, в котором строится ЛАЧХ, необходимо выбрать Analyze - Frequency Range, и установить начальное и конечное значения частотного диапазона. Например, Start - 0.001, End 10, число шагов Step Count 200. Отметим, что большое число декад снижает точность определения значений по ЛАЧХ. |
