Давыдков_физика_Ч. 2. Давыдков_физика_Ч. Курс лекций по общей физике предназначен для студентов института дистанционного образования, изучающих вторую часть курса физики

• Название: Курс лекций по общей физике предназначен для студентов института дистанционного образования, изучающих вторую часть курса физики
• Анкор: Давыдков_физика_Ч. 2.doc
• Дата: 27.02.2018
• Размер: 2.62 Mb.
• Имя файла: Давыдков_физика_Ч. 2.doc
• Тип: Курс лекций; #15985
• страница: 9 из 15

1.16. Поле в однородном диэлектрике

Необходимо отметить ещё одну важную особенность про-цесса поляризации.

Под действием внешнего поля положительные и отри-цательные заряды в диэлектрике смещаются. В результате молекулы диэлектрика ориентированы примерно так, как показано на рисунке.

Внутри диэлектрика рядом с положительным зарядом диполя распо-лагается отрицательный заряд соседней молекулы.

Поскольку молекулы одинаковые, то сумма этих зарядов равна нулю. Другими словами – заряды диполей внутри диэлектрика взаимно компенсируются.

Из рисунка видно, что на поверхности диэлектрика такая компенсация отсутствует – снаружи нет диполей, способных вызвать компенсацию. Поэтому на противоположных поверх-ностях диэлектрика во внешнем электрическом поле возникают нескомпенсированные заряды.

Молекулы твёрдого вещества не могут свободно изменять своё положение. Следовательно, нескомпенсированные заряды диполей не могут перемещаться внутри объёма или по поверхности диэлектрика. Поэтому их называют связанными.

Связанные заряды, так же как и любые заряды, создают электрическое поле.

Это дополнительное электрическое поле всегда направлено против внешнего поля (это видно из рисунка). Поэтому электрическое поле внутри диэлектрика всегда слабее, чем вне его:

Е = Е_о–
где Е – напряжённость электрического поля внутри диэлектрика, Е – напряжённость поля связанных зарядов, Е_о – напряжённость поля, созданного внешними зарядами.


В соответствии с теоремой Гаусса, напряжённость поля связанных зарядов внутри диэлектрика*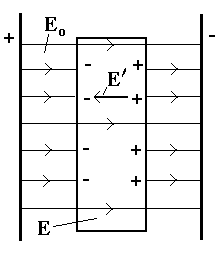




,

где  – поверхностная плот-ность связанных зарядов.

Поверхностную плотность связанных зарядов  можно найти из следующих соображе-ний.

В соответствии с опреде-лением поляризованности ди-электрика P полный дипольный электрический момент пласти-ны

р = Р^.V.

Объём прямоугольной пластины V = S^.d (d – толщина плас-тины), поэтому

р = Р^. S^.d.

С другой стороны, полный дипольный электрический момент пластины

р = qd,

где q – полный связанный заряд боковой грани пластины, величина которого q = S. Поэтому

р = Sd,

и это означает, что

Р = ,

т. е. поляризованность диэлектрика оказывается равной по-верхностной плотности связанных зарядов.

Ранее было получено, что поляризованность Р = _оЕ, следовательно, теперь можно записать

 = _оЕ.

________________________
* Это поле, созданное двумя бесконечными равномерно заряженными плос-костями.

Учитывая, что , для величины напряженности электрического поля внутри диэлектрика получаем
Е = Е_о – Е,

,

где  = 1 +  – диэлектрическая проницаемость вещества.

Диэлектрическая проницаемость является безразмерной величиной и показывает, во сколько раз электрическое поле внутри диэлектрика слабее внешнего.

В изотропных средах диэлектрическая проницаемость является скалярной величиной.

17. Вектор электрического смещения.

Теорема Гаусса для поля в диэлектрике

Уменьшение напряжённости электрического поля на поверх-ности диэлектрика происходит скачком (поскольку именно на поверхности расположены связанные заряды), что вызывает некоторые сложности при расчётах электрических полей в веществе.

Например, если пространство заполнено несколькими слоями разных диэлектриков, то даже в самой простой ситуации расчёт будет довольно сложным, так как из-за связанных зарядов в каждом слое будет своя напряжённость электрического поля.

Поэтому необходима такая характеристика электрического поля, которая не зависит от связанных зарядов. Чтобы получить такую характеристику, поступим следующим образом.

Как уже отмечалось, напряжённость поля внутри диэлектрика Е = Е_о – Е, где Е – напряжённость поля связанных зарядов, равная _о.

Напряжённость внешнего электрического поля, созданного свободными зарядами двух параллельных бесконечных прово-дящих плоскостей, можно выразить как Е = _своб_о.

Тогда напряжённость электрического поля внутри ди-электрика

.

Поскольку  = Р,

.

Тогда



или

_оЕ + Р = _своб.
Таким образом, величина _оЕ + Р не зависит от наличия связанных зарядов. Эту величину называют электрическим смещением.

Определение электрического смещения можно записать в векторной форме



или, поскольку Р = _оЕ,

.

Вектор электрического смещения в изотропных диэлектриках совпадает по направлению с вектором напряжённости электри-ческого поля внутри диэлектрика, так как в изотропных диэлектриках диэлектрическая проницаемость  является скаляр-ной величиной*.

Размерность вектора электрического смещения [D] = Кл/м².

Электрическое смещение является вспомогательной характе-ристикой электрического поля, зависящей только от свободных зарядов.

Таким образом, получена характеристика электрического поля, не зависящая от связанных зарядов. Использование такой характеристики даёт очевидные преимущества. Действительно, используя электрическое смещение, можно рассчитать электрическое поле (значение вектора D) как внутри диэлектрика, так и вне его, учитывая только свободные заряды. После этого легко найти напряжённость электрического поля в любой точке,


______________________________
* В анизотропных диэлектриках диэлектрическая проницаемость является тензорной величиной и, в общем случае, D и Е по направлению не совпадают.

просто поделив значение D в этой точке на значение ди-электрической проницаемости  в этой точке и на электрическую постоянную _о.

Рассчитывать электрическое поле в пространстве с ди-электриком можно с помощью теоремы Гаусса. Применительно к электрическому смещению она в любой среде имеет вид



и может быть прочитана следующим образом: поток вектора электрического смещения через замкнутую поверхность ра-вен сумме свободных зарядов, охваченных этой поверх-ностью *. Знать, каковы по величине связанные заряды и как они распределены в пространстве, в этом случае не нужно.