Давыдков_физика_Ч. 2. Давыдков_физика_Ч. Курс лекций по общей физике предназначен для студентов института дистанционного образования, изучающих вторую часть курса физики
 Скачать 2.62 Mb.
|
1.18. Условия на границе раздела двух диэлектриковРассмотрим границу раздела двух изотропных диэлектриков с диэлектрическими проницаемостями 1 и 2 (1 < 2). Пусть на границе раздела свободные заряды отсутствуют. Оба диэлектрика находятся в однородном электрическом поле напряжённостью Е. Напряжённость электрического поля в одном из диэлектриков будет равна Е1, во втором – Е2. 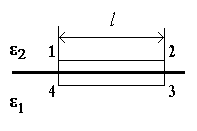 Выберем некоторый контур, охватывающий границу раздела двух сред. Поскольку электрическое поле консервативно, работа куло-новских сил на замкнутом конту-ре Al равна нулю Al = A12 + A23+ A34+ A41=0. На участках 12 и 34 рассматриваемого контура работа   ._____________________________ * В случае использования вектора напряженности теорема Гаусса имеет вид  В этих выражениях Е1 и Е2 – проекции векторов Е1 и Е2 на ось, параллельную границе раздела двух диэлектриков. Пусть l23 = l41 0. Тогда работа кулоновских сил на этих участках будет равна нулю. Тогда работа кулоновских сил на всей длине контура Al = A12 +A34 = 0 и A12 = -A34. Последнее соотношение можно переписать в виде  .Сократив одинаковые множители, получаем  .Таким образом, компонента вектора напряжённости, парал-лельная границе раздела двух сред (тангенциальная компонента), с обеих сторон от границы одинакова. Вектор электрического смещения D = oE. Следовательно, D1 = o1E1, D2 = o2E2, А это, в свою очередь, означает, что  или  .Другими словами – тангенциальная компонента вектора (D) на границе раздела скачкообразно изменяется в соответствии с последним соотношением. Т 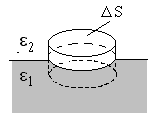 еперь рассмотрим поведение компонент векторов D и E, перпендикулярных границе раз-дела двух диэлектриков. Для этого воспользуемся теоремой Гаусса. В качестве поверхности интегрирования выберем цилиндр бесконечно малой высоты, основания которого параллельны границе раздела двух диэлектриков.В соответствии с теоремой Гаусса, считая электрическое поле однородным, мы вправе записать*:  и  .Отсюда следует, что  .Таким образом, на границе раздела скачком изменяется нормальная составляющая вектора напряжённости и не изменя-ется нормальная составляющая вектора электрического смещения. Вследствие этого силовые линии на границе раздела двух диэлектриков изменяют направление**. Действительно, Е1 = Е2, 1Е1n = 2Е2n. И 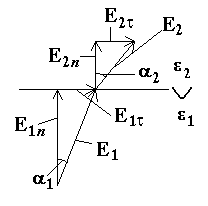 з рисунка видно, что  . Выражая тангенс угла наклона силовых линий в каждом из диэлектриков, получим: ,  , .Таким образом, в среде с бóль-шей диэлектрической проницаемостью (2 >1) силовые линии увеличивают наклон (см. рисунок) _______________________ * Мы не будем здесь подробно описывать математические преобразования: они просты и практически одинаковы с рассмотренными перед этим. ** Если силовые линии перпендикулярны границе раздела, то их направление не изменяется. |