Давыдков_физика_Ч. 2. Давыдков_физика_Ч. Курс лекций по общей физике предназначен для студентов института дистанционного образования, изучающих вторую часть курса физики
 Скачать 2.62 Mb.
|
1.22. КонденсаторыЕсли взять систему из двух проводников*, имеющих одинаковые по величине и противоположные по знаку заряды, то мы получим конденсатор – устройство, ёмкость которого намного больше ёмкости уединённого проводника и не зависит от ёмкости окружающих тел**. Основной характеристикой конденсатора является его ёмкость С, определяемая выражением  , где q – заряд обкладки конденсатора, 1 – 2 – разность потенциалов между обкладками конденсатора.В данном случае разность потенциалов между обкладками конденсатора равна напряжению на конденсаторе 1 – 2 = U. Поэтому определение ёмкости конденсатора можно записать в таком виде:  .Ёмкость конденсатора зависит от площади обкладок конденсатора, формы обкладок, расстояния между ними, ди-электрической проницаемости вещества, заполняющего прост-ранство между обкладками конденсатора. Рассмотрим в качестве примера плоский конденсатор. Это устройство из двух проводящих плоскостей, параллельных друг другу и разделённых слоем диэлектрика. Если размеры пластин достаточно велики по сравнению с расстоянием d между ними, то заряд распределён по поверхности пластин равномерно с плотностью = q/S. _____________________ * Такие проводники принято называть обкладками. ** Емкость конденсатора не зависит от окружающих тел, поскольку практически все поле сосредоточено между его обкладками. 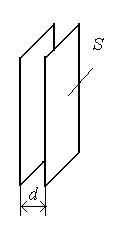 Одна пластина создаёт поле напряжённостью  ; в соответствии с принципом суперпозиции поле между пластинами  , вне пластин Е = 0.Поскольку  , то .Отсюда ёмкость плоского конденсатора  . 1.23. Соединение конденсаторовВ 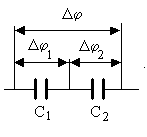 практической деятельности часто используются соединения нескольких конденсаторов. Два основных способа соединения конденсаторов – параллельное и последовательное. Рассмотрим эти способы и рассчитаем суммарную ёмкость всех соединённых конденсаторов.Последовательное соединение. По-следовательным называют соединение конденсаторов, показанное на рисунке. Е С1 С2 сли соединённые таким образом конденсаторы подключить к батарее, то левая обкладка С1 получит от батареи заряд q, а правая обкладка С2 – такой же по величине и противоположный по знаку заряд -q. Внутренние обкладки конденсаторов С1 и С2 заряда от батареи не получают. Но если левая обкладка С1 заряжена положительно, то на правую перетечёт такой же заряд противоположного знака с левой обкладки С2. Поэтому все обкладки конденсаторов будут иметь одинаковые по величине заряды q. При таком соединении суммарная разность потенциалов на всех конденсаторах равна сумме разностей потенциалов на них = 1 + 2. Суммарную разность потенциалов можно выразить через заряд и суммарную ёмкость конденсаторов C:  .Разность потенциалов между обкладками каждого из конденсаторов можно выразить аналогичным образом:  .Заменяя разности потенциалов на приведённые выражения, получаем  и, сокращая заряд, получаем выражение для суммарной ёмкости последовательно соединённых конденсаторов  .Таким образом, величина, обратная суммарной ёмкости конденсаторов, равна сумме обратных каждой из ёмкостей величин. Очевидно, что если соединены не два, а несколько конденсаторов, в сумме будет столько членов, сколько соединено конденсаторов. Параллельное соединение. Параллельным называют показанное на рис 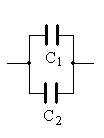 унке соединение конденсаторов.П С1 ри таком соединении разность потен-циалов между обкладками всех конденсаторов одинакова. З С2 аряд на обкладках первого конденсатора q1 = C1, заряд на обкладках второго – q2 = C2. Суммарный заряд на всех конденсаторах q = q1+q2 можно выразить через суммарную ёмкость соединённых конденсаторов: q = C. Это означает, что С = С1 + С2 и суммарная ёмкость конденсаторов, соединённых параллельно, равна сумме ёмкостей всех соединённых конденсаторов: С = С1 + С2. |