Давыдков_физика_Ч. 2. Давыдков_физика_Ч. Курс лекций по общей физике предназначен для студентов института дистанционного образования, изучающих вторую часть курса физики

• Название: Курс лекций по общей физике предназначен для студентов института дистанционного образования, изучающих вторую часть курса физики
• Анкор: Давыдков_физика_Ч. 2.doc
• Дата: 27.02.2018
• Размер: 2.62 Mb.
• Имя файла: Давыдков_физика_Ч. 2.doc
• Тип: Курс лекций; #15985
• страница: 15 из 15

2.1. Электродвижущая сила

Если в проводнике создать электрическое поле, свободные заряды начнут двигаться упорядоченно, т. е. возникнет электрический ток.

Однако этот ток очень быстро прекратится, так как свободные заряды перераспределятся так, что поле внутри проводника станет равно нулю и причина, вызвавшая направленное движение зарядов, исчезнет (см. разд. 1.19).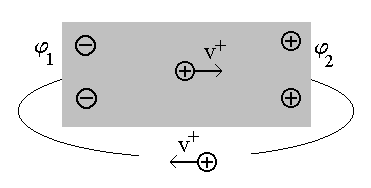



Для того чтобы ток не прекращался, необ-ходимо переносить из-быточные заряды с одного конца провод-ника на противополо-жный. Тогда электри-ческое поле внутри проводника будет су-ществовать непрерывно и направленное движение зарядов не будет прекращаться.

Другими словами – для того чтобы в цепи непрерывно существовал электрический ток, в части электрической цепи свободные носители должны двигаться по электрическому полю, а в другой части – против.

Естественно, электрическое поле не может заставить поло-жительные заряды двигаться против кулоновских сил. Следо-вательно, в части цепи должны действовать силы, заставляющие положительные заряды двигаться от “минуса” к “плюсу”. Такие силы неэлектростатического происхождения принято называть сторонними.

Участок цепи, на котором действуют сторонние силы, называют источником ЭДС (электродвижущей силы).

На практике используются различные виды источников ЭДС. Это электрические генераторы, гальванические элементы (батарейки), аккумуляторы и т. д.

Источник электродвижущей силы характеризуется величиной эдс:

,

где А_ст – работа сторонних сил по перемещению заряда q; q – заряд, перемещённый сторонними силами.

Размерность ЭДС [] = Дж/Кл = В (вольт).

Работу сторонних сил по перемещению заряда q внутри источника эдс можно вычислить следующим образом: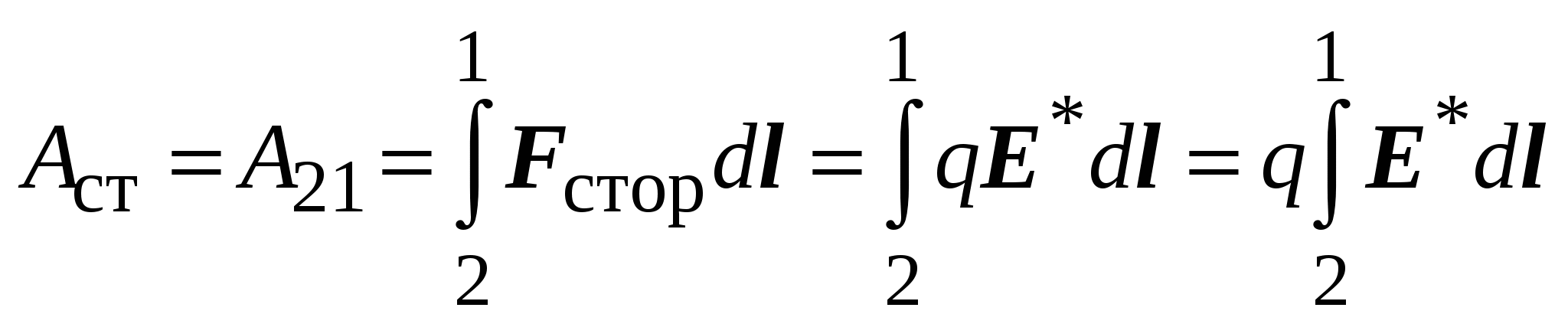

.

Отсюда величина эдс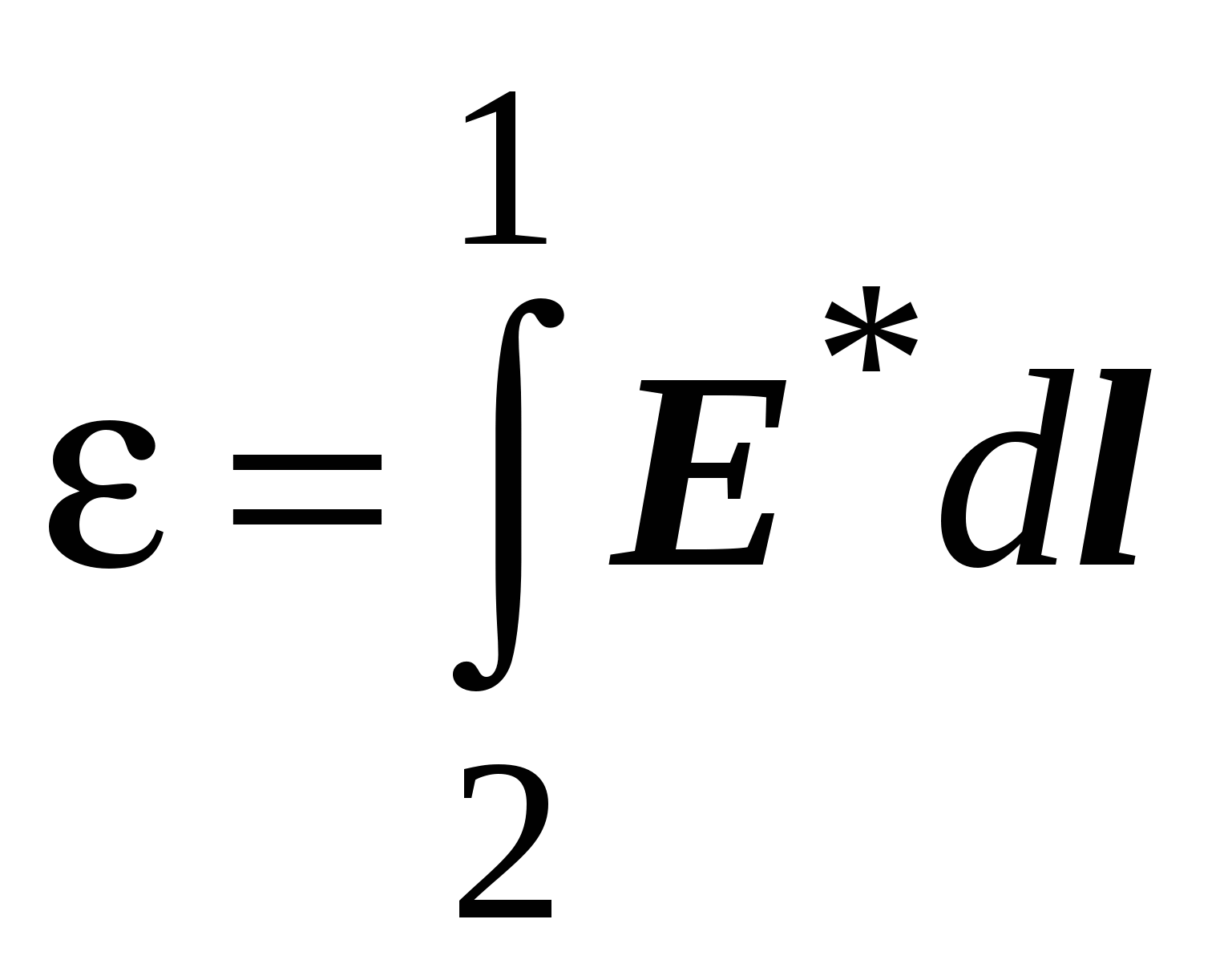

.

Е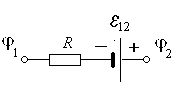сли электрическая цепь замк-нута, то эдс равна

.

Работа по перемещению заряда на участке цепи, содержащем источник ЭДС, может быть найдена как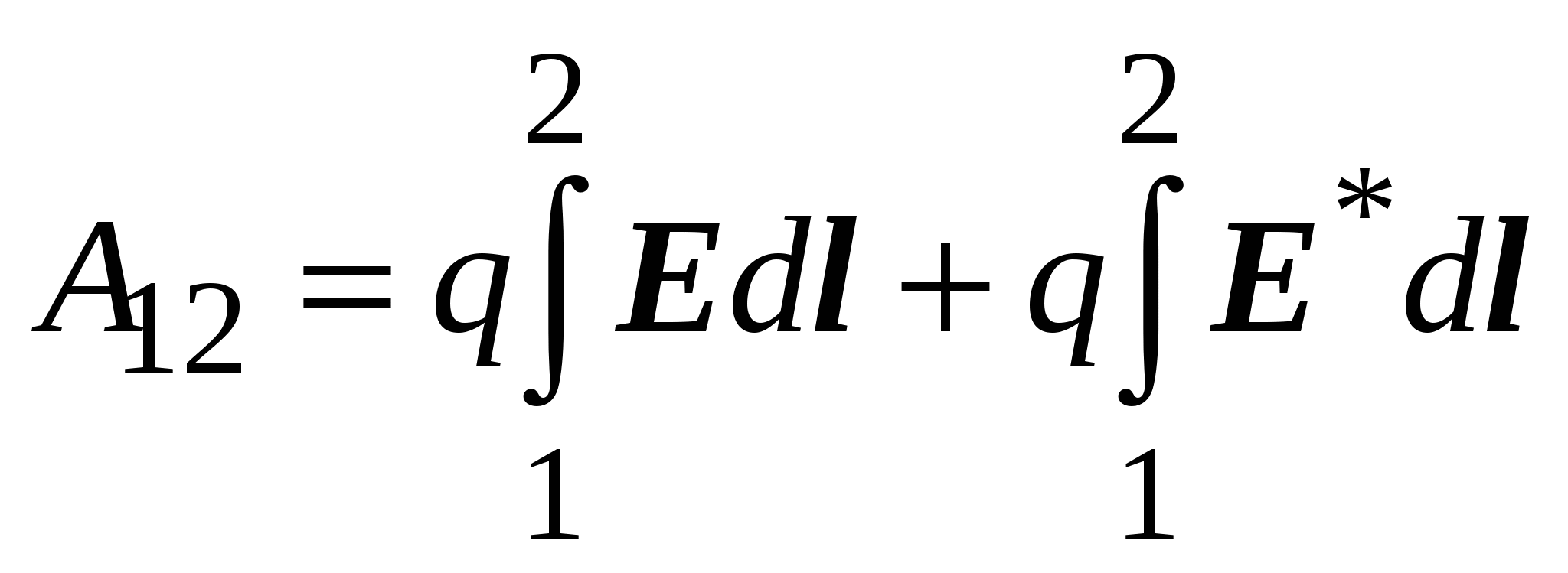

.

Учитывая связь напряжённости и потенциала, а также опреде-ление ЭДС, получаем

.

Величина, равная работе электростатических и сторонних сил по перемещению единичного заряда в электрической цепи, называется напряжением:

.

Обратите внимание: напряжение на участке цепи и разность потенциалов на его концах различны по величине.

Напряжение и разность потенциалов не одно и то же!

Следует отметить, что участок цепи, содержащий источник ЭДС, называют неоднородным. Участок, не содержащий источ-ника ЭДС, называют однородным.

Поскольку однородный участок не содержит ЭДС, постольку , т. е. напряжение на однородном участке цепи равно разности потенциалов на его концах.

2.2. Закон Ома

Георг Ом, экспериментируя с цепями постоянного тока, обнаружил, что сила тока в участке электрической цепи определяется следующим соотношением:

,

где I – сила тока в цепи, U – напряжение на концах цепи, R – сопротивление цепи.

Это выражение принято называть законом Ома для участка цепи.

Сопротивление цепи есть коэффициент, связывающий на-пряжение в цепи и силу тока, возникающего в цепи за счёт напряжения U.

Поскольку размерности силы тока и напряжения не совпадают, R является размерным коэффициентом. Размерность сопротивления можно получить из закона Ома: [R] = [U]/[I] =
= В/А = Ом.

Величина сопротивления цепи при постоянной температуре зависит от размеров и формы проводников цепи, от материала, из которого проводники изготовлены. Увеличение температуры у большинства проводников вызывает возрастание сопротивления.

Для однородного по составу проводника постоянной длины и сечения сопротивление , где  – удельное сопротивление
проводника*; l – длина проводника, S – площадь поперечного сечения проводника.

Закон Ома для участка цепи может быть записан в диф-ференциальной форме

,

где j – плотность тока в проводнике;  – удельное сопротивление проводника;  – удельная электрическая проводимость провод-ника; Е – напряжённость электрического поля в проводнике.

Если участок цепи неоднороден, то кроме электростатических сил на свободные заряды действуют и сторонние, тогда

J = E + E^*.

Это выражение представляет собой закон Ома в диф-ференциальной форме для неоднородного участка цепи.

В интегральной форме это выглядит так: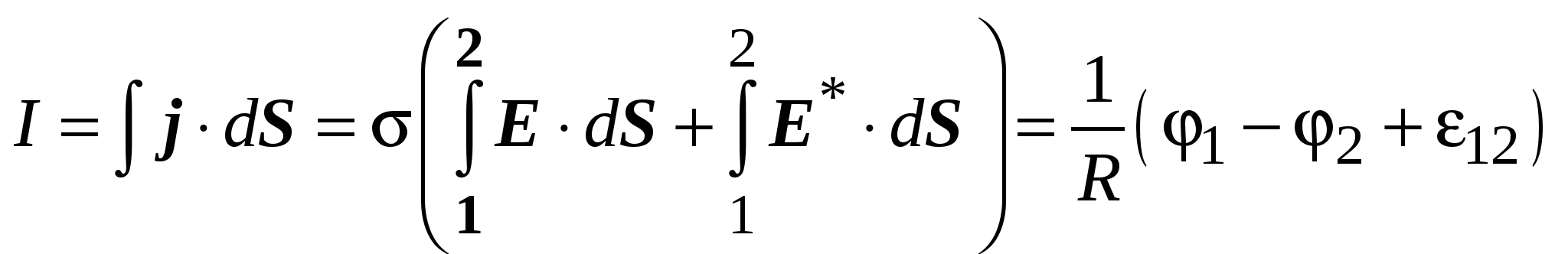



и



где _{1 –} ₂ – разность потенциалов на концах участка цепи.

Последнее выражение представляет собой закон Ома для неоднородного участка цепи в интегральной форме.

Если неоднородная цепь замкнута, то ₁ = ₂ (так как концы участка цепи соединены между собой) и закон Ома принимает следующий вид:

,

где R – суммарное сопротивление однородного участка цепи и внутреннего сопротивления источника ЭДС.

Это выражение представляет собой закон Ома для замкнутой цепи.

___________________________
* Удельное сопротивление зависит от материала проводника; размерность удельного сопротивления – Омм.

2.3. Работа и мощность тока. Закон Джоуля-Ленца

Рассмотрим участок цепи, напряжение на концах которой равно U.

В рассматриваемой цепи будет протекать электрический ток, сила которого, в соответствии с законом Ома, равна U/R.

По определению (см. разд. 2.1), напряжение равно работе электростатических и сторонних сил по перемещению единичного заряда в электрической цепи. Следовательно, при протекании тока кулоновские и сторонние силы, действующие на заряды в рассматриваемом участке, совершат работу

.

Эту работу называют работой электрического тока.

Если ток постоянный, то q = It, где I – сила тока, t – время, в течение которого в проводнике течёт ток. В этом случае работа тока может быть рассчитана по формуле

.

Поскольку , постольку работа тока

.

Таким образом, работа тока может быть рассчитана с помощью нескольких формул. Какое именно выражение следует использовать в конкретной задаче, определяется её условием. Например, если в условии дана сила тока и разность потенциалов на концах однородного участка цепи, то , если же известны сила тока и сопротивление цепи, то .

Мощность есть работа, совершённая за единицу времени: . Поэтому мощность тока можно рассчитать по следующим формулам:

.

Если проводник с током неподвижен и ток не вызывает химических реакций, то вся работа идёт на увеличение внут-ренней энергии проводника, т. е. на его нагрев.

Другими словами – при протекании тока в проводнике выделяется тепло

.

В 1841 г. англичанин Джеймс П. Джоуль и независимо от него в 1842 г. русский физик Эмилий Христианович Ленц, обобщая результаты своих экспериментов, получили именно такое выражение для расчета количества тепла, выделяемого про-водником при протекании в нём тока. Поэтому последнее выражение принято называть законом Джоуля–Ленца.

Если сила тока изменяется с течением времени, то количество тепла, выделяющееся в цепи, можно рассчитать с помощью следующих выражений: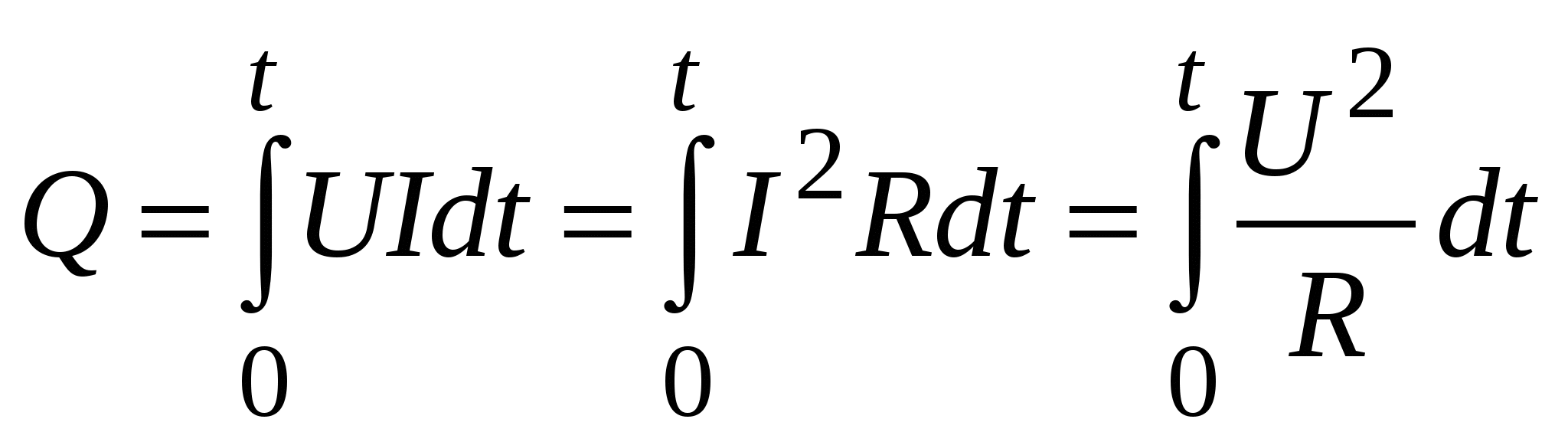

.
Закон Джоуля–Ленца может быть записан и в дифференциальной форме:

,

где  – удельная тепловая мощность тока (это количество тепла, выделяющееся за единицу времени в единице объёма проводника).

3. Магнитное поле в вакууме

3.1. Магнитное поле. Источник магнитного поля. Характеристики магнитного поля

В начале XIX в. физики полагали, что магнитное поле создаётся постоянными магнитами природного происхождения. Но было также известно, что иногда после удара молнии металлические предметы намагничивались. Это наводило на мысль о том, что магнетизм и электрический ток (молния) каким-то образом связаны между собой.

Зимой 1819 г. Ганс Христиан Эрстед заметил, что магнитная стрелка, висящая параллельно проводнику, отклоняется при включении тока.

При изменении направления тока на противоположное стрелка отклонялась в противоположном направлении.

Так было обнаружено, что магнитное поле создаётся элект-рическим током.

Другими словами – магнитное поле создаётся зарядами, которые упорядоченно движутся относительно наблюдателя.

Обратите внимание на важную деталь: для наблюдателя, относительно которого заряженные частицы движутся упоря-доченно, существует магнитное поле, созданное этими зарядами.

Но для наблюдателя, который движется вместе с этими же заряженными частицами, магнитного поля нет! Для этого наблюдателя существует только электростатическое поле, созданное неподвижными относительно него зарядами.

Это означает, что возникновение магнитного поля является проявлением релятивистских эффектов.

Изменение направления тока в опыте Эрстеда вызвало изменение направления отклонения магнитной стрелки. Следовательно, магнитное поле имеет направленный характер. Отсюда вывод – магнитное поле должно характеризоваться векторной величиной.

Основной силовой характеристикой магнитного поля является индукция магнитного поля. Эту характеристику принято обозначать символом В. Размерность индукции [B] = Тл (тесла).

Кроме индукции В используется вспомогательная харак-теристика магнитного поля Н, которую принято называть напряжённостью магнитного поля. Размерность напряжённости
[Н] = А/м.

3.2. Индукция магнитного поля, созданного движущимся точечным зарядом

Рассмотрим заряд q, движущийся с постоянной скоростью v.

Заряд движется, следовательно он создаёт магнитное поле.

Экспериментально установлено, что индукция B магнитного поля, созданного этим зарядом в интересующей нас точке, равна

,

где r – радиус-вектор, начинающийся на заряженной частице и заканчивающийся в интересующей нас точке; r – модуль вектора r ; _о – магнитная постоянная; . _о = 4^.10^-7Гн/м.

Как следует из последнего выражения, вектор В перпендику-лярен плоскости, в которой лежат векторы v и r. На приведён-ном рисунке вектор В в соответствии с правилом правого винта, направлен на нас (векторы v и r лежат в плоскости рисунка).

В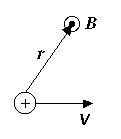ыражение для расчёта В позволяет выявить ряд существенных факторов, влияю-щих на величину индукции магнитного поля.

Во-первых, магнитное поле создаётся дви-жущимися зарядами. Следовательно, магнит-ная индукция должна зависеть от величины заряда q. Эксперимент подтвердил, что ин-дукция В прямо пропорциональна q.

Во-вторых, магнитное поле, создаётся движущимися зарядами. Причём вследствие релятивистского характера оно должно быть тем сильнее, чем больше скорость заряда. И действительно, В прямо пропорциональна скорости заряда v.

В-третьих, магнитное поле должно ослабевать по мере удаления от движущегося заряда. Из выражения для расчёта В следует, что индукция магнитного поля, созданного движущимся зарядом, действительно обратно пропорциональна квадрату модуля радиус-вектора r, определяющего положение точки в пространстве относительно заряда.

Если необходимо рассчитать магнитное поле, созданное несколькими движущимися зарядами, следует использовать принцип суперпозиции .

3. Закон Био–Савара–Лапласа

Найдём выражение для расчёта индукции магнитного поля, созданного током I.

В элементарном участке проводника dl содержится n^.dl^.S свободных носителей заряда, где n – концентрация свободных носителей заряда, dl – длина элементарного участка проводника, S – площадь поперечного сечения проводника.

Каждый из зарядов создаёт в интересующей нас точке магнитное поле, индукция которого

,