Давыдков_физика_Ч. 2. Давыдков_физика_Ч. Курс лекций по общей физике предназначен для студентов института дистанционного образования, изучающих вторую часть курса физики

• Название: Курс лекций по общей физике предназначен для студентов института дистанционного образования, изучающих вторую часть курса физики
• Анкор: Давыдков_физика_Ч. 2.doc
• Дата: 27.02.2018
• Размер: 2.62 Mb.
• Имя файла: Давыдков_физика_Ч. 2.doc
• Тип: Курс лекций; #15985
• страница: 14 из 15

1.24. Энергия заряженных проводников

Для того чтобы сообщить любому заряженному проводнику дополнительный заряд, необходимо совершить работу



(здесь предполагается, что потенциал бесконечно удалённой точки равен нулю).

Работа, необходимая для того, чтобы зарядить проводник от нулевого потенциала до потенциала 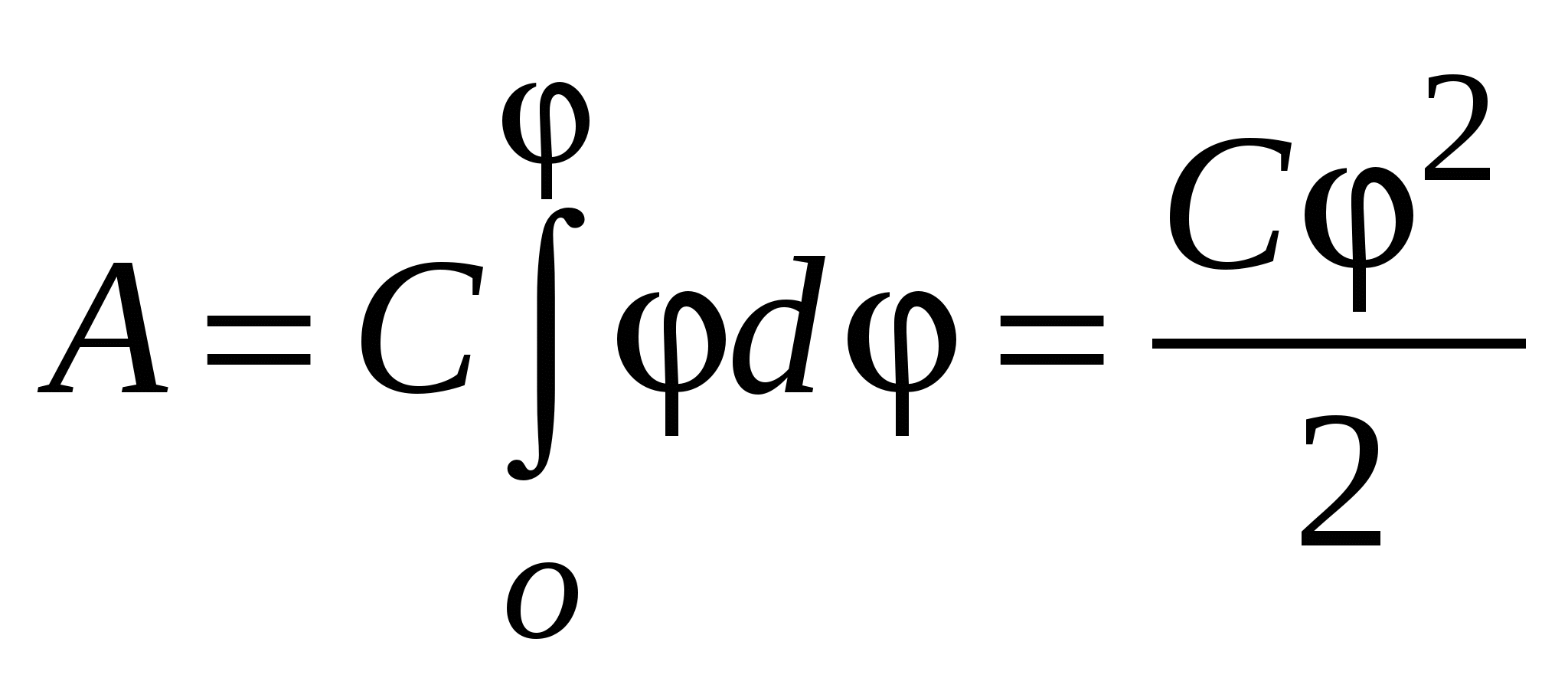

.

Поскольку эта работа идёт на увеличение энергии заряжен-ного проводника, его энергия равна

.

Для конденсатора элементарная работа

,

работа, необходимая для заряда конденсатора от нулевого потенциала до потенциала ,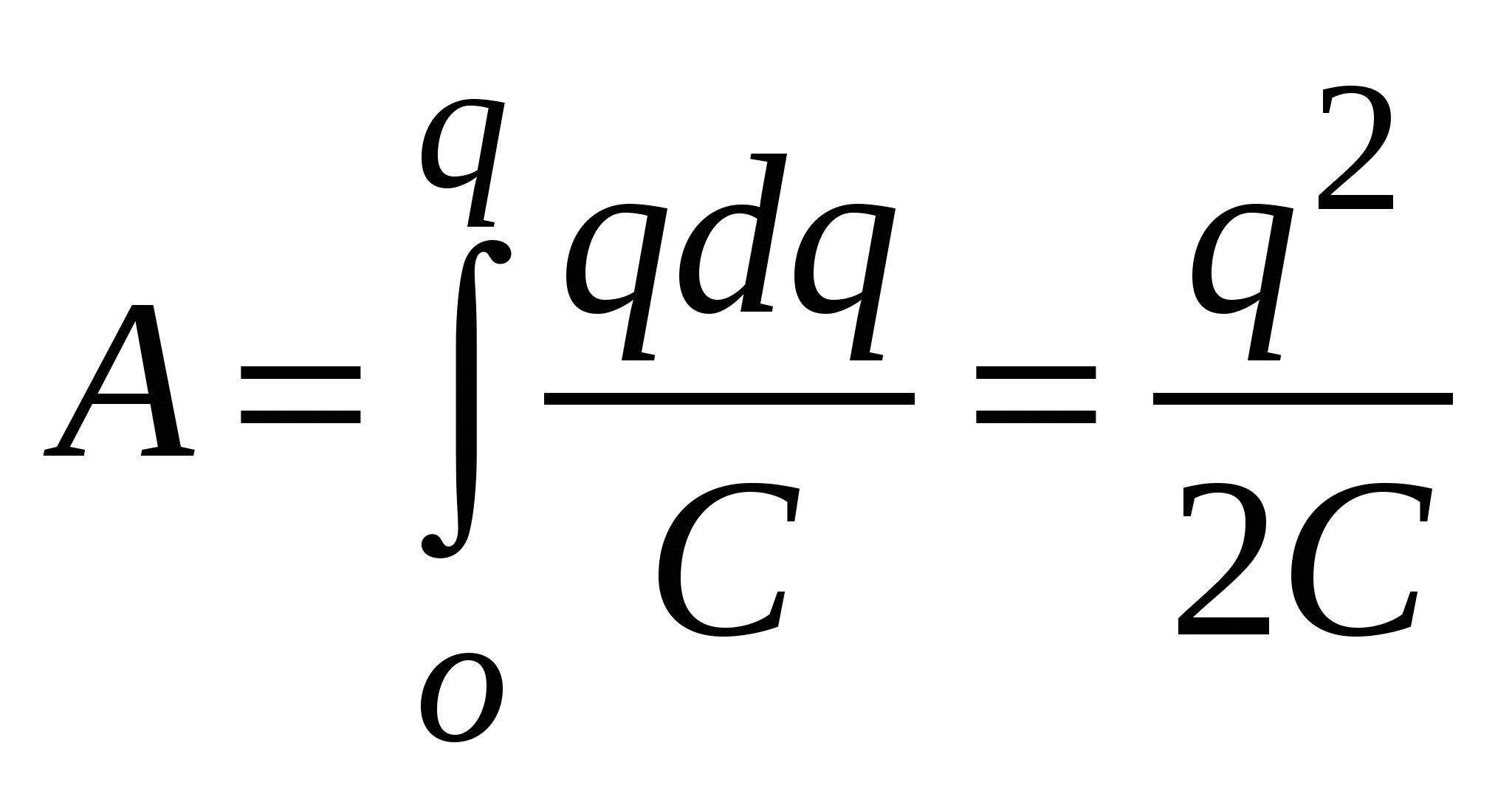

;

а энергия конденсатора

.

Последнюю формулу можно переписать в виде



(так как заряд второй пластины q₂ = -q₁).

Подобное выражение применимо и к системе из n заряженных проводников. Энергия такой системы

.

1.25. Энергия электрического поля

Вернёмся к выражению электрической энергии, запасённой в конденсаторе:

.

Для плоского конденсатора . Поэтому его энергия



и

.

В последние два выражения для расчёта энергии не входят характеристики проводников (S и d); в них энергия выражается через характеристики электрического поля. Это позволяет трактовать W как энергию электрического поля. Мы можем говорить, что это энергия электрического поля. И эта энергия распределена в пространстве с объёмной плотностью

.

Используя последнее выражение, можно найти энергию, запасённую в однородном электрическом поле, занимающем объём V

W = V.

Если электрическое поле неоднородно, то

,

т. е. энергия поля в объёме V равна интегралу от объёмной плотности электрического поля, взятому по объёму V.

1. . Постоянный электрический ток

Электрический ток – это упорядоченное движение электрических зарядов.

Для того чтобы свободные заряды двигались в среде упорядоченно, необходимо либо наличие электрического поля, либо какое-либо поле неэлектростатических сил.

Если свободные заряды движутся упорядоченно в электри-ческом поле, то причиной, вызывающей электрический ток, являются кулоновские силы.

Если же свободные заряды движутся упорядоченно без электрического поля, то причиной, вызывающей электрический ток, являются силы, называемые сторонними (например, магнитные силы в генераторе электрического тока). Причём, если электрическое поле характеризуют напряжённостью Е, то поле сторонних сил – так называемой напряженностью поля сторонних сил Е^*.

Количественной характеристикой электрического тока является сила тока I. Это величина, равная отношению заряда dq, переносимого через поверхность за время dt, ко времени dt

.

Сила тока, как это видно из определения, – скалярная величина.

В системе СИ единицей измерения силы тока является ампер [I] = Кл/с = А.

Электрический ток может быть обусловлен направленным движением как положительных, так и отрицательных зарядов. Причём, если ток создаётся одновременным движением положи-тельных зарядов dq⁺ (они движутся по полю) и отрицательных зарядов dq^- (они движутся против электрического поля), то

.

Электрический ток имеет направление. Это – условная характеристика.

Направлением тока принято считать направление движения положительных зарядов (если ток создают отрицательные заряды, то направление тока противо-положно направлению их движения).

В общем случае величина отношения dq/dt может меняться со временем; если же dq/dt =constто ток называют постоянным и тогда можно считать I = q /t.

Величина отношения dq / dt может зависеть не только от времени, но и от координаты: в разных точках сечения провод-ника оно может быть разным. Поэтому для характеристики электрического тока используют дифференциальную характе-ристику, именуемую плотность тока j:

,

где n – единичный вектор, параллельный скорости направленного движения положительных зарядов; dS_ – площадь элементарной поверхности, перпендикулярной скорости направленного движе-ния зарядов.

Размерность плотности тока [j] = A/м².

Сила тока и плотность тока связаны между собой:

.

Последнее выражение можно прочесть и так: сила тока через поверхность S равна потоку вектора плотности тока j через эту поверхность.



Протекание электрического тока не вызывает накопления заряда в проводнике. Это означает, что если в некоторый объём проводника вошёл заряд dq, то такой же заряд должен выйти из этого объёма.

В математической форме послед-нее утверждение имеет следующий вид:

.

Найдём связь плотности тока со средней скоростью упорядоченного движения зарядов в проводнике. Для этого выберем единичную поверхность, перпендикулярную скорости упорядоченного движения зарядов. За единицу времени через неё пройдёт n⁺vположительных зарядов и n  v отри-цательных зарядов (здесь n⁺, n^- – концентрации положительных и отрицательных зарядов соответственно, v⁺, v^- – скорости направленного движения зарядов). Тогда плотность тока

j = e⁺  n⁺  v⁺ + e^-  n^-  v ^- .

В отсутствие электрического поля свободные носители заряда движутся хаотически. Это движение не даёт вклада в j, так как средняя скорость хаотического движения равна нулю.