Давыдков_физика_Ч. 2. Давыдков_физика_Ч. Курс лекций по общей физике предназначен для студентов института дистанционного образования, изучающих вторую часть курса физики
 Скачать 2.62 Mb.
|
1.8. Работа электростатических силЕсли заряд движется в электростатическом поле, то кулоновская сила совершает работу. Найдём величину работы, совершаемой при перемещении заряда в электростатическом поле. Д 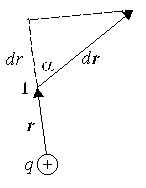 опустим, что заряд qо перемещается на dr из точки 1 в электрическом поле точечного заряда q.При этом совершается элементарная работа, равная А = Fdr. Учитывая, что кулоновская сила  , получаем А =  .Из рисунка видно, что rdr = rdr. Поэтому  .На конечном перемещении из точки 1 в точку 2 работа электростатических сил 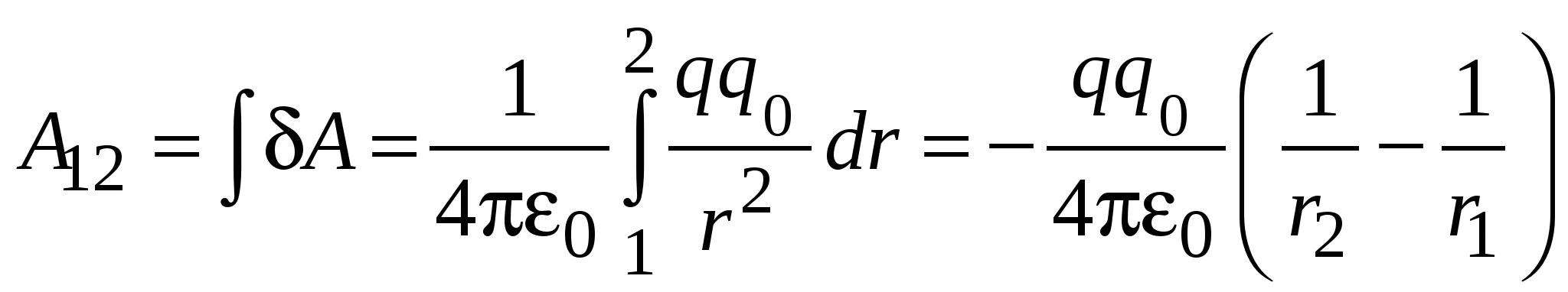 .Таким образом, работа по перемещению заряда в электростатическом поле зависит от величины заряда (зарядов), создающего поле, величины перемещаемого заряда и его начального и конечного положений. Обратите внимание на то, что в выражении для расчёта работы отсутствует информация о промежуточных положениях заряда qо. Следовательно, работа в электростатическом поле не зависит от формы траектории. В соответствии с данным в механике определением, такое поле является консервативным, т. е. электростатическое поле консервативно. Как известно, в консервативном поле работа совершается за счёт убыли потенциальной энергии и не зависит от формы траектории A = U1 – U2= -U, где U1 и U2 – потенциальная энергия заряда в начальной и конечной точках траектории соответственно; U – приращение потенциальной энергии. Следовательно, работа кулоновских сил при перемещении заряда в электростатическом поле равна убыли потенциальной энергии перемещаемого заряда, не зависит от формы траектории, по которой перемещался заряд, а зависит лишь от начального и конечного положений заряда. Как уже отмечалось выше, работа, производимая силами поля, совершается за счёт убыли потенциальной энергии переме-щаемого заряда, т. е.  .Последнее выражение позволяет найти выражение для расчёта потенциальной энергии заряда в электростатическом поле. 1.9. Циркуляция вектора напряжённостиЕсли начальная и конечная точки траектории заряда совпа-дают, то его потенциальная энергия в начальной и конечной точках траектории одинакова. Следовательно, и работа по пере-мещению заряда по замкнутому контуру будет равна нулю  .Сила, действующая на заряд в электрическом поле напряжённостью Е, равна F = qE. Это означает, что  .Поскольку q = const, заряд можно вынести за знак интеграла. Значение заряда отлично от нуля, поэтому нулю должен равняться интеграл  .В математике интеграл по замкнутому контуру от скалярного произведения вектора на бесконечно малый элемент этого контура принято называть циркуляцией. Следовательно, циркуляция вектора Е в электрическом поле, созданном неподвижными зарядами, всегда равна нулю  ;(здесь вместо dr используется обозначение dl, так как математики при расчёте циркуляции традиционно используют это обозначение). 1.10. Потенциал электростатического поляИз сравнения выражений A12 = -(U2 – U1) и  , полученных в разд.1.8, видно, что потенциальная энергия заряда qo, находящегося в поле, созданном точечным зарядом q, равна  ,где r – расстояние между зарядами. Важно напомнить, что значение потенциальной энергии зависит от выбора точки отсчёта. В электростатике в качестве точки отсчёта выбирают бесконечно удалённую точку. Потен-циальная энергия заряда в такой точке считается равной нулю. В то же время разность потенциальных энергий не зависит от выбора точки отсчёта и имеет абсолютное значение. Из последнего выражения видно, что потенциальная энергия заряда в электростатическом поле зависит от величины зарядов и расстояния между ними. Но если мы разделим потенциальную энергию пробного заряда q0 на его величину, то результат будет зависеть лишь от величины заряда, создающего поле, и рас-стояния r  .Следовательно, величина отношения U/q0 является характе-ристикой электростатического поля. Эту характеристику называют потенциалом электростатического поля и обозначают  ,где U – потенциальная энергия заряда q0, находящегося в электростатическом поле, созданном другим зарядом (или зарядами). Потенциал является скалярной величиной. Размерность потенциала [] = В = Дж/Кл (вольт). Потенциал является энергетической характеристикой электро-статического поля, поскольку определяет энергию заряда q, обусловленную его взаимодействием с электрическим полем: U = = q (обратите внимание: здесь q – величина заряда, помещён-ного в электрическое поле, созданное другим зарядом или зарядами). Используя потенциал, можно найти работу по перемещению заряда q из одной точки в другую как A12 = -q(2-1). Возвращаясь к полученному ранее выражению для расчёта потенциальной энергии взаимодействия двух точечных зарядов, мы можем записать выражение для расчёта потенциала точки в поле, созданном точечным зарядом q  .Значение потенциала в данной точке как и значение потенциальной энергии зависит от выбора точки отсчёта. Обычно полагают, что нулю равен потенциал точки, находящейся бесконечно далеко от заряда, создающего поле. Разность потенциалов, как и разность значений потен-циальных энергий, от выбора точки отсчёта не зависит, а полностью определяется взаимным расположением интере-сующих нас точек в электрическом поле. |