Давыдков_физика_Ч. 2. Давыдков_физика_Ч. Курс лекций по общей физике предназначен для студентов института дистанционного образования, изучающих вторую часть курса физики

• Название: Курс лекций по общей физике предназначен для студентов института дистанционного образования, изучающих вторую часть курса физики
• Анкор: Давыдков_физика_Ч. 2.doc
• Дата: 27.02.2018
• Размер: 2.62 Mb.
• Имя файла: Давыдков_физика_Ч. 2.doc
• Тип: Курс лекций; #15985
• страница: 5 из 15

1.7. Примеры расчёта напряжённости полей

с помощью теоремы Гаусса

Рассмотрим несколько примеров расчёта электростатических полей с помощью теоремы Гаусса.

1.7.1. Поле бесконечной равномерно заряженной

прямолинейной нити

Рассмотрим равномерно заряженную бесконечно длинную нить. Линейная плотность заряда равна .

Заряд, равномерно распределённый по нити, обладает симметрией – он симметричен относительно оси.

Н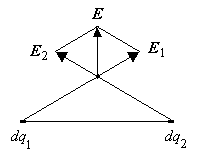ить имеет бесконечную длину, поэтому любому эле-ментарному заряду dq₁ можно сопоставить другой элементарный заряд dq₂, расположенный симметрично относительно некоторой точки в электростатическом поле.

Поскольку расстояние от эле-ментарных зарядов до этой точки одинаково, модули напряжён-ностей Е₁ и Е₂ одинаковы. Поэтому результирующая напряжённость

Е = Е₁+Е₂ направлена перпен-дикулярно нити (см. рисунок).

Очевидно, что и в других точ-ках, расположенных на таком же расстоянии от нити, напря-жённость будет иметь такую же величину и направление.

Элементарные заряды и точка в поле были выбраны случайно, поэтому вывод справедлив как для всех остальных элементарных зарядов, так и для всех точек поля.

Это означает, что электрическое поле, созданное заряженной нитью, симметрично относительно оси нити. Другими словами – симметрия поля тождественна симметрии заряда, создающего поле.

Таким образом, векторы напряжённости во всех точках окружающего пространства перпендикулярны нити и модули напряжённости на одинаковых расстояниях от нити одинаковы.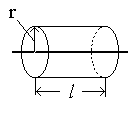



Расчёт напряжённости поля с помощью теоремы Гаусса следует начинать с получения выражения для потока вектора Е.

В свою очередь, выражение для потока следует начинать с выбора формы замкнутой поверхности и её положения относительно источника поля.

Расчёт потока будет максимально прост, если выбрать такую поверхность, симметрия которой идентична симметрии создаю-щего поле заряда.

В данном случае удобно пользоваться замкнутой поверхностью с осевой симметрией.

Такой поверхностью является цилиндр, ось которого совпадает с нитью. Пусть высота цилиндра равна l, а радиус основания – r.

Поток вектора напряжённости поля, созданного нитью, складывается из потока через торцевые поверхности цилиндра и потока через боковую поверхность.

Поток через торцевые поверхности равен нулю, так как векторы напряжённости перпендикулярны нити и, соответ-ственно угол между векторами Е и n равен 90^0,

.
Поток через боковую поверхность

.

Поскольку все точки боковой поверхности расположены на одинаковых расстояниях от нити, модули напряжённости во всех точках боковой поверхности цилиндра одинаковы, т. е.

.

Таков вид выражения для потока вектора рассчитываемой напряжённости.

Следующий этап вычисления напряжённости электро-статического поля – расчёт суммарного заряда, охваченного замкнутой поверхностью.

Заряд, охваченный поверхностью s, можно найти так:

.

Тогда, по теореме Гаусса,



или

.

Отсюда

.

Таким образом, напряжённость электрического поля, создан-ного равномерно заряженной нитью, прямо пропорциональна линейной плотности заряда нити и обратно пропорциональна расстоянию от нити до интересующей нас точки.

Обратите внимание – напряжённость обратно пропорцио-нальна первой степени расстояния от нити (напряжённость поля точечного заряда обратно пропорциональна квадрату расстояния от заряда).

1.7.2. Поле бесконечной равномерно заряженной плоскости

Пусть имеется бесконечная равномерно заряженная плоскость. Поверхностная плотность заряда равна .

Из симметрии системы следует, что поле должно быть симметричным относительно плоскости (это можно доказать примерно так же, как в предыдущем примере). Следовательно, вектор Е везде перпендикулярен плоскости и в одинаково удалённых от плоскости точках модули вектора Е одинаковы.

В этом случае в качестве поверхности интегрирования целесообразно выбрать цилиндр, ориентированный так, как показано на рисунке.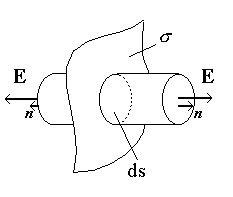



Поток вектора Е и здесь складывается из потока через боковую поверхность цилиндра и потока через торцы цилиндра: Ф = Ф_бок + 2Ф_торц.

Поток вектора напряжённости через боковую поверхность равен нулю, так как в силу симметрии поля вектор напряжённости дол-жен быть параллелен боковой поверхности и

.

Поток вектора напряжённости через торцевые поверхности , где r – радиус основания цилиндра.

Полный поток через оба торца цилиндра Ф = 2Еr².

Суммарный заряд, охваченный поверхностью цилиндра, равен .

Отсюда и .

Полученное выражение показывает, что напряжённость поля, созданного бесконечной равномерно заряженной плоскостью, прямо пропорциональна поверхностной плотности заряда и не зависит от расстояния.

Обратите внимание: в этом случае напряжённость элект-рического поля на любых расстояниях от плоскости одинакова!

1.7.3. Поле двух параллельных равномерно заряженных плоскостей с одинаковым по величине и противоположным по знаку зарядом

Пусть имеются две параллельные плоскости, заряды которых одинаковы по величине и противоположны по знаку. Поверх-ностные плоскости зарядов соответственно равны  и -.

Напряжённость поля, созданного двумя плоскостями, в соответствии с принципом суперпозиции может быть найдена как векторная сумма напряжённостей, созданных каждой плоскостью в отдельности, Е = Е₁ + Е₂.

Н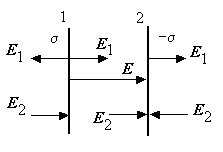апряжённости полей, созданных каждой из плоскостей, во всех точках пространства одинаковы по величине и противоположны по направ-лению (так как заряды плоскостей одинаковы по величине и противопо-ложны по знаку).

Это означает, что напря-жённость поля между плас-тинами равна удвоенной напряжённости поля, созданного одной пласти-ной, .

Напряжённость поля вне пластин равна нулю.

1.7.4. Поле равномерно заряженной сферы

Пусть имеется сфера радиуса r_о, по которой равномерно распределён заряд q.

Из симметрии системы следует, что поле должно быть сим-метрично относительно центра заряженной сферы. Следова-тельно, вектор Е во всех точках пространства направлен параллельно радиальным прямым и на равных расстояниях от центра сферы модули Е одинаковы.

В этом случае в качестве поверхности интегрирования целесообразно выбрать сферическую поверхность, центр которой совпадает с центром заряженной сферы.

Пусть радиус сферической поверхности меньше, чем радиус заряженной сферы. В этом случае суммарный заряд, охваченный поверхностью, равен нулю (так как внутри сферы зарядов нет, все заряды расположены на её поверхности).

Это означает, что внутри заряженной сферы поток вектора напряжённости через поверхность, радиус которой r_o>r>0, равен нулю.

Площадь поверхности отлична от нуля, поэтому поток может быть равен нулю лишь в том случае, если напряжённость поля внутри сферы равна нулю.

Следовательно, напряжённость электрического поля внутри заряженной сферы равна нулю Е(r_o  r > 0) = 0.

Пусть радиус поверхности интегрирования больше радиуса заряженной сферы. В этом случае суммарный заряд, охваченный поверхностью, равен заряду сферы q.

Если единичный вектор n направлен наружу от поверхности, то угол между n и Е во всех точках равен нулю (или 180^о, если заряд сферы отрицательный).

Отсюда следует, что .

Поскольку модуль вектора Е во всех точках выбранной поверхности одина-ков и площадь сферы равна , по-стольку поток вектора напряжённости электрического поля

.

В соответствием с теоремой Гаусса поток вектора Е пропорционален сумме зарядов, охваченных поверхностью:

.

Следовательно, напряжённость электрического поля, создан-ного заряженной сферой снаружи от неё, равна

.

Обратите внимание на то, что поле вне заряженной сферы совпадает с полем точечного заряда q (см. разд. 1.3).