Росноу Ильина Г.Г.Статистика Лекции. Курс лекций по статистике автор ильина г. Г.,к э. н., проф кафедры Финансы и банковское дело,росноу. Тема Общее понятие о статистике. План Общее понятие о статистике и о ее предмете. Основные категории статистики
 Скачать 0.63 Mb. Скачать 0.63 Mb.
|
|
Тема5. Средние величины и показатели вариации. План. 1.Средние величины , их виды и характеристика. 2. Средняя арифметическая величина простая и взвешенная. 3.Структурные средние : Мода, Медиана. Соотношение моды , медианы и средней величины. 4. Степенные средние и порядок их расчета. 5.Показатели вариации и их виды. 6. Среднеквадратическое отклонение и дисперсия, их характеристики. 7. Коэффициент вариации- относителый показатель вариации. 8. Свойство об общих и частных средних и дисперсий. Средние величины широко применяются в экономическом анализе. Средние величины являются обобщающими характеристиками качественно-однородной совокупности, именованной величиной, а также абстрактной величиной средней величины, как правило, не равны ни одному из вариантов. Существуют различные виды средних величин: средняя арифметическая простая и взвешенная, средняя гармоническая, средняя геометрическая, средняя хронологическая и др. Самой распространенной средней является средняя арифметическая. Простая средняя арифметическая величина применяется тогда, когда каждая единица статистической совокупности встречается один раз или одинаковое число раз. Она равна: 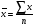 , где , гдех – единицы (вариант) статистической совокупности, n – объем совокупности. Средняя взвешенная арифметическая тогда, когда каждый вариант встречается неодинаковое число раз, в совокупности равна: 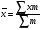 , где , гдеm– частота, которая показывает, сколько раз каждый вариант встречается в совокупности. Например, при сдаче экзамена 24 студента получили следующие оценки: пять студентов пятерки, десять студентов четверки, шесть студентов тройки и три студента двойки. Надо найти средний балл студентов на экзамене. Средний балл в группе равен: 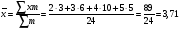 балла балла
К структурным средним величинам относятся величины,которые показывают структуру распределения единиц статистической совокупности.К ним относятся мода, медиана.Мода- вариант,который чаще всего встречается в совокупности,а медиана- вариант , который делит распределение пополам. Кроме моды и медианы для характеристики структуры распределения значений признака изучаются квартили: нижняя и верхняя. Квартиль нижняя - 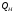 (значение признака, который делит ряд распределения в отношении 1/4 к 3/4 всех ответов), квартиль верхняя - (значение признака, который делит ряд распределения в отношении 1/4 к 3/4 всех ответов), квартиль верхняя -  (квартиль верхняя, который делит ряд распределения в отношении 3/4 к 1/4 всех ответов). (квартиль верхняя, который делит ряд распределения в отношении 3/4 к 1/4 всех ответов).Показывает ассиметрия распределение признака соотношение Мо,Ме и средней величины; а также соотношение полусуммы квартилей и медианы. 4.Степенные средние. Средняя гармоническая величина применяется тогда, когда нет достаточно исходных данных для её расчета. Она равна:  , где , где - произведение вариантов на соответствующие частоты. - произведение вариантов на соответствующие частоты.Как показано выше средняя арифметическая взвешенная применяется тогда, когда известны варианты х и их частоты m. А средняя гармоническая взвешенная применяется тогда, когда отсутствует данные по частотам m, а представлено произведение вариантов на частоты 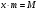 . .Рассмотрим среднюю цену яблок по трем магазинам по следующим данным. Таблица 2 Цена и выручка от реализации яблок по 3-м магазинам
Средняя цена 1 кг яблок = 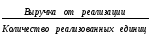 Определяющим показателем в данном примере является числитель этой «неявной формы средней», т.е. известна выручка от реализации М (числитель), а количество реализованных единиц неизвестно, но может быть найдена как частное от деления выручки от реализации (М) на цену яблок (х) по каждому магазину. Таким образом, средняя цена яблок определяется по средней гармоничной и равна: 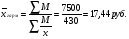 В статистике существует негласные правила определения формулы средней: Правило 1. Если по неявной форме средней дан знаменатель, то средняя определяется по формуле средней арифметической. Правило 2. Если по неявной форме средней дан числитель, то средняя определяется по формуле средней гармонической.
Для полной характеристики статистической совокупности необходимо рассчитать среднеквадратическое отклонение, которое изучает вариацию внутри совокупности. Оно равно: 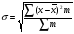 Изучить степень вариации позволят коэффициент вариации – относительный показатель вариации, который равен: 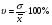 Если коэффициент вариации менее 40%, то колебание внутри рассматриваемой совокупности незначительная и совокупность качественно однородна. Если коэффициент вариации более 40%, то колеблемость внутри совокупности значительная и совокупность неоднородна. Тема 6. РЯДЫ ДИНАМИКИ. ПЛАН.
6.1. скользящей средней; 6.2 аналитического выравнивания. 7. Индексы сезонности. 8. Прогнозирование ряда динамики методом: 8.1.точечных оценок; 8.2. интервальных оценок. 1.Ряд динамики — это последовательность упорядоченных во времени количественных статистических величин, характеризующих развитие изучаемого явления или процесса. Конкретное значение величины называется уровнем ряда и обозначается Y, а их число в ряду обозначается n. Ряды динамики классифицируются по по времени — моментные и интервальные, которые показывают уровень явления на конкретный момент времени или за определенный его период. По интервалам времени — ряды динамики бывают с равноотстоящими и неравноотстоящими интервалами времени. 2.Средние уровни в рядах динамики. В зависимости от вида ряда динамики алгоритмы средних величин рассчитываются по разным формулам. В интервальных рядах динамики средняя рассчитывается по простой арифметической величине. В моментных рядах динамики с равноотстоящими уровнями применяется : Средняя хронологическая величина применяется в моментных рядах динамики с равноотстоящими уровнями. Она равна: 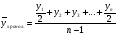 , где , где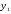 и и  – уровни первого и последнего года – уровни первого и последнего годаn – число лет. Найдем среднегодовую численность населения России за 2002-2007 г.г. по следующим данным: Таблица 4 Динамика численности населения России за 2002-2007 г.г.1
Среднегодовая численность населения с 2002 по 2007 г.г. в России равна:  В моментных рядах с неравноотстоящими периодами применяется средняя взвешенная арифметическая величина. 3.Аналитические показатели рядов динамики бывают базисные и цепные.Базисные- это когда последующие уровни сравниваются с одним уровнем, принятым за базисный уровень. Цепные- это когда последующие уровни сравниваютя с уровнями предыдущего периода. Аналитические показатели динамики бывают абсолютные приросты, коэффициенты и темпы роста , коэффициенты и темпы прироста; абсолютное значение одного процента прироста.( более подробно см. уч-к Ильина Г.Г. Статистические приемы и методы в рядах динамики», М.,РосНОУ,2004.С.88- 92. Средние величины аналитических показателей. Средняя геометрическая величина применяется в рядах динамики при расчете среднегодового коэффициента или темпа роста на базе цепных коэффициентов роста: 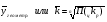 , где , где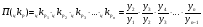 – произведение цепных коэффициентов роста – произведение цепных коэффициентов ростаn – число коэффициентов роста y – уровни ряда динамики Рассчитаем среднегодовой рост пенсионеров в России за 4 года (с 2004 по 2007 г.г.) по следующим данным: Таблица 3 Динамика численности пенсионеров (на конец года) в России1
Среднегодовой рост пенсионеров равен (среднегодовой темп роста): 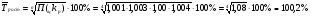 4.Метод приведения рядов динамики к сопоставимому виду. Так, на практике в рядах динамики встречаются случаи, когда одно и тоже явление по годам выражается в различных измерениях (например, переоценка имущества, уровень стоимости жизни и т.д.). Для изучения в целом рядов динамики за весь рассматриваемый период необходимо привести его к сопоставимому виду при помощи коэффициентов пересчета. Задача. Имеется динамика численности населения в N-м районе за семь лет в старых и новых границах. Требуется привести ряд динамики к сопоставимому виду (в новых границах). Таблица 7 Численность населения в N-м районе с 2002-2008 г.г. (тыс.чел.)
Решение: Предварительно определим коэффициент пересчета уровней в 2004 г., в котором произошло изменение границ: 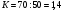 . .Умножая на этот коэффициент уровни ряда динамики в старых границах, получаем их сопоставимыми с уровнями в новых границах. В 2002 г. – 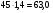 (тыс. чел.) (тыс. чел.)В 2003 г. –  (тыс. чел.) (тыс. чел.)Теперь получим сопоставимый ряд динамики. Таблица 8 Численность населения в N-м районе с 2002-2008 г.г. (тыс.чел.)
Подробно материал пунктов :6,7,8 изложен в уч. пос автора : « Статистические приемы и методы в маркетинге», с.98-106.
Рассмотрим на примере использование индексного метода. Задача. Имеются данные о цене и количестве реализуемых товаров 2-х видов за 2-а смежных квартала. Определите индексы цен, физического объема и стоимости, а также показать индексную и факторная взаимосвязь. Таблица 13 Расчет индексов цен, физического объема и стоимости
Решение: Прежде чем определить индексы, необходимо найти стоимость реализованной продукции за I-ый и II-ой кварталы, а также условную стоимость во II-м квартале при ценах I-го квартала (см гр.5, 6, 7 табл. 13). А теперь построим индексную и факторную взаимосвязь и сделаем выводы: Индексная связь  Фактическая взаимосвязь 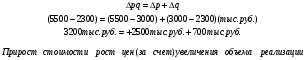 Таким образом, в отчетном периоде (II квартале) по сравнению с базисным (I квартал) стоимость реализованной продукции возросла на 139% ( 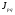 =2,39) за счет роста цен на 83% ( =2,39) за счет роста цен на 83% (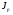 =1,83) и прироста объема реализованной продукции на 30% ( =1,83) и прироста объема реализованной продукции на 30% (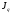 =1,3), что составило в абсолютном выражении прирост стоимости на 3200 тыс. руб., за счет роста цен прирост стоимости составил 2500 тыс. руб. и увеличилась стоимость реализованной продукции на 700 тыс. руб. за счет роста объема продукции; на сумму 2500 тыс. руб. произошел перерасход денежных средств у населения. =1,3), что составило в абсолютном выражении прирост стоимости на 3200 тыс. руб., за счет роста цен прирост стоимости составил 2500 тыс. руб. и увеличилась стоимость реализованной продукции на 700 тыс. руб. за счет роста объема продукции; на сумму 2500 тыс. руб. произошел перерасход денежных средств у населения.Надо отметить, что при построении индексов и изучении влияния изменения факторов на признак-результат не надо соблюдать последовательность факторов. Основным условием при формировании индексов надо знать, что при построении индексов качественного состава необходимо индексируемую величину взвешивать по весам отчетного (текущего) периода. Индексы количественного состава соизмеряются при помощи соизмерителей базисного периода ( 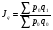 ). ). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

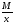 Количество реализованных единиц, кг
Количество реализованных единиц, кг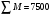
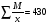


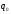


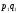
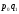
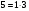
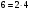

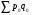 =2300
=2300 =5500
=5500