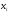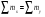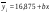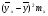Росноу Ильина Г.Г.Статистика Лекции. Курс лекций по статистике автор ильина г. Г.,к э. н., проф кафедры Финансы и банковское дело,росноу. Тема Общее понятие о статистике. План Общее понятие о статистике и о ее предмете. Основные категории статистики
 Скачать 0.63 Mb. Скачать 0.63 Mb.
|
|
Тема 8. Метод корреляционного анализа. План
1. Функциональные и корреляционные связи. Теория корреляции и её основные задачи. Одним из методов определения стохастической связи является метод корреляционного анализа. Слово «correlation» в переводе с английского языка означает взаимосвязь, соотношение, соответствие. Изучение зависимости вариации признака от окружающих условий, и составляет содержание теории корреляции1. В предыдущей 6-ой главе подробно рассматриваются детерминированные – функциональные связи. Однако, чаще в экономических исследованиях встрнечается вероятностные – стохастические зависимости, которые являются неточными, нестрогими. Корреляционная связь является частным случаем стохастической связи, как неполная, нежесткая связь. Итак, связи между изучаемыми явлениями бывают функциональные (детерминированными) и стохастическими (корреляционными). Функциональные связи – зависимости, при которой изменению каждого признака-фактора «х» соответствует изменение определенного признака-результата «y». Длина окружности четко зависит от длины радиуса. Корреляционные связи – зависимости, при которой изменению каждого признака-фактора «х» соответствует изменение ряда распределения признака-результата «y». Если при функциональной зависимости каждому значению факторного признака соответствует только одно значение результативного признака, то корреляционная зависимость появляется при большом числе наблюдений. При корреляционной связи устанавливается лишь тенденция изменения результативного признака при изменении факторного признака, т.е. результативный признак показывает, как в среднем он изменяется в зависимости от изменения признака фактора. Задачи корреляционного анализа. Основными задачами корреляции являются:
Первая задача корреляции решается при помощи расчета эмпирической линии регрессии (рассчитывается только для сгруппированных данных), теоретической линии регрессии (различные математические функции в зависимости от исходных данных). Вторая задача корреляции – определение тесноты связи при помощи r – коэффициента корреляции (применяется только при прямолинейной зависимости), ρ – эмпирическое корреляционное отношение для сгруппированных данных), η – теоретическое корреляционное отношение. 2. Виды корреляционной зависимости. Корреляционная связь классифицируется так же, как и функциональная (см. тему 6) по направлению зависимость и по аналитическому выражению. По направлению связи могут быть прямыми и обратными. Примером прямой связи может быть зависимость объема выпуска продукции от производительности труда. С ростом выработки растет выпуск продукции. А обратной связи – зависимость объема выпуска продукции от трудоемкости. Чем ниже трудоемкость, тем выше объем выпускаемой продукции. По аналитическому выражению связи бывают прямолинейными и криволинейными (см. более подробно тема 6 §2 стр. 51). Покажем на графике виды этих связей. 1-ый график. Связь прямая, прямолинейная y x 2-ой график. Связь обратная, прямолинейная y x 3-ий график. Связь прямая, криволинейная y x 4-ый график. Связь обратная, криволинейная y x Рис.1 Графическое изображение видов корреляционной зависимости 3. Графическое изображение корреляционной зависимости. В зависимости от исходных данных корреляция изображается по-разному. Для несгруппированных данных на поле координат наносятся общие точки. Точки не соединяются. Для сгруппированных данных на поле координат строится корреляционное поле. Несгруппированными данными называются такие, когда каждому признаку-результату «y» ставится в соответствие признак-фактор «х». Сгруппированными данными называются такие, когда каждому значению признака-результата «y» ставится в соответствие ряд распределения значений признака-фактора «х». Пример. Имеются 50 предприятий, которые сгруппированы по товарной продукции (тыс. руб.) и по производительности труда (руб./чел.). За признак-результат «y» принята товарная продукция за признак-фактор «х» - производительность труда. Товарная продукция «y» сгруппирована по 5 группам: 5-15, 15-25, 25-35, 35-45, св. 45. Производительность труда «х» сгруппирована по 4-м группам: до 7,5, 7,5-12,5, 12,5-17,5, св. 17,5. Изобразим графически связь между «х» и «y» в виде корреляционного поля. Точки, изображенные на поле корреляции обозначают общие предприятия имеющие ту или иную выработку и объем товарной продукции. Рассмотрим фрагментарно несколько предприятий:
Например, первое предприятие имеет объем товарной продукции 5 тыс. руб. и выработку – 2,6 руб./чел., значит общую точку надо поставить в общий клетке 5-15 по «y» и 2,5-7,5 по «х» и т.д. Всех точек будет 50 (сколько предприятий).
Рис.2 Корреляционное поле зависимости изменения товарной продукции от производительности труда. Поле корреляции не дает картины направления зависимости. Оно показывает, где точки сконцентрировались. На основании корреляционного поля составим корреляционную таблицу (см. табл. 14). Таблица 14 Корреляционная таблица зависимости товарной продукции (y) от производительности труда (х)
Для удобства расчета всех показателей выпишем из корреляционной таблицы необходимые расчетные показатели.     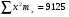 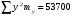   4. Показатели направления зависимости: эмпирическая линия регрессии (для сгруппированных данных), теоретическая линия регрессии. Эмпирическая линия регрессии показывает как в среднем изменяется признак-результат «y» в зависимости от изменения признака-фактора «х» при условии неизменности всех остальных факторов. Эмпирическая линия регрессии применяется только для сгруппированных данных, она равна:  Втором показателем направления зависимость является теоретическая линия регрессии, которая показывает как в среднем изменяется признак-результат «y» в зависимости от изменения признака-фактора «х» при полном исключении всех остальных факторов. Теоретическая линия регрессии строится по результатам математическим функциям в зависимости от исходных данных1. Теоретическая линия регрессии по прямой равна:  , где , гдеа – параметр, который показывает высоту графика и экономического смысла не имеет; b – коэффициент регрессии, который показывает, на сколько в среднем изменится признак-результат «y» при увеличении признака-фактора «х» на единицу измерения (то есть параметр b изучает направление признака-результата). Для определения параметров (а и b) необходимо решить систему нормальных уравнений. Для несгруппированных данных:  Для сгруппированный данных:  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||