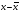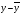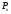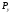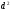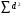Росноу Ильина Г.Г.Статистика Лекции. Курс лекций по статистике автор ильина г. Г.,к э. н., проф кафедры Финансы и банковское дело,росноу. Тема Общее понятие о статистике. План Общее понятие о статистике и о ее предмете. Основные категории статистики
 Скачать 0.63 Mb. Скачать 0.63 Mb.
|
|
Показатели направления зависимости для сгруппированных данных. Рассчитаем эти показатели для сгруппированных данных по данным корреляционной таблице. Значения эмпирической линии регрессии следующие: для 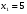 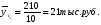 для 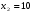 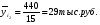 для 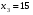 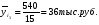 для 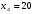 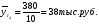 Нанесем эти значения на графики – на поле корреляции. Находим параметры (а и b) при помощи системы нормальных уравнений: 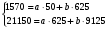 Получаем значение параметров: 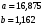 Коэффициент регрессии b показывает, что с увеличением производительности на 1 руб./чел., товарная продукция вырастает на 1,162 тыс. руб. Теоретическая линия регрессии равна: 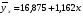 Значение теоретической линии регрессии такие: для 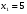 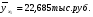 для 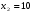 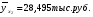 для 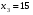 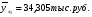 для 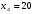 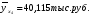 Нанесем на рисунок теоретическую линию регрессии. Показатели направления зависимости для несгруппированных данных. Рассчитаем показатель направления зависимости – теоретическую линию регрессии для несгруппированных данных. Для этого на основании таблицы 15 определим направление зависимости среднесуточного производства продукции «y» (тыс. руб.) от «х» - простоев (в % к календарному времени работы). Таблица 15 Зависимость среднесуточного производства продукции от простоев
Найдем параметры теоретической линии регрессии - 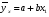 , при помощи решение системы нормальных уравнений. , при помощи решение системы нормальных уравнений. 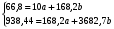 Получаем значение параметров: 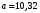 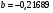 - коэффициент регрессии показывает, что с ростом простоев на 1% к календарному времени работы среднесуточное производство продукции снизилось на 0,21689 тыс. шт. или на 216,89 шт. - коэффициент регрессии показывает, что с ростом простоев на 1% к календарному времени работы среднесуточное производство продукции снизилось на 0,21689 тыс. шт. или на 216,89 шт.Теоретическая линия регрессии равна: 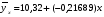 Значение теоретической линии регрессии такие: для: 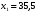 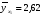 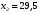 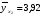 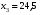 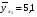 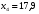 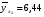 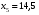 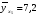 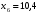 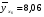 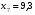 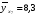 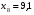 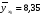 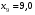 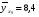 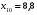 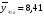 Надо отметить, что при выборе вида теоретической линии регрессии можно не только воспользоваться графическими изображениями эмпирических данных и эмпирическим путем определять вид направления зависимости, но и можно использовать метод конечных разностей между последующими и предыдущими вариантами. Так если первые разности между последующими и предыдущими вариантами одинаковы, т.е. 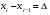 , то теоретическая линия регрессии выражается линейным уравнением , то теоретическая линия регрессии выражается линейным уравнением  . .Если вторые разности вариантов рядов распределения одинаковые, т.е. 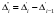 , то теоретическая линия регрессии выражается параболой второго порядка , то теоретическая линия регрессии выражается параболой второго порядка 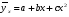 . Данное уравнения позволяет выявить не только скорость изменения вариантов «х», которую отражает коэффициент регрессии – «b», но и ускорение, которое учитывает параметр «с». . Данное уравнения позволяет выявить не только скорость изменения вариантов «х», которую отражает коэффициент регрессии – «b», но и ускорение, которое учитывает параметр «с».Для определения параметров a, b и с решаются следующие уравнения нормальных уравнений: Для несгруппированных данных: 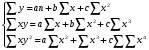 Для сгруппированных данных: 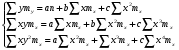 Надо отметить, что криволинейную тенденцию во многих случаях можно аппроксимировать при помощи параболы более высокого порядка: 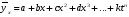 Существуют и другие методы при выборе формы уравнения1. 5. Показатели тесноты связи: коэффициент корреляции, эмпирическое корреляционное отношение (для сгруппированных данных), теоретическое корреляционное отношение (для сгруппированных и несгруппированных данных). Показатели тесноты связи показывают, какой удельный вес занимает признак-фактор «x» среди всех факторов, влияющих на признак-результат – «y». Они отвечают на вопрос: насколько необходимо изучение данной связи между признаками и целесообразности её практического применения, а также позволяет выявить наиболее значимые факторы, которые являются решающими при формировании результативного признака. Коэффициент корреляции2 r является показателем тесноты связи. Он измеряется так же и направление зависимости. Коэффициент корреляции равен: Для сгруппированных данных: 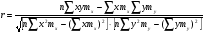 Для не сгруппированных данных: 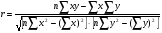 Если коэффициент корреляции принимает значение: - от 0 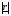 до 0,45, то связь между х и y – слабая до 0,45, то связь между х и y – слабая- от 0,4 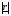 до 0,6, то связь между х и y – средняя до 0,6, то связь между х и y – средняя- от 0,6 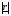 до 0,8, то связь между х и y – сильная до 0,8, то связь между х и y – сильная- от 0,8 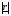 до 1 – очень тесная до 1 – очень теснаяКроме того, коэффициент корреляции, как указано выше, показывает направление зависимости. Если коэффициент корреляции принимает значение: от -1 до 0, то связь обратная. Если коэффициент корреляции принимает значение от 0 до 1 – то связь прямая. Если  = 0, то связь отсутствует, если = 0, то связь отсутствует, если  = 1, то связь функциональная. = 1, то связь функциональная.Коэффициент корреляции применяется только для прямолинейной связи. Эмпирическое корреляционное отношение – ρ, которое является универсальным показателем тесноты связи, так как применяется для прямо или криволинейной зависимости. Но в отличие от коэффициента корреляции, этот показатель не показывает направления связи. Он применяется только для сгруппированных данных. Эмпирическое корреляционное отношение равно: 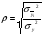 , где , где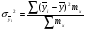 - дисперсия по эмпирической линии регрессии - дисперсия по эмпирической линии регрессии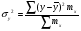 или или 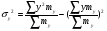 - общая дисперсия - общая дисперсияСтепень тесноты связи у эмпирического корреляционного отношения такая же как у коэффициента корреляции. При прямолинейной зависимости эмпирическое корреляционное отношение всегда будет немножко больше, чем абсолютное значение коэффициента корреляции. Теоретическое корреляционное отношение – 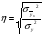 , где: , где:Для сгруппированных данных: 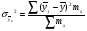 - дисперсия по теоретической линии регрессии - дисперсия по теоретической линии регрессииРасчет: 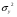 общая дисперсия см. выше общая дисперсия см. вышеДля несгруппированных данных: 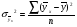 - дисперсия по теоретической линии регрессии - дисперсия по теоретической линии регрессии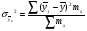 - дисперсия по теоретической линии регрессии - дисперсия по теоретической линии регрессии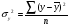 - общая дисперсия - общая дисперсияПоэтому, для несгруппированных данных теоретическое корреляционное отношение примет такой вид: 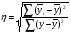 Теоретическое корреляционное отношение так же, как и эмпирическое корреляционное отношение является универсальным показателем, так как применяется при прямолинейной и криволинейной зависимости. Степень тесноты связи у теоретического корреляционного отношения такая же как у коэффициента корреляции и у эмпирического корреляционного отношения. При прямолинейной зависимости теоретическое корреляционное отношение будет всегда равно коэффициенту корреляции. А эмпирическое корреляционное отношение всегда будет незначительно больше теоретического корреляционного отношения. Рассмотрим показатели тесноты связи для сгруппированных данных. Для расчета воспользуемся корреляционной таблицей зависимости товарной продукции «y» от производительности труда «х» (см. табл. 14). Коэффициент корреляции равен: 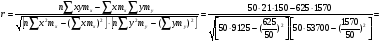 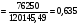 или 63,5%, т.е. связь между производительностью труда и товарной продукцией будет тесная, прямолинейная корреляционная, на 63,5% изменения товарной продукции зависят от изменения производительности труда, и на 36,5% - от других факторов (учтенных и не учтенных). или 63,5%, т.е. связь между производительностью труда и товарной продукцией будет тесная, прямолинейная корреляционная, на 63,5% изменения товарной продукции зависят от изменения производительности труда, и на 36,5% - от других факторов (учтенных и не учтенных).Эмпирическое корреляционное отношение равно: 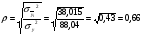 , где , где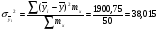 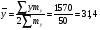 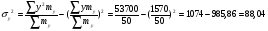 Таким образом, связь между производительностью труда и товарной продукцией будет тесная, корреляционная; на 66% изменение товарной продукции зависит от изменения производительности труда. Теоретическое корреляционное отношение равно: 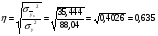 или 63,5% или 63,5%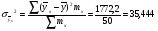 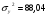 1 1Таким образом, связь между производительностью труда и товарной продукцией будет тесная, корреляционная; на 63,5% изменение товарной продукции зависит от изменения производительности труда. Мы видим, что 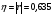 . .Далее рассчитаем показатели тесноты связи для несгруппированных данных на основе таблицы … Коэффициент корреляции равен: 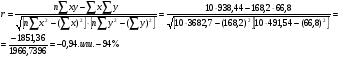 Связь между среднесуточным производством продукции и простоями будет обратная, довольно-таки тесная; т.е. на 94% среднесуточное производство зависит от снижения простоев, а на 6 % от других факторов. Теоретическое корреляционное отношение равно: 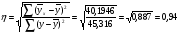 Таким образом, связь между среднесуточным производством продукции и простоями будет довольно таки тесная и на 94% среднесуточное производство зависит от простоев. 6. Простейшие показатели тесноты связи (коэффициент Фехнера, коэффициент корреляции рангов, коэффициент ассоциации). Рассмотрим ряд простейших показателей тесноты связи, которые приблизительно измеряют зависимости между признаком-фактором «х» и признаком-результатом «y». Коэффициент Фехнера (1801-1887 г.г.) измеряет тесноту связи по числу совпадений знаков отклонений индивидуальных величин от средней. Степень тесноты связи такая же как у коэффициента корреляции. Он равен: 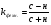 , где , гдес – число совпадений знаков отклонений индивидуальных значений от средней по признаку-фактору – «х» и признаку-результату «y». н – число несовпадений знаков отклонений. Этот показатель принимает значение от -1 до +1. Если знаки всех отклонений совпадут, то н = 0 и тогда 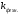 = +1, что говорит о возможном наличии прямой связи. = +1, что говорит о возможном наличии прямой связи.Если же знаки всех отклонений – разные, то с = 0 и 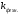 = -1, что говорит о возможном наличии обратной связи. Рассчитаем этот показатель (см. табл. 16). Рассчитаем средние величины по «х» и по «y». = -1, что говорит о возможном наличии обратной связи. Рассчитаем этот показатель (см. табл. 16). Рассчитаем средние величины по «х» и по «y».Таблица 16 Расчет коэффициентов Фенхера и корреляции рангов Спирмэна
Средняя списочная численность рабочих равна: 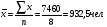 Средний объем товарной продукции равна: 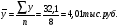 Затем находим отклонения от средних величин и посчитаем число совпадений и несовпадений знаков. Коэффициент Фехнера составит 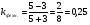 , что говорит о слабой связи прямой между списочной численностью и товарной продукцией. , что говорит о слабой связи прямой между списочной численностью и товарной продукцией.Этот показатель целесообразно использовать для установления факта наличия при небольшом объеме исходной информации. Коэффициент корреляции рангов Спирмэна равен: 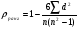 , где , где – количество рангов – количество рангов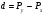 – разность между рангов – разность между ранговР – ранг (порядковые номера вариантов). Он варьирует от -1 до +1 и измеряет тесноту связи при небольшом количестве исходной информации и измеряет тесноту связи как между количественными, так и между качественными признаками при условии, что значение этих признаков могут быть проранжированны по степени убывания или возрастания. Коэффициент корреляции рангов Спирмена равен: 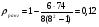 или 12% или 12%Теснота связи между признаком «x» и признаком «y» - слабая, прямая. Коэффициент ассоциации применяется для изменения тесноты связи для качественных альтернативных признаков. Он равен: 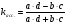 , где , гдеa – противоположно b c – противоположно d Расчетная таблица в этом случае состоит из четырех ячеек (таблица «четырех полей»), стратегическое сказуемое, которое схематически может быть представлено в следующем виде (см. табл. 17) Таблица 17 Расчетная таблица для коэффициента ассоциации
Коэффициент ассоциации равен: 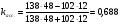 или 68,8% или 68,8%Данный показатель показывает частоту связи между показателями оценок, работающего по специальности и не по специальности. Связь между показателями будет тесная (68,8%), т.е. чем больше студенты будут работать по специальности, тем больше будет положительных оценок. 7. Методы оценки существенности расчета коэффициента корреляции. Как правило расчет коэффициента корреляции при определении тесноты связи производится на базе небольшого числа исходных данных – выборочных данных. В этой связи возникает необходимость оценить существенности коэффициента корреляции, которая дает возможность распространить выводы по результатам выборочных данных на генеральную совокупность. Критерии оценки существенности расчета коэффициента корреляции основаны на условии нормального распределения значений признака в генеральной совокупности. Рассмотрим некоторые из них: при большом объеме выборки и при малом объеме выборки. 7.1 При большом объеме выборки При большой выборке, отобранной из генеральной совокупности нормального распределения, предполагается считать распредение коэффициента корреляции близко к нормальному со средней, равной «r» и дисперсией 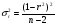 , а среднеквадратическая ошибка коэффициента корреляции тогда будет равна: , а среднеквадратическая ошибка коэффициента корреляции тогда будет равна: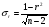 , где , гдеr – коэффициент корреляции выборочной совокупности; n – объем выборки; k = n – 2 – число степеней свободы при линейной зависимости. Если величина 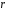 > >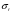 в в 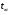 раз, или раз, или 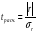 > >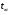 1 1Найдем для сгруппированных данных (см. таб. 14) среднюю квадратическую ошибку коэффициента корреляции: 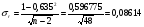 , тогда , тогда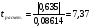 С вероятностью0,95 и числом степеней свободы k = 50 – 2 = 48, 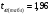 1. 1.Поскольку 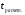 > >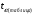 , следует, что с вероятностью Р = 0,95 и числом степеней свободы k = 48 можно утверждать о существенности выборочного коэффициента корреляции, т.е. связь между х и y – значимая. , следует, что с вероятностью Р = 0,95 и числом степеней свободы k = 48 можно утверждать о существенности выборочного коэффициента корреляции, т.е. связь между х и y – значимая.Для генеральной совокупности коэффициент корреляции будет находится в пределах. 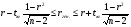 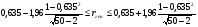 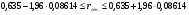 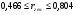 или 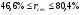 С вероятностью 0,95 можно утверждать, что коэффициент корреляции будет не ниже 46,6% и не выше 80,4%. 7.2 При малой выборки Для малого объема выборочной совокупности 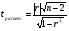 для оценки значимости коэффициента корреляции. для оценки значимости коэффициента корреляции.Если 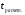 > >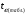 , то расчетный коэффициент корреляции существенен и связь между х и y вполне реальна. Если , то расчетный коэффициент корреляции существенен и связь между х и y вполне реальна. Если 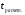 < <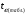 , то связь между х и y несущественна и корреляционная связь в генеральной совокупности отсутствует. , то связь между х и y несущественна и корреляционная связь в генеральной совокупности отсутствует.По данным таблицы 15 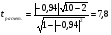 , а с вероятностью 0,95 и числом степеней свободы k = 10 – 2 = 8, , а с вероятностью 0,95 и числом степеней свободы k = 10 – 2 = 8, 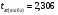 1. 1.Значит связь между х (простоями) и y – (выпуском продукции) существенна, т.к. 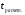 > >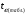 8. Проверка возможности использования прямолинейной функции – гипотезы Кендэла2 о линейной корреляционной зависимости. Для проведения гипотезы Кендэла о линейной зависимости определяется величина вероятности, которая рассчитывается по следующей формуле: 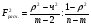 3, где 3, гдеn – объем совокупности m – число групп по признаку фактору х Если критерий 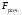 найденный с определенной вероятностью и критериями свободы ( найденный с определенной вероятностью и критериями свободы (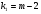 и и 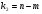 ) будут меньше F расчетного, то гипотеза о линейной связи между х и у отвергается. Если наоборот – то возможность использовать линейную функцию не опровергается. ) будут меньше F расчетного, то гипотеза о линейной связи между х и у отвергается. Если наоборот – то возможность использовать линейную функцию не опровергается.По данным таблицы 14 рассчитаем этот критерий. Критерий свободы 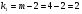 , а , а 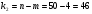 . С вероятностью . С вероятностью 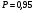 , , 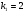 и и 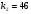 табличное значение табличное значение 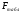 - критерия 1 = 3,2. - критерия 1 = 3,2.Расчетный критерий равен: 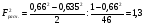 Поскольку 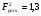 меньше меньше 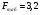 , то это не позволяет отклонить гипотезу о линейной связи между производительностью труда – х и товарной продукцией – y. , то это не позволяет отклонить гипотезу о линейной связи между производительностью труда – х и товарной продукцией – y.Вопросы для самопроверки
|

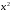
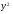
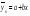
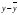
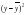
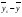
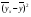
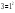
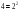
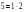
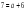
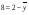
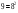
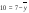
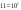
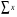 =168,2
=168,2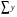 =66,8
=66,8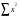
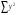 =491,54
=491,54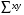 =938,44
=938,44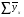
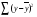 =45,316
=45,316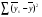 =40,1946
=40,1946