Росноу Ильина Г.Г.Статистика Лекции. Курс лекций по статистике автор ильина г. Г.,к э. н., проф кафедры Финансы и банковское дело,росноу. Тема Общее понятие о статистике. План Общее понятие о статистике и о ее предмете. Основные категории статистики
 Скачать 0.63 Mb. Скачать 0.63 Mb.
|
|
Тема 9. Выборочный метод. План
1. Общие понятия о выборочном методе и причины, вызывающие выборочное обследование. Приемы выборочного метода используется для более объективной оценки основных характеристик изучаемых явлений для более углубленного анализа изучаемого явления. При выборочном наблюдении изучается только часть совокупности, которая отбирается по определенным правилам, обеспечивающим беспристрастность отбора единиц. Эти правила основаны на законе больших чисел и теории вероятностей. Обобщающие показатели, полученные по отобранной части совокупности, распространяются на всю совокупность. Математическая статистика располагает методами анализа выборочных данных, при применении которых эти обобщающие показатели достаточно точно отражают, воспроизводят соответствующие показатели совокупности в целом. Это позволяет использовать выборочное наблюдение в следующих целях: – в случаях, когда изучаемая совокупность очень велика и поэтому не может быть практически охвачена сплошным наблюдением; – с целью экономии сил, средств и времени; – с целью расширения программы обследования – чем меньше отобранная часть, тем более детально ее можно изучить; – в случаях, когда изучение единиц совокупности сопровождается их порчей или уничтожением, например, при определении качества товаров (крепость ткани, нити, продолжительность горения электролампы). В экономике выборочное наблюдение применяется очень широко. Так, в промышленности оно применяется для контроля качества готовой продукции, в сельском хозяйстве – для определения урожайности, в торговле – для определения естественной убыли, установление конъюнктурного ассортимента товаров при проведении маркетинговых исследованиях. Генеральная и выборочная совокупности Вся совокупность, из которой производится отбор некоторого числа единиц для выборочного наблюдения, называется генеральной совокупностью. Часть генеральной совокупности, отобранная для обследования, называется выборочной совокупностью. Принятые условия обозначения выборки: N – объем генеральной совокупности n – объем выборочной совокупности  – средняя величина генеральной совокупности – средняя величина генеральной совокупности – генеральная доля, т.е. соотношение числа единиц m в генеральной совокупности обладающих данным значением признака ко всей численности генеральной совокупности – генеральная доля, т.е. соотношение числа единиц m в генеральной совокупности обладающих данным значением признака ко всей численности генеральной совокупности – выборочная доля, т.е. отношение числа единиц в выборочной совокупности обладающих данным значением признака ко всему объему выборки – выборочная доля, т.е. отношение числа единиц в выборочной совокупности обладающих данным значением признака ко всему объему выборки – среднеквадратичное в выборочном случайном отборе – среднеквадратичное в выборочном случайном отборе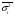 – средняя из внутригрупповых дисперсий для типичного отбора равна: – средняя из внутригрупповых дисперсий для типичного отбора равна:  - вероятность не появления события в генеральной совокупности - вероятность не появления события в генеральной совокупности - вероятность не появления события в выборочной совокупности - вероятность не появления события в выборочной совокупностиСредняя из противоположенных долей изучаемых явлений:  Средняя доля для типического отбора:  2. Условия правильности проведения выборочного отбора. Основное условие – случайность отбора, репрезентативность или представительность отбора. Ошибки репрезентативности могут быть систематическими и случайными. Случайные возникают в том случае, если выборочная совокупность недостаточно представительна. Систематические возникают при нарушении установленных правил отбора единиц. Величина случайных ошибок определяет надежность данных выборочных наблюдений, их пригодность для суждения о генеральной совокупности. При помощи формул теории вероятности можно рассчитать возможную максимальную случайную ошибку – вероятностный (стохастический) предел ошибки выборки (Δ). Максимально возможная (предельная) ошибка – это отклонение выборочной средней (или доли) от генеральной средней (доли). Ее величина зависит: – от степени колеблемости изучаемого признака генеральной совокупности – от способа формирования выборочной совокупности – от объема выборки. Ошибка репрезентативности представляет собой разность между показателями выборочной и генеральной совокупности: Для средней 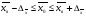 предельная ошибка выборки для средней 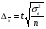 1 или 1 или 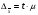 , где , где 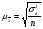 – средняя ошибка выборки для средней – средняя ошибка выборки для средней – стандартное отклонение – «коэффициент доверия», который зависит от вероятности, с которой гарантируется предельная ошибка вероятности. – стандартное отклонение – «коэффициент доверия», который зависит от вероятности, с которой гарантируется предельная ошибка вероятности.Для генеральной доли  предельная ошибка выборки для доли 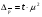 1, где 1, где  2 – средняя ошибка выборки для доли 2 – средняя ошибка выборки для долиПомимо ошибок репрезентативности существуют ошибки регистрации, которые свойственны для выборочного и сплошного наблюдения. Это ошибки, которые возникают вследствие недостаточной квалификации наблюдателя, неточности расчетов и несовершенством приборов. Таким образом, ошибки статистического наблюдения складываются из ошибок регистрации (сплошное и выборочное наблюдение) и ошибок репрезентативности (выборочное наблюдение). 3. Задачи выборки: – определение доверительных пределов, в которых находятся показатели генеральной совокупности (Δ) – определение доверительной вероятности того, что разность между показателями выборочной и генеральной совокупности не превзойдет наперед заданного числа: Р = F(t). F(t) – интеграл вероятности. – определение минимального объема выборки. Необходимо отобрать как можно меньше единиц выборки, но достаточное количество для данных условий (n) Виды отбора: – Повторный (по схеме возвращенного в урну шара) – Бесповторный (по схеме не возвращенного в урну шара) При повторном отборе численность единиц генеральной совокупности в процессе выборки остается неизменной. Ту или иную единицу, попавшую в выборку возвращают в генеральную совокупность, и она сохраняет равную возможность со всеми прочими единицами попасть в выборку при повторном отборе. При бесповторном отборе единица совокупности, попавшая в выборку не возвращается и при последующих отборах в выборке не участвует. Таким образом, при бесповторной выборке численности единиц генеральной совокупности сокращается в процессе исследования1. 4. Способы отбора Способы отбора определяют конкретный механизм отбора единиц из генеральной совокупности. По степени охвата единиц совокупности разделяют большие и малые выборки (с объемом  ). ).Наибольшее распространение получили следующие виды выборки: – собственно-случайная – механическая – типическая – серийная (гнездовая) Собственно-случайная выборка Случайным отбором называется такой отбор, при котором единицы из генеральной совокупности отбираются наудачу, по жребию. При этом каждая единица совокупности обладает одинаковой объективной возможностью быть отобранной. Таким образом, в отобранной части могут быть представлены единицы от всех частей генеральной совокупности, со всеми признаками, которые имеются у единиц генеральной совокупности. При таком отборе в средней выборочной  значения изучаемого признака будут представлены достаточно точно и, как принято говорить, выборочная совокупность будет репрезентативна генеральной совокупности то есть обобщающие характеристики выборочной совокупности будут близки к соответствующим характеристикам генеральной совокупности. значения изучаемого признака будут представлены достаточно точно и, как принято говорить, выборочная совокупность будет репрезентативна генеральной совокупности то есть обобщающие характеристики выборочной совокупности будут близки к соответствующим характеристикам генеральной совокупности.Но случайный отбор не следует понимать как беспорядочный отбор. Производя отбор, необходимо обеспечить соблюдение принципа случайности, организовать отбор так, чтобы его ошибки были действительно случайными. Случайный отбор может быть повторным и бесповторным. Механическая выборка При механическом отборе единицы для обследования отбираются уже не наудачу. При этой форме выборочного наблюдения единицы генеральной совокупности располагаются в каком-то порядке, но только не по изучаемому признаку, а, скажем, в алфавитном. Затем упорядоченная известным образом исходная совокупность делится на определенное число равных частей, и из каждой такой части отбирается одна единица – представитель с определенным порядковым номером (10-я, 20-я, 30-я). Например, при 10% выборке из совокупности в 1000 единиц она должна быть разделена на 100 равных частей, из которых могут быть отобраны 5-я, 15-я, 25-я и т.д. единицы.
Могут быть взяты и другие порядковые номера. Таким образом, если при случайном отборе есть лишь возможность попадания в выборку единиц от всех частей генеральной совокупности, то механический отбор направлен на то, чтобы обеспечить попадание в выборку таких представителей. В этом смысле, механический отбор можно назвать направленным отбором, и поэтому, при правильной организации, он репрезентативнее случайного отбора. Математическая статистика не располагает специальными зависимости для расчета средней ошибки выборки при механическом отборе, и она вычисляется по той же формуле, что и в условиях случайного бесповторного отбора. Следовательно, величина вычисленной таким образом средней ошибка механического отбора оказывается несколько завышенной. Типическая выборка Типический отбор также принадлежат к числу направленных видов отбора. При типическом отборе совокупность также разделяется на части, но не механически, а по каком-то типическому признаку. Например, для обследования бюджетов рабочих все рабочие данного предприятия предварительно группируются по профессиям, т.е. по признаку, который определяет уровень заработной платы. Затем из каждой группы производят случайный или механический отбор. При типическом отборе обеспечивается попадание в выборку представителей всех типических групп, что повышает репрезентативность выборочных данных. Типичные группы могут быть как равными, так и не равными по численности. В последнем случае отбор производится пропорционально объему каждого типа во всей генеральной совокупности. Типический отбор бывает повторным и бесповторным. Серийная (гнездовая) выборка Серийный (гнездовой) отбор заключается в том, что отбору подвергается совокупность не отдельных единиц, а серий или групп их. При этом внутри групп обследуются все единицы, без исключения. В сельскохозяйственной статистике, где отбираемые серии хозяйств называют «гнездами», этот вид отбора получил название гнездового. Отбор серий может быть организован как случайный, так и механический. Серийный отбор бывает повторный и бесповторный. Рассмотрим основные типы задач согласно задачам выборочного метода1. Случайный отбор 1-ый тип задач – Определение предельной ошибки выборки. Для случайного повторного отбора (для средней) Задача. С вероятностью 0,9973 определить в каких пределах находится средний срок изделий в генеральной совокупности ( 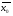 ), если отобрано 250 деталей, из которых средний срок службы 41,9 месяца ( ), если отобрано 250 деталей, из которых средний срок службы 41,9 месяца ( ) и среднеквадратическое отклонение ) и среднеквадратическое отклонение  = 6,2 месяца. = 6,2 месяца.Дано:  2 2Решение:   Вывод: С вероятностью 0,9973 можно утверждать, что средний срок службы изделий в генеральной совокупности находится в пределах от 40,7 до 43,1 месяца. Для случайного повторного отбора (для доли) Задача. С вероятностью 0,9973 определить в каких пределах находится в генеральной совокупности доля изделий срок службы которых превышает 50 месяцев, если доля изделий, срок службы которых превышает 50 месяцев в выборочной совокупности равна 0,124, отобрано 250 изделий. Дано:  Решение:   Вывод: С вероятностью 0,9973 можно утверждать, что доля деталей в генеральной совокупности срок службы которых превышает 50 месяцев составляет не менее 6,1% и не более 18,7%. Таблица 18 Предельная ошибка выборки и объем выборки при различных видах отбора
Для случайного повторного отбора (для средней) Задача. При испытании на крепость отобраны в случайном порядке 400 отрезков пряжи одиночной нити (основа – 65 кордная) были получены следующие результаты1: Таблица 19 Расчет основных выборочных характеристик (  и и  ). ).
Определите с вероятностью 0,97 среднюю крепость пряжи во всей партии. Для определения основных характеристик (  и и  ) выборочной совокупности необходимо найти графы с 3-ей по 6-ую в таблице 19. ) выборочной совокупности необходимо найти графы с 3-ей по 6-ую в таблице 19.Выборочная средняя крепость пряжи равна:  Выборочная дисперсия составляет:  Итак, на основе следующих данных определим среднюю крепость пряжи во всей партии. Дано: 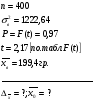 1 1Решение:  Тогда средняя крепость пряжи во всей партии будет находиться в следующих пределах:  Вывод: С вероятностью 0,97 можно утверждать, что средняя крепость во всей пряжи в генеральной совокупности будет не менее 195,6 гр. и не более 203,2 гр. Доля случайного повторного отбора (для доли) Задача. По данным предыдущей задачи с вероятностью 0,97 найти доля образцов пряжи во всей партии с крепостью выше 185 гр. Дано:  2 2Решение:  доля образцов пряжи во всей партии с крепостью. доля образцов пряжи во всей партии с крепостью.Вывод: С вероятностью 0,97 можно утверждать, что доля образцов во всей партии в генеральной совокупности с крепостью выше 185 гр. находятся в пределах  . .2-ой тип задач – Определение вероятности того, что предельная ошибка выборки не превышает заданной величины. Случайный повторный отбор Задача. С какой вероятностью можно утверждать, что выборочная доля бракованных деталей будет отличатся от генеральной доли не более чем на 1%, если при измерении 115 деталей установлена доля брака равная 0,5%? Дано:  Решение: Знаем, что:  тогда  , а вероятность , а вероятность 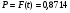 (по таблице F(t))1 (по таблице F(t))1Вывод: С вероятностью 0,8714 можно утверждать, что выборочная доля бракованных деталей будет отличаться от генеральной доли не более чем на 1%. 3-ий тип задач – Определение минимального объема выборки Случайный бесповторный отбор. Задача. Сколько следует проверить деталей для установления процента годности, чтобы с вероятностью 0,9973 ожидать отклонения выборочной доли от генеральной, не превышающей 5%. По прежним испытаниям 98% годовых деталей предлагается проводить через бесповторный отбор, объем генеральной совокупности N = 5000 шт. деталей. Дано:  2 2Решение:  Вывод: Следует проверить не менее 70 образцов деталей, чтобы с вероятностью 0,9973 можно ожидать отклонения выборочной доли от генеральной, не превышающей 5%. Механический отбор имеет формулу предельной ошибки выборки для случайного бесповторного отбора. Типический бесповторный отбор (для средней) 2-ый тип задач – определение вероятности того, что предельная ошибка выборки не превзойдет наперед заданного числа. Задача. В магазине 3-х различных типов произведено обследование среднедневной выработки 10% продавцов. По каждому типу магазинов в случайном порядке была взято по 100 продавцов каждого типа. Причем: – в магазине 1-го типа среднедневная выработка одного продавца оказалась равной 650 руб. при среднеквадратичном отклонении 50 руб. – в магазине 2-го типа среднедневная выработка одного продавца – 600 руб. при среднеквадратичном отклонении – 30 руб. – в магазине 3-го типа соответственно 575 руб. и 45 руб. Какова вероятность утверждения, что среднедневная выработка всех продавцов, обследованных в магазинах, не будет больше или меньше среднедневной выработки продавцов, попавших в выборку на 1,75 руб. Дано: 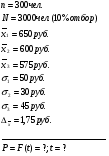 Решение:  , где , где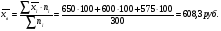   1 1Вывод: С вероятностью 0,5467 можно утверждать, что среднедневная выработка всех продавцов, обследованных в магазинах не будет более 1,75 руб. Типический бесповторный отбор (для средней) 1-ый тип задач – определение генеральной средней (предельной ошибки выборки) Задача. С вероятностью 0,9973 найти среднедневную выборку рабочих 2-х профессий слесарей и токарей в генеральной совокупности. Проведен 10% отбор. Имеются следующие данные: Таблица 201 Расчет основных выборочных характеристик.
Таблица 21 Расчет общей средней и средней из частных дисперсий.
Выборочная среднедневная выработка рабочих равна:  , где среднедневная выработка: , где среднедневная выработка:– слесарей  – токарей  Выборочная средняя из внутригрупповых дисперсий равна:  , где внутригрупповая дисперсия: , где внутригрупповая дисперсия:– слесарей  – токарей 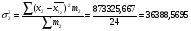 Итак, на основе следующих данных определим среднедневную выработку рабочих (слесарей и токарей) в генеральной совокупности. Дано:  1 1Среднедневная выработка рабочих в генеральной совокупности находится в следующих пределах: 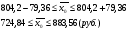 , где предельная ошибка выборки составляет: , где предельная ошибка выборки составляет: Типический бесповторный отбор (для доли) Задача. При обследовании семейных бюджетов города была организованна 10%-ая типическая выборка, результаты которой представлены следующим образом.
С вероятностью 0,6832 (t = 1 по табл.) установите границы доли расходов на оплату жилья населения города? Решение: средняя доля выборки равна:  Предельная ошибка доли составит:  Тогда, доля расходов на оплату жилья в генеральной совокупности находится в следующих пределах:  Таким образом, доля расходов на оплату жилья в генеральной совокупности будет не менее 4,8% и не более 8,6% от семейных бюджетов. Вопросы для самопроверки.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


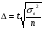



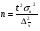


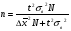



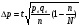



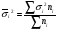








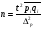





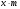
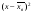

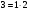



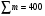
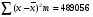
 рабочих по дневной выборке (руб.)
рабочих по дневной выборке (руб.) слесарей (чел.)
слесарей (чел.)











 рабочих (чел.)
рабочих (чел.)


