ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ПЛОСКИХ СЕЧЕНИЙ
К геометрическим характеристикам попереченных сечений относятся:
- статические моменты площади сечения (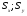 ) )
- осевые моменты инерции (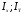 ) )
- центробежный момент инерции (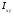 ) )
- полярный момент инерции ( ) )
- моменты сопротивления (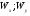 ) )
- радиусы инерции (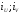 ). ).
Рассмотрим поперечное сечение бруса в системе координат х0у.
Выделим элементарную площадку dA координатами х и у.
На основании теоремы Вариньона (из курса теоретической механики):
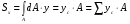
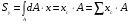
Где 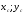 - координаты центра тяжести фигуры. - координаты центра тяжести фигуры.
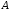 - площадь фигуры. - площадь фигуры.
Статический момент равен сумме произведений элементарных площадок на расстояние от центра тяжести этих площадок до оси, относительно которой он подсчитывается.
Статический момент измеряется в 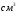 или или 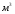 . (-), (+), (=0). . (-), (+), (=0).
При параллельном переносе осей значения статических моментов не остаются постоянными, а изменяются и могут иметь как положительное, так и отрицательное значение.
Это значит, что среди семейства параллельных осей существует единственная ось, относительно которой статический момент равен нулю.
Ось, относительно которой статический момент равен нулю, называется центральной.
Точка пересечения центральных осей называется центром тяжести сечения.
Статический момент инерции применяется для определения координат центр тяжести простых и сложных фигур:
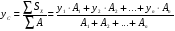
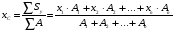
Осевой момент инерции равен сумме произведений элементарных площадок на квадрат расстояния от центра тяжести этих площадок до оси, относительно которой подсчитывается:
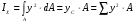

Измеряется в 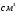 , , 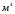 , (+). , (+).
Центральный момент инерции – момент инерции, взятый относительно центральной оси.
Главные центральные оси – оси, исходящие из центра тяжести всей фигуры.
Если всю фигуру или ее часть перемещать вдоль оси, то значение момента инерции не изменится.
Центробежный момент инерции – равен сумме произведений элементарных площадок до осей, относительно которых он подсчитывается:
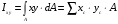
 Если одна из осей сортамента является осью симметрии, то в этом случае центробежный момент инерции равен 0. Если одна из осей сортамента является осью симметрии, то в этом случае центробежный момент инерции равен 0.
При повороте осей на 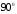 центробежный момент инерции меняет свой знак на противоположный. центробежный момент инерции меняет свой знак на противоположный.
Измеряется в 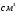 , , 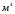 , (+), (-), (=0). , (+), (-), (=0).
Полярный момент инерции равен сумме осевых моментов инерции:
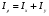
Полярным моментом инерции называется момент инерции относительно оси, проходящей через полюс  под прямым углом к плоскости фигуры: под прямым углом к плоскости фигуры:
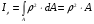
Измеряется в 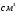 , , 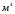 , (+). , (+).
Моменты инерции относительно параллельных осей
Пусть моменты инерции  относительно осей относительно осей 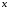 и и 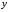 , проходящих через центр тяжести фигуры, нам известны. , проходящих через центр тяжести фигуры, нам известны.
Необходимо определить моменты инерции относительно новых осей  и и 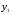 , проходящих параллельно осям , проходящих параллельно осям 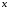 и и 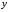 на расстоянии на расстоянии 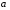 и и 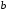 . .
Найдем, например, момент инерции относительно новой оси  : :

Во втором слагаемом  , т.к. ось , т.к. ось 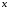 проходит через центр тяжести фигуры, тогда: проходит через центр тяжести фигуры, тогда:
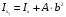
аналогично

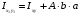
Следовательно, момент инерции относительно произвольной оси равен моменту инерции относительно центральной оси, проведенной параллельно данной, плюс произведение площади фигуры на квадрат расстояния между осями.
Центробежный момент инерции равен центробежному моменту инерции относительно центральных осей плюс произведение площади данной фигуры на расстояния между параллельными осями.
Моменты инерции при повороте осей
Будем считать, что моменты инерции относительно осей 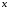 и и 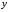 , проходящих через центр тяжести фигуры, нам известны. , проходящих через центр тяжести фигуры, нам известны.
Необходимо определить моменты инерции относительно новых осей  и и 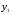 , проходящих под углом , проходящих под углом  к осям к осям 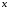 и и 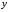 . .
При повороте осей координаты точек меняются по формулам:
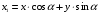 и и 
Относительно новых осей формулы моментов инерции имеют вид:
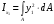 , ,  , , 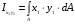
Подставив и проинтегрировав значения  и и 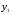 , получим: , получим:
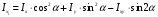

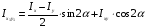
Главные оси и главные моменты инерции
Понятие о радиусе инерции
Главными осями инерции плоской фигуры называются оси, отвечающие следующим требованиям:
Они должны проходить через центр тяжести все фигуры.
Относительно этих осей моменты инерции должны иметь экстремальный значения.
Центробежный момент инерции относительно этих осей всегда равен нулю.
Главными моментами инерции – моменты инерции определяемые относительно
главных осей.
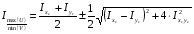
Угол поворота главных осей инерции:
Для этого необходимо: 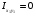 , ,
тогда 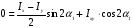 тогда тогда 
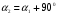 , т.е. существуют две взаимно перпендикулярные оси. , т.е. существуют две взаимно перпендикулярные оси.
Радиусы инерции определяются по формулам:
Эллипс, построенный на полуосях равных радиусам инерции, называется эллипсом инерции.
Эллипс инерции строят для того, чтобы можно было судить о жесткости поперечного сечения. Радиус инерции всегда больше центра тяжести.
Моменты сопротивления: 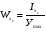 ; ; 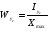
 - расстояние от центра тяжести всей фигуры до наиболее удаленных точек. - расстояние от центра тяжести всей фигуры до наиболее удаленных точек.
Моменты инерции сложных фигур
В расчетной практике часто приходится вычислять моменты инерции сложных сечений относительно различных осей, лежащих в плоскости фигуры.
Для стандартных поперечных сечений стержней – уголков равнополочных и неравнополочных, двутавровых сечений и т.д. – моменты инерции относительно различных осей даны в таблице ГОСТ. В этих таблицах также даны площади сечений, положения центров тяжести и другие характеристики.
При вычислении моментов инерции сложных сечений их можно разбить на отдельные простые фигуры, моменты инерции которых известны.
Дальнейший расчет ведут в следующем порядке:
Определяют положение центра тяжести сечения, а следовательно, и главных центральных осей.
Вычисляют (или берут из ГОСТ) значения моментов инерции отдельных частей сечения относительно собственных центральных осей, которые параллельны главным центральным осям всего сечения.
Вычисляют моменты инерции частей, составляющих сечение, относительно его главных центральных частей.
Определяют главные центральные моменты инерции всего сечения путем суммирования для каждой из главных осей величин.
Таким образом, при вычислении моментов инерции составных
сечений пользуются правилом: момент инерции сечения относительно данной оси равен сумме моментов инерции составляющих это сечение частей относительно той же оси.
Это правило вытекает из известного свойства определенного интеграла:
Интеграл суммы нескольких слагаемых равен сумме интегралов этих слагаемых.
Условие и порядок выполнения работы
Вычертить в масштабе заданное поперечное сечение балки на миллиметровой бумаге, провести все вспомогательные оси. Выписать из ГОСТов требуемые величины и размеры, привязав их к центральным осям каждой фигуры выполненного чертежа. Основные размеры проставить также на чертеже.
Определить положение центра тяжести всей фигуры, применив для этого статические моменты плоских фигур. В качестве вспомогательных осей целесообразно выбрать центральные оси одной из фигур. Провести на чертеже через найденный центр тяжести параллельно прежним осям центральные оси все фигуры.
Найти осевые моменты инерции и центробежный момент инерции всей фигуры относительно ее центральных осей.
Определить моменты сопротивления фигуры относительно этих центральных осей.
Найти положение главных центральных осей фигуры и провести их на чертеже. На чертеже показать также угол поворота главных центральных осей инерции по отношению к прежним осям и его направление.
Найти моменты сопротивления фигуры относительно главных центральных осей инерции. При этом расстояние от осей до наиболее удаленных точек фигуры допускается определять графически.
Определить радиусы инерции фигуры относительно главных центральных осей и по ним построить эллипс инерции.
Произвести проверку расчетов.
Исходные данные для решения задания (вариант) берутся из табл. 1.
Таблица 1 |
 Скачать 3.9 Mb.
Скачать 3.9 Mb.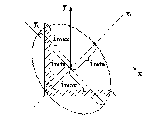
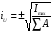

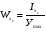 ;
; 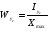
 - расстояние от центра тяжести всей фигуры до наиболее удаленных точек.
- расстояние от центра тяжести всей фигуры до наиболее удаленных точек.
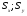 )
)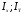 )
)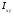 )
) )
)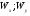 )
)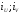 ).
).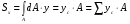
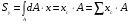
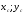 - координаты центра тяжести фигуры.
- координаты центра тяжести фигуры.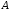 - площадь фигуры.
- площадь фигуры.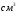 или
или 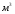 . (-), (+), (=0).
. (-), (+), (=0).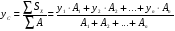
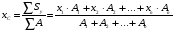
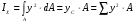

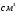 ,
, 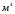 , (+).
, (+).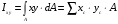
 Если одна из осей сортамента является осью симметрии, то в этом случае центробежный момент инерции равен 0.
Если одна из осей сортамента является осью симметрии, то в этом случае центробежный момент инерции равен 0.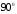 центробежный момент инерции меняет свой знак на противоположный.
центробежный момент инерции меняет свой знак на противоположный.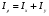
 под прямым углом к плоскости фигуры:
под прямым углом к плоскости фигуры: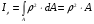
 относительно осей
относительно осей 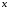 и
и 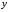 , проходящих через центр тяжести фигуры, нам известны.
, проходящих через центр тяжести фигуры, нам известны. и
и 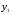 , проходящих параллельно осям
, проходящих параллельно осям 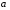 и
и 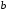 .
.
 , т.к. ось
, т.к. ось 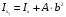

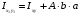
 к осям
к осям 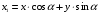 и
и 
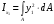 ,
,  ,
, 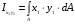
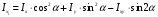

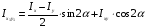
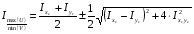
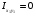 ,
, 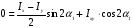 тогда
тогда 
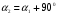 , т.е. существуют две взаимно перпендикулярные оси.
, т.е. существуют две взаимно перпендикулярные оси.