Курс лекций с вариантами заданий для выполнения расчетнографических работ студентами очного и заочного факультета всех специальностей

• Название: Курс лекций с вариантами заданий для выполнения расчетнографических работ студентами очного и заочного факультета всех специальностей
• Анкор: metodichka_zaochnikam_1_chast_2014 (2).docx
• Дата: 15.03.2017
• Размер: 3.9 Mb.
• Имя файла: metodichka_zaochnikam_1_chast_2014 (2).docx
• Тип: Курс лекций; #3824
• страница: 8 из 9

4. ИЗГИБ. СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ
БАЛКИ И РАМЫ

Лекция № 6

Изгиб. Расчет статически определимых балок и рам. Определение ВСФ и напряжений при изгибе.

1. 
   Общие понятия о деформации изгиба.
   
2. 
   Типы опор балок.
   
3. 
   Правило знаков для изгибающих моментов и поперечных сил.
   
4. 
   Зависимость между изгибающим моментом, поперечной силой и интенсивностью распределения нагрузки.
   
5. 
   Условие прочности по нормальным напряжениям.
   
6. 
   Условие прочности по касательным напряжениям.
   
7. 
   Потенциальная энергия деформации при изгибе.
   

Общие понятия о деформации изгиба
Изгиб – вид деформации, когда в поперечных сечениях стержня возникают изгибающие моменты, т.е. внутренние моменты, плоскость действия которых перпендикулярна плоскости поперечного сечения стержня.

При действии такой нагрузки ось стержня искривляется.
Данный вид нагружения называется изгибом, а стержни, работающие на изгиб – балками.

Изгиб подразделяется на 4 вида: чистый, поперечный, прямой, косой.

Изгиб называется чистым, если изгибающий момент является единственным внутренним усилием, возникающим в поперечном сечении стержня.

Поперечный изгиб – если в поперечных сечениях стержня вместе с изгибающим моментом возникают также и поперечные силы.

Прямой изгиб – если плоскость действия изгибающего момента (силовая плоскость) проходит через одну из главных из центральных осей поперечного сечения стержня.

Косой изгиб – если плоскость действия изгибающего момента не совпадает ни с одной из главных осей сечения.
Типы опор балок
Опоры балок, рассматриваемые как плоские системы, бывают 3 основных типов:

1. 
   Шарнирно-подвижная опора
   

Такая опора не препятствует вращению конца балки и его перемещению вдоль плоскости качения. В ней может возникать только одна реакция, которая перпендикулярна плоскости качения и проходит через центр катка.

2. 
   Шарнирно-неподвижная опора
   

Такая опора допускает вращения конца балки, но устраняет поступательное перемещение ее в любом направлении. Возникающую в ней реакцию можно разложить на две составляющие – горизонтальную и вертикальную.

3. 
   Жесткая заделка или защемление
   

Такое закрепление не допускает ни линейных, ни угловых перемещений опорного сечения. В этой опоре может в общем случае возникать реакция, которую обычно раскладывают на две составляющие (вертикальную и горизонтальную) и момент защемления (реактивный момент).

Консоль или консольная балка – балка с одним заделанным концом.

Балка статически определимая – если опорные реакции могут быть найдены из числа уравнений статики.

Балка статически неопределимая – если число неизвестных опорных реакций больше, чем число уравнений статики возможных в данной задаче.

Для определения реакций в таких балках приходится составлять дополнительные уравнения – уравнения перемещений.
Правило знаков для изгибающих моментов и поперечных сил
Поперечная сила Q в сечении балки считается положительной, если равнодействующая внешних сил слева от сечения направлена внизу вверх, а справа – сверху вниз.

Изгибающий моментМ в сечении балки считается положительным, если в рассматриваемом сечении балка изгибается выпуклостью вниз.
Правило знаков при изгибе
!!!Момент считается «+», если слева от сечения направлен против часовой стрелки, а справа по часовой.

Если балка прогибается выпуклостью вниз, то эпюра моментов будет «+»

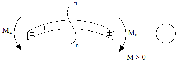Момент считается «+», если слева от сечения направлен против часовой стрелки, а справа по часовой. Если балка прогибается выпуклостью вниз, то эпюра моментов будет «+»
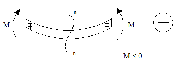	Поперечная сила Q «+», если эпюра моментов восходящая слева направо.
	Поперечная сила Q «-», если эпюра моментов восходящая справа налево.

Зависимость между изгибающим моментом, поперечной силой и

интенсивностью распределенной нагрузки

Рассмотрим балку, нагруженную произвольной нагрузкой. Определим поперечную силу в сечении, стоящем от левой опоры на расстоянии 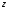. Спроецировав на вертикаль все силы, расположенные левее сечения, получим: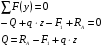



Аналогично вычислим поперечную силу в смежном сечении, расположенном на расстоянии 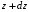от левой опоры: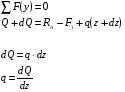



Производная от поперечной силы по абсциссе сечения балки равна интенсивности распределенной нагрузки.

Вычислим теперь изгибающий момент в сечении с абсциссой 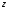, взяв сумму моментов сил, приложенных слева от сечения. Для этого распределенную нагрузку на участке длиной 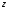заменим ее равнодействующей, равной 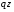и приложенной в середине участка, на расстоянии от сечения: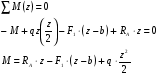


Аналогично вычислим изгибающий момент в смежном сечении, стоящем от левой опоры на расстоянии

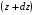
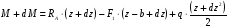(2)

Вычитая из (1) – (2), получим:



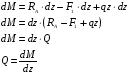
т.е. производная от изгибающего момента по абсциссе сечения балки равна поперечной силе (теорема Журавского).

Взяв производную от обеих частей равенства, получим:



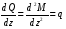
т.е. вторая производная от изгибающего момента по абсциссе сечения балки равна интенсивности распределенной нагрузки.

Все полученные зависимости будем использовать в дальнейшем главным образом при построении эпюр поперечных сил и изгибающих моментов.
Условие прочности по нормальным напряжениям
Для обеспечения прочности балки необходимо, чтобы наибольшие растягивающие и наибольшие сжимающие напряжения при изгибе в опасном сечении, т.е. в сечении, где 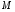имеет наибольшее значение, не превосходили соответствующих допускаемых напряжений: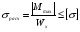



Величина 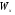называется осевым моментом сопротивления или моментом сопротивления при изгибе.

Значения 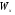для простейших фигур у нас есть в таблицах ГХПС.

Для прокатных сечений (двутавры, швеллера и т.п.) значения 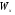указаны в таблицах сортаментов.

Для подбора сечения балки из выше написанного уравнения получим зависимость:



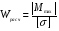
Найдя по этой формуле допускаемый изгибающий момент и зная связь между моментом и нагрузкой (по построенной эпюре моментов) можно определить допускаемую нагрузку.
Условие прочности по касательным напряжениям
- формула Журавского
Закон распределения по сечению касательных напряжений для балки прямоугольного сечения определяются законом изменения 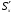, т.к. остальные величины для данного сечения постоянны, причем .

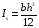Статический момент относительно оси 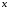равен: .
Потенциальная энергия деформации при изгибе
Потенциальную энергию изгиба, равную работе внутренних сил, взятую с обратным знаком, можно определить по формуле:



В общем случае изгиба в поперечных сечениях балки кроме изгибающих моментов возникают еще и поперечные силы.

Как показывают исследования поперечная энергия сдвига невелика и ею обычно пренебрегают.

Поэтому данная формула пригодна и для чистого, и для общего случая изгиба.
Лекция № 7

Расчет на прочность.

Метод допускаемых напряжений и разрушающих нагрузок.

1. 
   Допускаемые напряжения.
   
2. 
   Расчет на прочность по допускаемым напряжениям.
   
3. 
   Расчет на прочность по разрушающим нагрузкам.
   

Допускаемые напряжения
В результате испытаний на растяжение (сжатие) можно получить основные данные о механических свойствах материала. Рассмотрим, как можно полученные результаты применить в практических расчетах инженерных конструкций на прочность.

Детали машин и других конструкций должны удовлетворять условиям прочности и жесткости. Размеры деталей необходимо подбирать такими, чтобы под действием приложенных нагрузок они не разрушались и не получали деформаций, превышающих допускаемые. В большинстве деталей машин остаточные деформации, как правило, не допускаются.

Заметные остаточные деформации появляются в пластичных материалах, когда напряжения достигают предела текучести 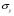. Разрушение наступает, когда напряжения достигают величины предела прочности 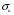; при этом деформации хрупкого материала могут быть незначительными.

Итак, для деталей, изготовленных из пластичного материала, опасным напряжением можно считать предел текучести ; для деталей из хрупкого материала – предел прочности .

Естественно, что эти напряжения не могут быть приняты в качестве допускаемых. Их следует уменьшить настолько, чтобы в эксплуатационных условиях действующие напряжения всегда были меньше предела пропорциональности.

Таким образом, допускаемое напряжение может быть определено по формуле:



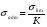
где 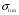- опасное (предельное) напряжение

- нормативный коэффициент запаса прочности (т.е. предписываемый нормами проектирования и конструирования).
Выбор величины коэффициента запаса прочности зависит от состояния материала (хрупкое или пластичное), характера приложения нагрузки (статическая, динамическая или повторно-переменная) и некоторых общих факторов, имеющих место в той или иной степени во всех случаях.

К этим факторам относятся:

1. Неоднородность материала и, следовательно, различие его механических характеристик в образцах и реальных деталях.

2. Неточность задания величин внешних нагрузок.

3. Приближенность расчетных схем и некоторая приближенность расчетных формул.

4. Учет конкретных условий работы рассчитываемой конструкции.

5. Метод определения напряжений (степень точности этого метода).

6. Долговечность и значимость проектируемого сооружения или машины.

Эти факторы учитывает коэффициент запаса прочности , который иногда называют основным.

Коэффициент определяется опытным путем.

В каждой области техники уже сложились свои традиции, свои требования, свои методы и специфика расчетов, в соответствии с которыми и назначается коэффициент запаса прочности.

Величина нормативного коэффициента запаса прочности регламентируется для строительных конструкций - СНиП, для машиностроительных – внутриотраслевыми заводскими нормами.

Величина запаса прочности зависит от того, какое напряжение считается опасным.

Для пластичных материалов в случае статической нагрузки опасным напряжением, как уже сказано следует считать предел текучести, т.е.

, а , тогда: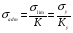



где 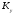- коэффициент запаса прочности по отношению к пределу текучести.

На основании данных длительной практики конструирования, расчета и эксплуатации машин и сооружений, величина коэффициента запаса прочности 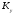для сталей при статической нагрузке принимается равной .

Для хрупких материалов при статических нагрузках опасное напряжение – предел прочности, т.е.

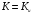, а , тогда: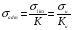

где 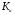- коэффициент запаса прочности по отношению к пределу прочности.
Величину коэффициента запаса прочности для хрупких материалов обычно принимают равной от 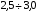. Допускаемые напряжения, получаемые по этой формуле, обычно называют основными допускаемыми напряжениями в связи с тем, что предел прочности определить проще, чем предел текучести.

Поэтому иногда и для пластичных материалов при определении допускаемых напряжений исходят из величины предела прочности, пользуясь формулой:



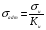
В этом случае, учитывая, что 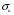превышает 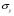на 50-70%, коэффициент запаса прочности 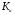для пластичных материалов принимают равным .

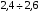Расчет на прочность по допускаемым напряжениям предполагает выбор нормативного коэффициента запаса прочности , который выбирается из таблиц, составляемых на основании большого числа экспериментальных исследований.

Однако иногда размеры конструкции или детали уже известны (заданы из эксплуатационных или других требований).

В этом случае расчетным путем определяют фактический коэффициент запаса прочности . Для этого рассчитывают в опасном сечении детали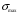

и, зная для материала детали предельное напряжение 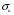или 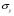, определяют фактический коэффициент запаса:

- для хрупких материалов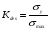

- для пластичных материалов

Затем расчетный и нормативный коэффициенты сравнивают между собой, и дается заключение о работоспособности конструкции.

Выбор величины допускаемых напряжений очень важен, т.к. от правильного установления их значений зависят прочность и безопасность проектируемых конструкций, а также экономичность расчета.

Ориентировочные величины основных допускаемых напряжений, принятые в настоящее время для наиболее распространенных материалов, приводятся в справочной литературе.

Конечной целью расчета любой конструкции является использование полученных результатов для оценки пригодности этой конструкции к эксплуатации при минимальных затратах материала.
Расчет на прочность по допускаемым напряжениям
Расчет на прочность по допускаемым напряжениям основан на оценке прочности материала в опасной точке. При таких расчетах наибольшие нормальные напряжения в опасном сечении и в опасной точке сравниваются с допускаемыми напряжениями.

Если наибольшие напряжения, которые возникают в конструкции, не превышают допускаемых, то считается, что необходимый запас прочности обеспечен.

Такой способ расчета на прочность называют расчетом по допускаемым напряжениям.

Условие прочности бруса, работающего на осевое растяжение (сжатие), имеет вид:



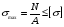
где 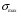- наибольшее по абсолютному значению нормальное напряжение в брусе, т.е. напряжение в опасном сечении.

Данное условие прочности позволяет производить три вида расчета на прочность:

1. 
   Проверка прочности. По известным нагрузкам (а, следовательно, и внутреннему усилию в опасном сечении конструкции) и размерам поперечного сечения определяют наибольшее рабочее напряжение и сравнивают его с допускаемым напряжением для данного материала. Расчет выполняется непосредственно по этой формуле.
   
2. 
   Подбор сечения. По найденному внутреннему усилию от заданной нагрузки и допускаемому напряжению применяемого материала определяют требуемую площадь поперечного сечения.
   
3. 
   Определение допускаемых нагрузок (несущей способности). По известным поперечным размерам детали или элемента конструкции и допускаемому напряжению материала устанавливают значение допускаемых нагрузок.
   

Метод расчета на прочность по допускаемым напряжениям, бесспорно, обеспечивает прочность конструкции, но во многих случаях не позволяет рационально использовать все ее возможности и часто приводит к завышению ее массы.

При расчете по допускаемым напряжениям опасным (или предельным) состоянием конструкции считается такое, при котором наибольшее напряжение, хотя бы в одной точке материала конструкции достигает опасной величины – предела текучести (для пластичного материала) или предела прочности (для хрупкого материала). Состояние всей остальной массы материала. Во внимание не принимается.

Между тем при некоторых видах сопротивления (кручении или изгибе) при неравномерном распределении напряжений по поперечному сечению и в статически неопределимых конструкциях, изготовленных из пластичных материалов, появление напряжений, равных пределу текучести, в большинстве случаев не является опасным для всей конструкции.

Практика показывает, что при появлении местных пластических деформаций конструкция еще может удовлетворять заданным эксплуатационным требованиям и для ее перехода в предельное состояние необходимо дальнейшее возрастание нагрузки.

Это обстоятельство учитывает другой расчет на прочность по разрушающим нагрузкам.
Расчет на прочность по разрушающим нагрузкам
Данный метод предполагает определение расчетным путем не напряжений, а максимальной нагрузки, которую может выдержать конструкция, не разрушаясь и не претерпевая непрерывно нарастающих пластических деформаций.

При этом в качестве условия прочности необходимо выполнение требования, чтобы наибольшая нагрузка не превышала допускаемого значения, т.е.

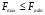
Допускаемая нагрузка, в свою очередь, определяется отношением:



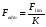
где 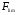- предельная (разрушающая) нагрузка

- коэффициент запаса прочности.

Нагрузка называется разрушающей, если после ее приложения система утрачивает свою грузоподъемность.

Коэффициент запаса прочности назначается из тех же соображений, что и при расчете по допускаемым напряжениям.

Идею метода расчета по разрушающим нагрузкам высказал в 1904 г. русский ученый и инженер, специалист в области железобетонных конструкций А.Ф.Лолейт.

В основу данного метода положено условие предельного равновесия.

При расчете конструкций из пластичных материалов – это условие, предусматривающее одновременное достижение состояния текучести для всей конструкции в целом.

Площадку текучести имеют диаграммы растяжения малоуглеродистых сталей и некоторых других материалов.


Например, кривая на диаграмме растяжения алюминия (рис.б) за пределом пропорциональности (за пределом действия закона Гука) имеет очень слабый наклон, и при расчетах ее можно принять за горизонтальную прямую.

Для того чтобы упростить расчеты, диаграммы растяжения, сжатия и чистого сдвига для пластичных материалов схематизируют так, что прямая закона Гука непосредственно соприкасается с горизонтальной прямой без плавного перехода
Этим самым принимается равенство между пределами пропорциональности 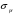и пределом текучести .

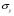Длина горизонтального участка диаграммы не ограничивается, т.е. материал считается не упрочняющим, а идеально пластичным. Такая диаграмма называется диаграммой Прандтля.

Указанная схематизация достаточно точна для материалов типа алюминия и вполне допускаема для материалов, имеющих диаграммы с ограниченной площадкой текучести
Так, при наличии подобных площадок величина деформации в начале упрочнения 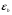в несколько раз превышает величину деформации 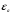в начале появления пластической деформации.

Поэтому даже при неравномерном распределении напряжений (изгиб, кручение), но дальнейшем распространении пластической зоны с выравниванием напряжений предела текучести они достигнут одновременно по всему сечению раньше, чем начнется упрочнение материала в точках с наибольшей пластической деформацией.

Таким образом, предельное состояние, обусловленное значительной пластической деформацией, наступит до начала упрочнения материала, и разрушающая нагрузка может быть определена по пределу текучести.

Все теоретические соображения неоднократно проверялись экспериментом, причем, всегда наблюдалось достаточно близкое совпадение величин предельной (разрушающей) нагрузки, определенной экспериментально и расчетным путем.
Условия и порядок выполнения задач

1. 
   Для заданных схем статически определимых балок определить:
   

• 
  опорные реакции и построить эпюры поперечных сил и изгибающих моментов;
  
• 
  на эпюрах должны быть проставлены числовые значения величин в характерных точках.
  

Для каждого участка балки необходимо:

• 
  записать уравнения определяемых величин и вычислить их значения для характерных точек.
  

2. 
   В задаче 4 дополнительно:
   

• 
  из условия прочности подобрать стальную балку двутаврового сечения;
  
• 
  вычислить для этой балки максимальные значения нормального и касательного напряжений;
  
• 
  в опасных сечениях построить эпюры изменения нормальных и касательных напряжений по высоте двутавровой балки;
  
• 
  определить прогибы в характерных точках балки (середина пролета, точки приложения сил, крайние точки на консолях);
  
• 
  по найденным точкам построить изогнутую ось балки. Вычислить также угол поворота сечения на правой опоре.
  

Чертежи балок выполняются в произвольном масштабе.

3. 
   В задаче 4^а из условия прочности подобрать балку прямоугольного сечения из древесины при отношении высоты к ширине (h:b=4:1). Допускаемое нормальное напряжение для древесины принять равным 10 МПа. Исходные данные (вариант) для решения задач берутся из табл. 4.
   

Таблица 4

Исходные данные к задаче - 4, 4^а, 4^б

Вариант	Заданная нагрузка			Длины участков, м
	F, кН	q, кН/м	М, кНм	a	в	с
1	12	4	15	2,2	1,5	1,0
2	16	6	16	2,4	1,6	1,1
3	18	8	18	2,5	1,8	1,2
4	20	10	20	2,6	2,0	1,3
5	22	12	22	2,8	2,1	1,4
6	25	14	25	3,0	2,2	1,5
7	26	16	26	3,2	2,4	1,6
8	28	18	28	3,4	2,5	1,7
9	30	20	30	3,5	2,6	1,8
10	32	22	32	3,8	2,8	1,9

Задача 4. Двухопорная балка

1		2
3		4
5		6
7		8
9		10

Задача 4 (продолжение)

11		12
13		14
15		16
17		18
19		20

Задача 4 (окончание)

21		22
23		24
25		26
27		28
29		30

Задача 4^а. Консольная балка

1		2
3		4
5		6
7		8
9		10

Задача 4^а. Консольная балка

11		12
13		14
15		16
17		18
19		20

Задача 4^а. Консольная балка

21		22
23		24
25		26
27		28
29		30

Задача 4^б. Двухопорная балка

1		2
3		4
5		6
7		8
9		10

Задача 4^б. Двухопорная балка

11		12
13		14
15		16
17		18
19		20

Задача 4^б. Двухопорная балка

21		22
23		24
25		26
27		28
29		30

Пример решения задачи 4

Определить и построить эпюры: крутящих моментов - М_кр, поперечных сил Q, подобрать сечение двутавра.

1. 
   Определение опорных реакций
   

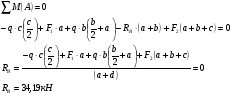
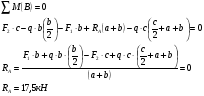
Проверка

2. 
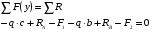
   Определение внутренних силовых факторов методом сечений
   

	Сечение I-I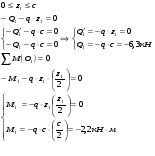
	Сечение II-II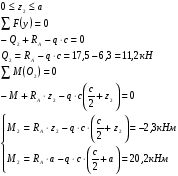
		Сечение III – III
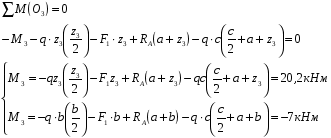		Сечение IV-IV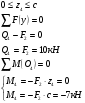
		Сечение V-V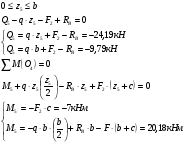

3. 
   Подбор сечения двутавровой балки
   

,


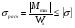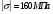
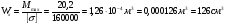
№ 16






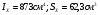
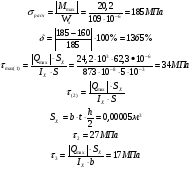
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ