Курс лекций с вариантами заданий для выполнения расчетнографических работ студентами очного и заочного факультета всех специальностей
 Скачать 3.9 Mb. Скачать 3.9 Mb.
|
2. РАСТЯЖЕНИЕ ПРЯМЫХ СТЕРЖНЕЙОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ Лекция № 3
Внешние силы (нагрузки), действующие на конструкцию Нагрузки, действующие на сооружения и их элементы, представляют собой силы или пары сил (моменты), которые могут рассматриваться как сосредоточенные или распределенные. Расчетная схема В природе сосредоточенных сил не бывает. Все реальные силы – это силы, распределенные по некоторой площади или объему. Например, давление колеса на рельс практически передается через небольшую площадку, которая получается в результате деформации рельса и колеса. Поэтому, для определения внутренних сил, возникающих в рельсе и колесе на некотором расстоянии от площади передачи давления, можно распределенную нагрузку заменить сосредоточенной равнодействующей силой. Это упростит расчет. Сосредоточенные нагрузки выражаются в Н, кН, МН (ньютонах, килоньютонах, меганьютонах). Распределенные нагрузки могут быть поверхностными (например, давление воды или ветра на стенку) или объемными (например, сила инерции, сила тяжести тела). Выражаются распределенные нагрузки в отношении единицы силы к единице длины (кН/м). И сосредоточенные и распределенные нагрузки могут быть как статическими, так и динамическими. Статическими называются нагрузки, которые будучи приложены к элементу возрастают постепенно от нуля до своей конечной величины так, что их действие не вызывает ускорений в элементах конструкций. (Собственный вес моста). Динамическими называются нагрузки, изменяющиеся во времени с большой скоростью. (Ударные, переменные и др.). Действие таких нагрузок сопровождается возникновением колебаний сооружений. Законы изменения нагрузок во времени могут иметь весьма сложный характер. В частном случае, изменение нагрузки F может носить периодически повторяющийся характер, так что через одни и те же промежутки времени t максимальные значения нагрузки будут повторяться. Нагрузки такого типа называются нагрузками с установившимся режимом или повторно-периодическими. Но во многих случаях изменение нагрузки во времени не имеет установившегося характера. Это нагрузки, действующие на детали автомобилей, станков, тракторов. Также нагрузки, действующие на сооружения (дома, мачты и т.п.) от давления ветра, снега. Такие нагрузки называют повторными нагрузками неустановившихся режимов. Глубокое изучение таких нагрузок возможно лишь с помощью методов статики и теории вероятности, которые применяются для изучения случайных величин. Деформации и перемещения Как было отмечено, все тела под действием приложенных к ним внешних сил в той или иной степени деформируются, т.е. изменяют свои формы или размеры, либо то и другое одновременно. Изменение линейных размеров тела или его частей называется линейной деформацией, а изменение угловых размеров – угловой деформацией. При этом увеличение размеров тела называется удлинением, а уменьшение размеров – укорочением. Если деформация изменяется по объему тела, то говорят о деформации в данной точке тела, в определенном направлении. Если на поверхности тела вблизи исследуемой точки нанести весьма малый прямоугольник 1234, то в результате деформации этот прямоугольник в общем случае примет вид параллелограмма 1’2’3’4’. Длины сторон прямоугольника изменятся (увеличатся или уменьшатся), а стороны повернутся по отношению к первоначальному положению. Если, например, длина стороны 23 изменится на величину 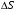 , то отношение , то отношение  называется средней линейной деформацией (в данном случае средним удлинением в точке 2). называется средней линейной деформацией (в данном случае средним удлинением в точке 2).При уменьшении отрезка S в пределе получим:  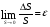 Где величина 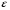 называется истинной линейной деформацией (в точке 2 в направлении 23). называется истинной линейной деформацией (в точке 2 в направлении 23).Изменение первоначального прямого угла между сторонами рассматриваемого прямоугольника 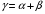 будет характеризовать угловую деформацию (или угол сдвига) в данной точке. будет характеризовать угловую деформацию (или угол сдвига) в данной точке.Опыты показывают, что деформации, как линейные, так и угловые могут после снятия нагрузки или полностью исчезнуть, или исчезнуть лишь частично (в зависимости от материала и величины нагружения). Деформации, исчезающие после разгрузки тела, называются упругими, а свойство тел принимать свою первоначальную форму после разгрузки – упругостью. Деформации, сохраняемые телом и после удаления нагрузки, называются остаточными или пластическими, а свойство материалов давать остаточные деформации называется пластичностью. Для нормальной эксплуатации сооружения принимаются условия жесткости:
Понятие о внутренних силах (метод сечений). Внутренние силовые факторы. Под действием внешних нагрузок в поперечных сечениях элементов конструкций и деталей машин возникают внутренние силы упругости, характеризующие связи между молекулами и его отдельными частицами. Возникновение внутренних сил сопровождается деформацией материала. Эти силы противодействуют внешним силам и стремятся восстановить прежнюю форму тела. Одна из задач сопротивления материалов состоит в определении величин внутренних сил. Для этого широко используется метод сечений, сущность которого заключается в следующем:
Если внешние силы лежат в одной плоскости, то для их уравновешивания необходимо в общем случае приложить в сечении три внутренних усилия: - силу N, направленную вдоль оси стержня и называемую продольной силой; - силу Q, действующую в плоскости поперечного сечения и называемую поперечной силой; - внутренний момент М, плоскость действия которого перпендикулярна плоскости сечения. Этот момент возникает при изгибе стержня и называется внутренним изгибающим моментом. После этого составляют уравнения равновесия для отсеченной части тела, из которых и определяют N, Q, M. Если же внешние силы, к которым относятся также реакции опор, не лежат в одной плоскости (пространственная задача), то в поперечном сечении в общем случае могут возникнуть 6 внутренних усилий, которые являются компонентами главного вектора силы и главного момента системы внутренних сил Для определения этих шести усилий необходимо использовать шесть уравнений равновесия:   и и 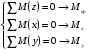 где  - крутящий момент. - крутящий момент.На рисунке принята правовинтовая система координат, причем ось z совмещена с осью стержня. В частном случае в поперечном сечении стержня могут возникать: 1. Только продольная сила N. Этот случай нагружения называется растяжением (если сила N направлена от сечения) или сжатием (если сила N направлена к сечению). 2. Только поперечная сила 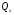 или или 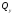 . Это случай сдвига, среза, смятия, изгиба. . Это случай сдвига, среза, смятия, изгиба.3. Только крутящий момент Т. Это случай кручения. 4. Только изгибающий момент 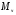 или или  . Это случай изгиба. . Это случай изгиба.5. Несколько усилий, например, изгибающий и крутящий моменты. Это случаи сложных видов деформаций (или сложного сопротивления). Если число неизвестных усилий равно числу уравнений равновесия, то задача называется статически определимой. Если же число неизвестных усилий больше числа уравнений равновесия – статически неопределимой. Пример метода сечений
Решение Для определения усилий в стержнях АВ и ВС применим метод сечений. Проведем сечение а-а по стержням, отбросив левую часть, и рассмотрим равновесие правой части. Усилие в обоих стержнях предположим растягивающими, направленными от узла и обозначим их 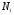 и и 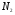 . .Составим уравнения равновесия отсеченной части системы: 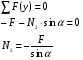 и и 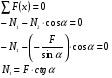  Напряжения Было отмечено, что в поперечном сечении стержня действуют не сосредоточенные внутренние усилия N, Q, T и т.д., а непрерывно распределенные силы, интенсивность которых может быть различной в разных точках сечения и в разном направлении. Как же измерить интенсивность внутренних сил в данной точке данного сечения, например в т. А? Выделим вокруг точки А малую площадку  . .Пусть 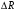 - равнодействующая внутренних сил, действующих на эту площадку. - равнодействующая внутренних сил, действующих на эту площадку.Тогда, среднее значение внутренних сил, приходящихся на единицу площади 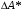 рассматриваемой площадки, будет равно рассматриваемой площадки, будет равно Эта величина называется средним напряжением. Она характеризует среднюю интенсивность внутренних сил. Уменьшая размеры площади в сечении, получим: 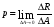 Эта величина называется напряжением в данной точке данного сечения. Напряжением называется внутренняя сила, приходящаяся на единицу площади в данной точке данного сечения. Измеряется в 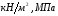 . .Полное напряжение  можно разложить на две составляющие: можно разложить на две составляющие:
Касательное напряжение в зависимости от действующих сил может иметь любое направление в плоскости сечения. Для удобства касательное напряжение представляют в виде двух составляющих по направлению координатных осей. Растягивающее нормальное напряжение считается положительным, сжимающее – отрицательным. Обозначение касательных напряжений снабжены двумя индексами: - первый из них указывает, какой оси параллельна нормаль к площадке действия данного напряжения; - второй – какой оси параллельно само напряжение. Разложение полного напряжения на нормальное и касательное имеет определенный физический смысл: нормальное напряжение возникает, когда частицы материала стремятся отдалиться друг от друга или, наоборот, сблизиться. 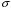 - возникает при растяжении, сжатии, изгибе и сложном напряженном состоянии. - возникает при растяжении, сжатии, изгибе и сложном напряженном состоянии.Касательные напряжения связаны со сдвигом частиц материала по плоскости рассматриваемого сечения. 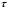 - возникает при кручении, срезе, сдвиге и изгибе. - возникает при кручении, срезе, сдвиге и изгибе.Совокупность напряжений на всех элементарных площадках, которые можно провести через какую-либо точку тела, называется напряженным состоянием в данной точке. Если по граням кубика действуют только одни нормальные напряжения, то они называются главными, а площадки, на которых они действуют, называются главными площадками. Можно доказать, что в каждой точке напряженного тела существуют три главные взаимно-перпендикулярные площадки. Различные виды напряженного состояния классифицируются в зависимости от числа возникающих главных напряжений. Если отличны от нуля все три главных напряжения, то напряженное состояние называется трехосным или объемным. Если равно нулю одно из главных напряжений, то напряженное состояние называется двухосным или плоским. Если равны нулю два главных напряжения, то напряженное состояние называется одноосным или линейным. Зная напряженное состояние в любой точке детали, можно оценить прочность этой детали. В простейших случаях оценка прочности элементов конструкции производится или по наибольшему нормальному напряжению или по наибольшему касательному напряжению. Так, что условие прочности записывается в виде: 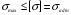 или или  где 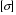 , , 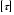 - допускаемые напряжения, которые зависят от материала и условий работы рассматриваемого элемента. - допускаемые напряжения, которые зависят от материала и условий работы рассматриваемого элемента.Эти величины выбираются с таким расчетом, чтобы была обеспечена нормальная эксплуатация конструкция. В более сложных случаях оценка прочности производится по приведенному напряжению в соответствии с той или иной гипотезой прочности. Лекция № 4 Растяжение (сжатие) прямого стержня
Растяжение и сжатие – это простой и часто встречающийся случай напряженного состояния элементов конструкции и деталей машин. В таких условиях работает буксировочный канат или трос подъемного механизма, колонна здания. Чистое (центральное) растяжение или сжатие возникает в элементе конструкции, если внешняя нагрузка вызывает в нем только одно внутреннее усилие, которое сопротивляется этой внешней нагрузке, - нормальную продольную силу. При определении значений внутренних нормальных сил, действующих в поперечных сечениях стержней, примем следующее правило знаков: - нормальная сила положительна, если сопротивляется растяжению стержня; - нормальная сила отрицательна – если сопротивляется сжатию. Для определения значений внутренней нормальной силы в любом из поперечных сечений используется метод сечений. Пусть прямой стержень постоянной толщиной в одном конце закреплен, а к его другому торцу приложена растягивающая его вдоль оси стержня внешняя сила F. Какое по величине внутреннее продольное усилие возникает в некотором поперечном сечении стержня n-n? Прежде всего, отметим, что под действием закрепления и внешней силы стержень растягивается (деформируется), но никуда не движется, т.е. остается в равновесии. Удобно вначале мысленно «снять» со стержня закрепление. Заменим его влияние на стержень эквивалентно действующей внешней силой. Эта сила равна реакции закрепления. Т.е. в закреплении возникает некоторое усилие, благодаря которому верхний край стержня остается неподвижным. Это усилие называют реакцией закрепления на внешнюю нагрузку, передающееся на это закрепление через деформируемый стержень. Незакрепленный стержень, теперь уже под действием двух внешних воздействий: известной силы и неизвестной пока реакции также никуда не движется, т.е. находится в равновесии. Определить величину реакции поможет математическая формулировка этого факта. Проведем координатную ось Оz, для удобства совпадающую с осью стержня. Стержень никуда не движется под действием силы и реакции в частности, не движется и вдоль оси, потому что проекции этих внешних сил на ось уравновешивают друг друга. Такого рода факт в механике формулируется уравнением общего равновесия стержня: суммарная проекция на ось Оzвсех действующих на стержень внешних сил, равна нулю: 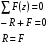 При построении уравнений общего равновесия механики принято использовать следующее правило знаков:
Эпюры – графики внутренних усилий, напряжений, перемещений, деформаций, возникающих в элементах конструкций и деталях машин под воздействием внешней нагрузки. Напряжения при растяжении (сжатии) прямого стержня Предположим, растягивающую брус внешнюю силу удалось распределить равномерно по его торцам. Опыты показывают. Что в этом случае каждое продольное волокно бруса подвержено только растяжению и в любом его поперечном сечении внутренние силы действуют только по нормали к этим сечениям. Поперечные сечения бруса, плоские до деформации, под действием внешних сил перемещаются параллельно своему начальному положению и остаются постоянными. Растягивающие стержень внешние силы не всегда удается распределить по площади стержня равномерно. Но опыты показывают, что поведение поперечных сечений растягиваемых стержней, расположенных на некотором расстоянии от места приложения внешней нагрузки, уже не зависит от способа приложения этих сил и всегда соответствует гипотезе плоских сечений. При рассмотрении деформаций растяжения или сжатия, а также при рассмотрении последующих простых деформаций нами будет рассматриваться принцип Сен-Венана, названный по имени французского ученого XIX века, который заключается в том, что внутренние силовые факторы, возникающие в результате действия внешних сил, распределяются по сечениям рассматриваемого тела равномерно. Рассмотрим стержень, подверженный действию продольных сил Если на поверхность призматического стержня нанести сетку линий параллельных и перпендикулярных оси стержня, и приложить к нему растягивающую силу, то можно убедиться в том, что линии сетки и после деформации останутся взаимно-перпендикулярными, но расстояние между ними изменятся. Все горизонтальные линии, например, cd, переместятся вниз, оставаясь горизонтальными и прямыми. Можно предположить, что и внутри стержня будет происходить то же самое, т.е. поперечные сечения стержня плоские и нормальные к его оси до деформации, останутся плоскими и нормальными к оси и после деформации. Эту гипотезу называют гипотезой плоских сечений (гипотезой Бернулли). Продольная сила N есть равнодействующая нормальных напряжений в поперечном сечении: 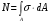 поскольку поскольку  , то , то , отсюда , отсюда 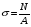 В частном случае, когда на стержень действует одна внешняя сила, из уравнения равновесия получим: 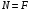 И вместо общей формулы получим частный вид формулы для растяжения: 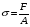 Эти формулы справедливы и для сжатия, с той только разницей, что сжимающие напряжения считаются отрицательными. Кроме того, сжатые стержни помимо расчета на прочность рассчитываются также и на устойчивость. Очевидно, что эти напряжения в реальных условиях нельзя создавать больше или много меньше определенной величины. Поэтому вводится понятие допускаемого напряжения: 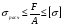 - условие прочности. - условие прочности.Определение деформаций и перемещений. Закон Гука. Опыты показывают, что при растяжении длина стержня увеличивается, а поперечные размеры уменьшаются, при сжатии – наоборот. Для многих материалов при нагружении до определенных пределов опыты показали следующую зависимость между относительным удлинением стержня 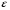 и напряжением и напряжением 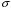 : : , где , где  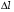 - абсолютное удлинение стержня - абсолютное удлинение стержня - длина образца до деформации - длина образца до деформации - длина образца после деформации - длина образца после деформацииЭта зависимость носит название закона Гука и формулируется следующим образом: линейные деформации прямо пропорциональны нормальным напряжениям. 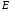 - коэффициент, зависящий от материала, т.е. его способность сопротивляться деформированию. Он характеризует жесткость материала, т.е. его способность сопротивляться деформированию. - коэффициент, зависящий от материала, т.е. его способность сопротивляться деформированию. Он характеризует жесткость материала, т.е. его способность сопротивляться деформированию.Для ст.3  . .Для других материалов значение 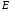 можно найти в справочниках. можно найти в справочниках.Имея ввиду, что для стержня постоянного сечения:   , а , а 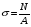 Можно получить формулу для определения полного (абсолютного) удлинения (укорочения) стержня: 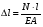 Между продольным удлинением 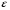 и поперечным существует зависимость: и поперечным существует зависимость: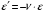 Здесь  - коэффициент поперечной деформации (коэффициент Пуассона),который характеризует способность материала к поперечным деформациям. - коэффициент поперечной деформации (коэффициент Пуассона),который характеризует способность материала к поперечным деформациям.При пользовании этой формулой удлинение считается положительным, а укорочение – отрицательным. Для всех материалов 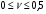 . .Для стали при упругих деформациях можно принимать 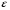 =0,3. =0,3.Зная 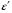 можно определить полное поперечное сужение или расширение стержня можно определить полное поперечное сужение или расширение стержня 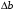 : : 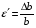 , где , где 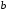 - поперечный размер стержня до деформации - поперечный размер стержня до деформации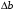 - поперечный размер стержня после деформации. - поперечный размер стержня после деформации.В стержнях переменного сечения напряжения в поперечных сечениях можно считать распределенными равномерно (если угол конусности 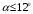 ) и определять их по той же формуле, что и для стержня постоянного сечения. ) и определять их по той же формуле, что и для стержня постоянного сечения.Для определения деформаций стержня переменного сечения, в поперечных сечениях которого действует продольная сила N, найдем сначала удлинение  элемента длиной элемента длиной  , которое является дифференциалом полного удлинения , которое является дифференциалом полного удлинения 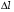 . .Согласно закону Гука, имеем: 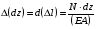 Полное удлинение стержня получим, интегрируя выражение в пределах 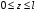 : :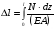 , если , если 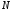 и и 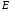 - величины постоянные, то - величины постоянные, то Чтобы воспользоваться этой формулой, необходимо знать закон изменения 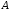 в зависимости от в зависимости от 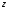 . .Для ступенчатых стержней интегрирование заменяется суммирование, и полное изменение длины бруса определяется как алгебраическая сумма деформаций его отдельных частей, в пределах которых  : : Например, для стержня изображенного на схеме, имеем:  Определим теперь удлинение стержня постоянного сечения под действием силы тяжести, которая представляет собой нагрузку, равномерно распределенную вдоль стержня. Удельный вес материала обозначим через  . .Рассмотрим деформацию элемента  , выделенного на расстоянии , выделенного на расстоянии 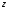 от нижнего конца. от нижнего конца.Удлинение элемента равно: 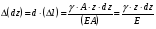 Интегрируя это выражение в пределах, получим  Это выражение можно представить в другом виде, если учесть, что сила тяжести бруса равна: 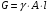 или или  , тогда получим , тогда получим 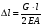 - формула по определению перемещения с учетом собственного веса при известной длине - формула по определению перемещения с учетом собственного веса при известной длинеСледовательно, удлинение бруса постоянного сечения от собственной силы тяжести в два раза меньше удлинения от действия силы, равной силе тяжести и приложенной к его концу. Опытное изучение свойств материалов Для изучения свойств материалов и установления значения предельных (по разрушению или по пластическим деформациям) производят испытания образцов материала вплоть до разрушения. По виду деформации различают испытания на растяжение, сжатие, кручение и изгиб. Испытания производят при статической и ударной (испытание на усталость и выносливость) нагрузках на ГМС – 50. Цель испытания на растяжение – определение механических характеристик материала. При проведении испытания автоматически записывается диаграмма зависимости между растягивающей силой и удлинением образца. Условия и порядок выполнения работы
Площадь большего поперечного сечения стержня в 2 раза превышает меньшую. Модуль продольной упругости для стали принять равнымE = 2∙105 МПа, удельный вес γ — 78 кН/м3.
Площадь приведена для меньшего поперечного стержня. Таблица 2Исходные данные к заданию 2
Задание 2. Схемы нагруженных стержней
Задание 2. (продолжение)
Задание 2 (окончание)
Пример решения задачи 2 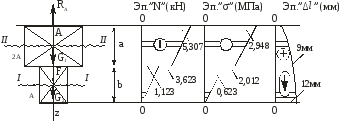 Дано:
 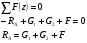 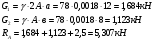
Границами участков являются сечения, в которых приложены внешние силы, и место изменения размеров поперечного сечения. Таким образом, заданный стержень имеет два участка. Применим метод сечений, оставляем нижнюю часть и «мысленно» отбрасываем верхнюю отсеченную часть стержня.
Проведем произвольное сечение на участке I-I.
Построим эпюру, показывающую как меняется, 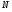 по длине стержня. Для этого, проведя ось абсцисс графика параллельно оси стержня, откладываем в произвольном масштабе значения продольных сил по оси ординат. Полученный график принято штриховать, при этом штриховка должна быть перпендикулярна оси стержня. по длине стержня. Для этого, проведя ось абсцисс графика параллельно оси стержня, откладываем в произвольном масштабе значения продольных сил по оси ординат. Полученный график принято штриховать, при этом штриховка должна быть перпендикулярна оси стержня.
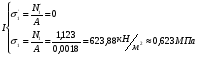 
 Эпюру перемещений следует строить от защемленного конца
 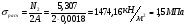  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

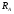 в жесткой заделке в т.А:
в жесткой заделке в т.А: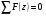 при
при 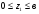
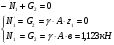
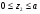
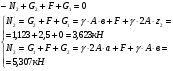
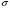 , возникающих в сечениях стержня:
, возникающих в сечениях стержня: сечений после деформации:
сечений после деформации: