курсовая. Курсовая работа кубики б. П. Никитина как средство обучения порядковому счету детей шестого года жизни
 Скачать 91.14 Kb. Скачать 91.14 Kb.
|
|
1.2 Кубики Б. П. Никитина как средство обучения порядковому счету детей шестого года жизни Обучение математике детей дошкольного возраста немыслимо без использования занимательных игр, задач, развлечений. Дети очень активные в восприятии задач – шуток, логических упражнений, головоломок. Одной из универсальных технологий является дидактический материал технологии Б. П. Никитина [17]. Этот материал можно использовать, начиная с младших групп детского сада и заканчивая школой. Развивающий дидактический материал Б. П. Никитина дает возможность для: 1) знакомства с понятиями (цвет, величина, длина, высота); 2) изучения счета и называния чисел в обратном порядке; 3) знакомства с составом числа; 4) усвоения отношений между числами, употребления знаков <,>, =; 5) измерения объектов; 6) деления целого на части; 7) овладения пространственными связями («слева», «правее», «между» и т. п.); 8) развития творческих возможностей, воображения, моделирования [23]. Игры Никитина призваны развивать у ребенка интеллектуальные и творческие способности с самых первых лет жизни. Их авторы – известные педагоги-новаторы, супруги и родители семерых детей Борис Львович и Лена Алексеевна Никитины. Этой выдающейся семье принадлежит и разработка уникальной методики раннего развития. Игры — «уникуб», «кубики для всех», «сложи квадрат» — рассчитаны на совместную игру. Они вариативные, многоуровневые. Это игры-головоломки для развития логического и образного мышления. Каждая игра — набор задач, которые ребенок решает с помощью кубиков, кирпичиков, квадратов из картона, пластика, деталей из конструктора - механика. Игры строятся в порядке возрастания сложности «от простого к сложному». Игры Никитиных напоминают блоки Фридриха Фребеля, немецкого педагога XIX века, основателя первых детских садов — KinderGarten тем, что знакомят ребенка со свойствами геометрических тел, учат его пространственному воображению, умению соединить часть в целое. Школьная методика обучения счету учит действовать по правилу, «по алгоритму», как машина, т.е. «без ума», а эти 40 задач имеют и «умные», красивые решения, находя которые задачу можно решить и быстро, и безошибочно. И тот, кто нашел быстрое решение, поумнеет сам, разовьет свои творческие способности в арифметике. «Мы советуем сделать таблицу возможно раньше и... обрадоваться, когда ваш малыш сам подойдет к ней и начнет считать, показывая на цифры: «Один, два, три, четыре!» [18]. По мнению А. В. Белошистой [2] технология Б. П. Никитина способствует развитию тонкой моторики руки, пространственного мышления и творческого воображения, умения сравнивать, анализировать, сопоставлять. В играх с совершенствуются внимание и память. Например, игра «Дроби». На трех фанерных дощечках расположены по 4 круга: одинаковые по размеру, но разные по цветам. Первый круг - целый, второй - разрезан на две равные части, третий - на три, — и так вплоть до 12. Пособие позволяет закрепить знание цветов, счета, умения сравнивать предметы. Незаменимы игры Б. П. Никитина при обучении элементов решения задач. С помощью этих игр можно еще в детском саду познакомить детей с арифметической прогрессией, своеобразной «цветной алгеброй», готовящей к изучению школьной алгебры Например, задача: «Составь 2 поезда так, чтобы водном из них было 3 розовых вагонов, а другой, состоящий тоже из розовых вагонов, был на 1 (2) вагон длиннее». Данная технология позволяет формировать умственные действия (анализ, синтез, сравнение, обобщение, классификация, аналогия) [13]. Таким образом, развивающие игры Б. П. Никитина являются элементами множества с точки зрения математики. В данном множестве «спрятаны» многие математические понятия. В процессе работы с ними у детей развивается способность сравнивать предметы по цвету, форме, величине; определять их место положения в пространстве, развивается глазомер, уточняются и закрепляются знания об основных цветах и их оттенках. Применение игр содействует успешному обучению ребёнка математике за счет осуществлении принципа наглядности, представления сложных теоретическо-математических понятий в легкодоступной для детей форме. ГЛАВА 2. ПРАКТИЧЕСКАЯ РАБОТА ПО ОБУЧЕНИЮ ПОРЯДКОВОМУ СЧЕТУ ДЕТЕЙ ШЕСТОГО ГОДА ЖИЗНИ 2.1 Диагностика уровня сформированности счетной деятельности у детей шестого года жизни Исследование проводилось в три этапа (констатирующий, формирующий, контрольный эксперименты). В процессе констатирующего этапа был выявлен начальный уровень развития и сформированности счета у старших дошкольников. На втором, формирующем этапе эксперимента было апробировано содержание работы по развитию счетной деятельности у детей старшего дошкольного возраста. На третьем, контрольном этапе эксперимента была проведена повторная диагностика уровня развития счета, проведен сравнительный анализ результатов констатирующего и контрольного этапов эксперимента. Для проведения экспериментальной работы была выбрана подготовительная группа, отобраны 12 детей с приблизительно одинаковым уровнем развития математических представлений. Таблица 1. Списочный состав детей
Изначально диагностика уровня развития детей проводилась по разделам программы математического развития: Число; Счет, число. Диагноз основывался в первую очередь на результатах наблюдений за ребенком на занятиях и в повседневной жизни, а также на диагностических методиках, предложенных А.В. Белошистой: - Подсчитайте, сколько всего кругов (5 кругов расположены в беспорядке). - Подсчитайте, сколько там квадратов (4 квадрата расположены в ряд). - Где больше цифр: где 5, или где 4? - На что можно рассчитывать в группе? Посчитай это. - А дома, на что ты можешь рассчитывать? Запомни, посчитай и скажи мне, сколько? - Возьмите круги (4) и квадраты (5). Как вы узнаете, равны ли они? Или квадратов больше, чем кругов? Какое число больше: 4 или 5? Какое число меньше: 5 или 4? - Ребенка просят сосчитать (5) маленьких кукол и (5) больших медведей. Каких предметов больше: маленьких кукол или больших медведей; Как проверить? - Ребенка просят сосчитать квадраты (4), расположенные по кругу и в линию. Где квадратов меньше: где они расположены в линию или по кругу? Как проверить? - Ребенка просят сосчитать грибы (5), расположенные близко и далеко друг от друга. Где больше грибов: где они стоят близко или далеко друг от друга? К высокому уровню развития относятся те дети, которые обладают навыками счета предметов (до 8-10), обнаруживают зависимости и взаимосвязи между числами. Обладать навыками наложения и применения объектов с целью доказательства их равенства и неравенства. Установите независимость количества объектов от их расположения в пространстве путем сравнения, подсчета объектов (на одном и том же количестве объектов). Они осмысленно отвечают на вопросы, объясняют метод сопоставления и обнаружения совпадений. Дети со средним уровнем развития обладают достаточными навыками в подсчете предметов (до 4-7), при этом используют приемы наложения и перекрытия для того, чтобы доказать равенство и неравенство. С помощью взрослого устанавливается независимость количества предметов от их расположения в пространстве. Но им трудно делать заявления и объяснения. Низкий уровень развития диагностируется у тех детей, которые допускают ошибки при подсчете предметов (до 3-5), не обнаруживают зависимостей и взаимосвязей между числами. Они плохо владеют приемами наложения и нанесения; даже с помощью взрослого трудно установить независимость количества объектов от их расположения в пространстве. Таким образом, ребенку предлагается решить ряд арифметических задач и ответить на вопросы, связанные со знанием числового материала. Таблица 2. Первый срез
В результате диагностики развития воспитанников были получены следующие показатели: Таблица 3. Анализ результатов
Представим полученные данные в процентном соотношении (Таблица 4). Таблица 4.
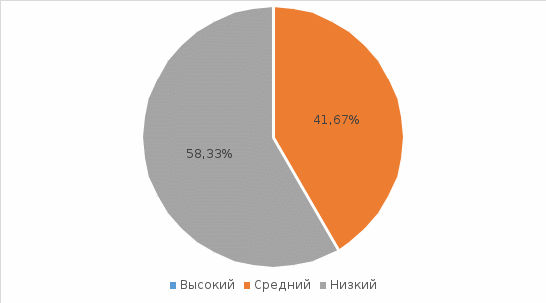 Рисунок 1. Результаты констатирующего эксперимента Таким образом, вероятность успеха составляет 33%. 4 ребенка (33%) довольно легко оперируют числовым материалом, выполняют простейшие арифметические действия. 8 детей (67%) испытывают трудности с выполнением заданий. Наблюдение показало, что дети лучше всего освоили сравнение предметов по размеру и групп предметов по количеству. Наиболее успешно справляются со сравнением множеств, со сравнением элементов одного множества с элементами другого, различают равенство и неравенство групп объектов, составляющих множество. Трудности в большинстве предметов вызваны навыками устного счета и знакомством с цифрами. Концепция появления каждого нового числа путем добавления единицы плохо сформирована. Дети также показали низкий уровень развития при овладении такими приемами, как сравнение двух чисел, сравнение, установление равенства и неравенства между ними. Почти все дошкольники испытывают трудности с умением отличать порядковый счет от количественного, хотя большинство детей справились с порядковым счетом. Таким образом, на констатирующем этапе эксперимента были выявлены самые слабые показатели уровня математического развития во всем разделе и в отдельных его частях. 2.2 Использование Кубиков Б. П. Никитина при обучении порядковому сету детей шестого года жизни При обучении математике дошкольников дидактический материал Б. П. Никитина рассматривается с использованием математических представлений. Формирование количественных представлений, умение различать количественный и порядковый счет, устанавливать равенство и неравенство двух групп испытуемых. Для развития математических способностей дошкольников использовались следующие развивающие игры: игры Б. П. Никитина "Сложи узор", "Сложи квадрат", "Уникуб", "Кубики для всех". Формирование представлений о составе числа из единиц и из двух меньших. Знакомство с образованием чисел в пределах 10 и на основе измерения и цвета. Формирование у детей умения различать количественный и порядковый счет, отвечать на вопросы: «Какой? Сколько?» Закреплять умения делить целое на равные части, умения измерять с помощью условной мерки. Использование чисел в цвете помогали развивать у детей представление о числе на основе счета и измерения. Выделение цвета и длины помогали дошкольникам освоить ключевые для их возраста средства познания - сенсорные эталоны, эталон цвета, размера, и такие способы познания, как сравнение, соотношение предметов по цвету, ширине, длине, высоте. От элементарной игры с цветными кубиками дети постепенно переходили к пониманию пространственных и количественных характеристик. Например, развивающая игра «Сложи узор». Комплект состоит из 16 деревянных кубиков одинакового размера, уложенных в коробку. Грани кубиков окрашены по-разному в 4 цвета, что позволяло составлять из них множество вариантов цветных узоров. К игре прилагаются два блокнота с образцами - заданиями: из 4-х кубиков (серия А, из 9-ти кубиков (серия В) и из 16-ти кубиков (серии С, D). Задания даны с постепенным усложнением. Начинать игру можно индивидуально с детьми, на основе подражания. Материал. Карточка; набор счетных палочек. Например, далее мы рассматривали кубики. Разложили их по «сортам». Распределили по числу граней какого - либо из цветов. Например, если по красному цвету - то выделяются кубики с одной, 2-мя, 3-мя красными гранями по кучкам. Использование«чисел в цвете» позволяли развивать у дошкольников представление о числе на основе счета и измерение. Например, варианты игры: 1. Складывание площадки из 9-ти кубиков. 2. Складывание площадки из 16-ти кубиков. Усложнение работы с игрой «Уникуб» 1. Учить складывать малый куб из 4-х кубиков синего (красного цветов). 2. Учить складывать малый куб из 8-и кубиков синего (красного цветов). Формируя элементарные математические представления у дошкольников средствами игр Б.П. Никитина, мы убедились в том, что, играя в них, ребенок выступает как активная сторона и у него воспитывается не умение выполнять работу по предложенному шаблону, а развивается логическое и образное мышление, творчество, умение распознать. Используя развивающие игры в работе с дошкольниками, мы видели их интерес к познавательной деятельности, и постепенное развитие, как математических способностей, так и развитие интеллектуальных способностей в целом. Дети с удовольствием играли в игры, мы давали возможность использовать их в самостоятельной деятельности. 2.3 Сравнение результатов исследования Для проверки, проделанной нами работы на этапе формирования эксперимента был проведен контрольный эксперимент. С целью выявления эффективности работы, проделанной на формирующем этапе эксперимента, мы провели повторную диагностику проверки уровня математических способностей у детей 6 лет. Детям также было предложено решить ряд арифметических задач и ответить на вопросы, связанные со знанием числового материала. Таблица 5. Второй срез.
В результате диагностики развития воспитанников были получены следующие показатели: Таблица 6. Анализ результатов
Представим данные в процентном соотношении (Таблица 7).
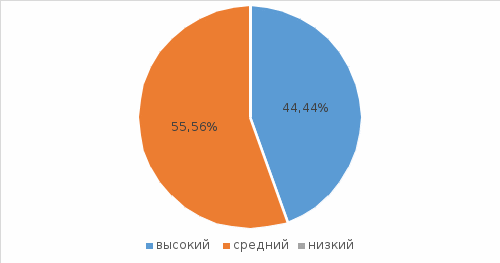 Рисунок 2. Результат формирующего эксперимента Таким образом, успешность составлил 100 %. 12 детей (100%) достаточно легко оперируют числовым материалом, выполняют простейшие арифметические операции. Дошкольники стали лучше владеть навыками счета, сравнением двух множеств, выраженных смежными числами. У дошкольников сформировались понятия о порядковом и количественном счете, ими освоены такие приемы, как сравнение двух чисел, сопоставление, установление равенства и неравенства их, счет по осязанию, счет на слух и счет различных движений в пределах 10. Дети лучше овладели приемом отсчитывания предметов из большего количества, а также усвоили значение порядковых числительных. Таким образом, в результате теоретического изучения данного вопроса и проведенной практической экспериментальной работы можно сделать вывод о том, что применение эффективных приемов обучения детей счету (на примере подготовительной группы), позволяет заметно улучшить качество и продуктивность данной работы. Что подтверждает заявленную нами в начале работы гипотезу. А это, в свою очередь, приводит к значительному росту показателей уровня развития счетной деятельности у детей дошкольного возраста, а также к интеллектуально – познавательному развитию в целом и формированию общей готовности к школе. Мы знаем, что математика - это мощный фактор интеллектуального развития ребенка, формирования его познавательных и творческих способностей. Таким образом, на основании предоставленного опыта можно сделать вывод о том, что в игровой форме ребенок лучше усваивает знания из области математики. В процессе игры дети усваивают сложные математические понятия, учатся считать и писать, развиваются память, мышление, творческие способности. Заключение Счет – это первая и основная математическая деятельность, основанная на поэлементном сравнении конечных множеств. Счетная деятельность – деятельность по вычислению, определению каких-либо количественных показателей или перечисление элементов последовательности чисел. Под влиянием овладения счетом у детей дошкольного возраста формируются четкие представления о месте, порядке следования, количественном значении числа, отношении его к другим числам (в пределах 10). Важно то, что овладения знаниями о числе и счете позволяет детям перейти к новому виду деятельности – арифметическим вычислениям. Развивающие игры Б. П. Никитина являются элементами множества с точки зрения математики. В данном множестве «спрятаны» многие математические понятия. В процессе работы с ними у детей развивается способность сравнивать предметы по цвету, форме, величине; определять их место положения в пространстве, развивается глазомер, уточняются и закрепляются знания об основных цветах и их оттенках. Применение игр содействует успешному обучению ребёнка математике за счет осуществлении принципа наглядности, представления сложных теоретическо-математических понятий в легкодоступной для детей форме. В данной работе были проведена исследовательская работа. Работа носила констатирующий, формирующий, контрольный этап. Проведение исследования показала нам, что результаты констатирующего и контрольного этапов заметно изменились. Так как в формирующем этапе, нами была проведена работа с использованием кубиков Б. П. Никитина. У дошкольников сформировались понятия о порядковом и количественном счете, ими освоены такие приемы, как сравнение двух чисел, сопоставление, установление равенства и неравенства их, счет по осязанию, счет на слух и счет различных движений в пределах 10. Дети лучше овладели приемом отсчитывания предметов из большего количества, а также усвоили значение порядковых числительных. Формируя элементарные математические представления у дошкольников средствами игр Б.П. Никитина, мы убедились в том, что, играя в них, ребенок выступает как активная сторона и у него воспитывается не умение выполнять работу по предложенному шаблону, а развивается логическое и образное мышление, творчество, Необходимо отметить, что регулярное использование на занятиях по математике игровых систем с использованием кубиков Б. П. Никитина, направленных, расширение математического кругозора дошкольников возраста 6 лет, способствует математическому развитию, повышает качество математической подготовленности к школе, позволяет детям более уверенно ориентироваться в простейших закономерностях цифр и активнее использовать математические знания в повседневной жизни. Список литературы Безруких М.М. Чему и как учить до школы // Дошкольное воспитание, 2016. №3. С.62 - 65. Белошистая А.В. К вопросу о развитии счетных навыков у дошкольников /А.В. Белошистая // Дошкольное воспитание. 2010. №4. С. 8-12 Блехер Ф. Развитие первоначальных математических представления у детей дошкольного возраста // Дошкольное воспитание. 2008. - № 11. - С. 14-23. Богданова Е.А. Формирование счетной деятельности у дошкольников /Е.А. Богданова // Дошкольное воспитание, 2014. №10. С. 21-26. Волкова С.И. Изучение курса «Математика» в ДОУ // Дошкольное воспитание, 2012. №9-10. С. 22-31. Дейнга Л. В. "Удивительные кубики Б.П.Никитина" https://videouroki.net/razrabotki/udivitiel-nyie-kubiki-b-p-nikitina.html (дата обращения 25.03.2022) Ерофеева Т. И. Знакомство с математикой / Т. И. Ерофеева. – М.: Просвещение, 2014. 112 с. Ерофеева Т. Планирование занятий по математике // Ребенок в детском саду, 2003. № 4. с. Есмурзаева В. Б. Дидактические игры в развитии математических способностей старших дошкольников//Воспитатель дошкольного образовательного учреждения, 2019. № 1. с. 54-57. Колесникова Е. В. Я считаю до двадцати. Математика для детей 6-7 лет / Е. В. Колесникова. М.: Гном-Пресс, 2013. 96 с Котельникова С. Н. Методический сборник на тему: «Развивающие игры Б.П. Никитина как средство формирования математических представлений» https://www.prodlenka.org/metodicheskie-razrabotki/472176-metodicheskij-sbornik-na-temu-razvivajuschie-(дата обращения 25.03.2022) Леушина А. М. Формирование элементарных математических представлений у детей дошкольного возраста / А. М. Леушина. – М.: Детство-Пресс, 2007. 193 с. Макурин, А. А. Опыт и педагогическое наследие семьи Никитиных: подготовка к школьному образованию и диалог со школой / А. А. Макурин // На пути в педагогическую науку : сборник докладов студенческой научной конференции ВлГУ, Владимир, 30 марта 2017 года / ФГБОУ ВО "Владимирский государственный университет имени А.Г. и Н.Г .Столетовых". Владимир: Шерлок-пресс, 2017. С. 139-145. Микляева Н., Микляева Ю. Теория и технологии развития математических представлений у детей / Н. Микляева. - М.: Академия, 2016. Никитин Б. П.Интеллектуальные игры. Изд. 6-е, испр. и доп. Обнинск, “Световид”, 2009. 216 с. Никитин, Б.П. Ступеньки творчества или развивающие игры / Б.П. Никитин. М.: Просвещение, 1991. 120 с. Обучение математике по методу Никитиных https://kladraz.ru/podgotovka-k-shkole/obuchenie-matematike-po-metodu-nikitinyh.html (дата обращения 28.03.2022) Овчинникова Е. О совершенствовании элементарных математических представлений // Дошкольное воспитание, 2005. № 8. с. 42-54. От рождения до школы: основная общеобразовательная программа дошкольного образования / под ред. Н. Н. Вераксы, Т. С. Комаровой, М. А. Васильевой, В. В. Гербовой. М.: Мозаика-Синтез, 2016. – 412 с. Подопригора Л. С. Формирование у детей знаний о числе, счетной и вычислительной деятельности. https://nsportal.ru/detskiy-sad/matematika/2016/01/16/formirovanie-u-detey-znaniy-o-chisle-schetnoy-i-vychislitelnoy(дата обращения 20.03.2022) Сушкова И. В. Образовательные ситуации в обучении счету детейдошкольного возраста / И. В. Сушкова // Дошкольное воспитание, 2022. № 3. С. 17-23. Сушкова И.В. Об инструментальных аспектах обучения детей счету в дошкольных образовательных организациях // Дошкольное воспитание. 2017. № 9. С. 21-29. Сюжетные дидактические игры в развитии математических способностей дошкольников / И. Р. Пономаренко, С. Р. Манучарян // Воспитатель ДОУ, 2017. № 4. с. 50-53. Турбина О.И. Развитие логического мышления в процессе формирования элементарных математических представлений [Текст] / О.И. Турбина // Воспитатель ДОУ, 2016. №1. с.72-77. Щеглова А.А. Игра как средство освоения порядкового счета детьми старшего дошкольного возраста // А.А. Щеглова, Л.И. Павлова // Наука и общество в современных условиях, 2016. № 1 (4). – с. 36-40. Щербакова Е. И. Методика обучения математике в детском саду / Е. И. Щербакова. М.: Детство-Пресс, 2012. 150 с. Приложение 1. Конспект открытого занятия по математике с использованием кубиков Никитина «В поисках клада» (старшая группа) Цели и задачи: - закрепить знание детей об образовании числа 9 с использованием кубиков Никитина «Сложи узор»; - закрепить знание детей в расстановке шахматных фигур; - формировать умение сравнивать рядом стоящие цифры в пределах 10; - развивать умение составлять целое изображение предмета из его частей; - воспитывать умение работать в парах, слушать и слышать других. Методические приемы: Игровой прием – использование сюрпризных моментов; Наглядный метод – использование схем. Материалы: план – схема группы, спальни, коробка-посылка, Кубики Никитина, сундучок, шоколадные монеты, числовой отрезок, шахматы. Ход занятия: 1. Психологический настрой детей к общению Приветствие: Ребята я предлагаю встать все в круг. Собрались все дети в круг, Я твой друг и ты мой друг, Крепко за руки возьмёмся И друг другу улыбнёмся. Посмотрите друг на друга и улыбнитесь, улыбнитесь нашим гостям. Ведь от ваших улыбок всем стало тепло и приятно 1.1. Организационный момент. Воспитатель: «Сегодня рано утром, когда вас ещё не было в детском саду, я обнаружила вот эту коробку. Помогите мне её поставить на ковёр. Я ждала, когда вы прейдете, что бы вместе с вами посмотрели что в ней. Откроем коробку? (Дети открывают коробку, все, что в ней находится, выкладывают на ковёр). В: Что тут? Вы ребята понимаете, что всё это может означать и что с этим нам делать? Д: Письмо. В: Разрешите мне прочитать это письмо. 2. Введение в тему. Здесь написано: «Дорогие, ребята! Меня зовут Магнолик. Я Великий волшебник. Приглашаю к себе в Заколдованное королевство. Наверняка, вы, как и все дети, любите играть и искать клады. В моём королевстве спрятан клад, я предлагаю вам его найти. Но будьте внимательны: по дороге вас ждут испытания. Если вы их выполните, то получите частичку карты, которая непременно приведёт вас к кладу. Чтобы вы не заблудились в моём Заколдованном королевстве, посылаю вам путеводитель и чудо кубики, которые помогут вам преодолеть препятствия». В: И что нам делать? Д: Будем искать клад. 3. Основная часть. В: А про какой же нам путеводитель пишет волшебник, и где он? Посмотрите, может быть, что- то в конверте ещё осталось. Да, вот и ещё что-то. Ребята вы понимаете что это? Какие- то здесь квадратики, стрелочки. Как, вообще обращаться с этим путеводителем. Дети: Здесь задания, а стрелочки-это направление как мы должны двигаться В: Что бы узнать с чего нам начать давайте посмотрим в наш путеводитель. Дети: Начнём с первого квадратика, что же тут написано. В: Можно я прочитаю: «Цифра 6 перевернулась новой цифрой обернулась». Какой новой цифрой перевернулась цифра 6? Д: Цифрой 9. В: Ну что идём искать цифру 9. (находят, с обратной стороны цифры задание) В: Послушайте задание.» Из чудо-кубиков сложи узор используя столько кубиков, сколько указано в загадке. Для этого ты можешь воспользоваться любой предложенной схемой. В: Возьмите мешочки с кубиками, достаньте все кубики и посчитайте, сколько их у вас всего. (по 9). В: Соответствует ли число кубиков в вашем мешке цифре 9? В: Хватит вам кубиков, чтобы сложить такие узоры? Дети по схеме выкладывают узор из 9 кубиков «Сложи узор». В: - Все справились с заданием? - Проверим у всех правильно выполнены узоры? - Поменяйтесь местами и проверти. - Маша ты у кого будешь проверять? - А, ты Артур? В: А вот и первый кусочек карты появился. Значит, мы идём по верному пути. В: Смотрим в путеводитель, что у нас дальше «Эта циферка с секретом, и зимой и жарким летом Различишь едва, едва, где в ней ноги, голова» В: Какую цифру идём искать? Д: 8. В: Нашли цифру 8 (в раздевалке). Для вас есть послание от волшебника Магнолика (читаем на обратной стороне цифры 8): «Ребята этот волшебный числовой отрезок поможет вам добраться до клада, если вы правильно выполните задание». В: Давайте сосчитаем, сколько здесь всего чисел. -Надень синюю резинку на отрезок от 0 до 8; -Надень красную резинку на отрезок от 0 до 9; (что можно сказать про число 8 и 9) -Найди число, которое больше числа 3 на 1? -Найди число, которое больше числа 5 на 1 ? -Какое число меньше 6 на 1? -Какое число меньше 4 на 1? -Какое число больше числа 8 на 1 Дети выполняют на числовом отрезке задания В: Ребята как вы считаете мы справились с заданием? Воспитатель убирает с квадратика задание и появляется цифра 8. В: Смотрим в путеводитель двигаемся по направлению стрелочки, к следующему испытанию. Читаем: «Нолик стань за единицей, за своей родной сестрицей Только так, когда вы вместе, называют цифрой 10 В: Какую цифру идём искать? Д: 10 (Цифру 10 нашли перед лестницей на стене у подоконника) Снимаем цифру читаю загадку: «На квадратиках доски Короли свели полки. Нет для боя у полков Ни патронов, ни штыков». Д: Шахматы В: Верно шахматы. «Дорогие ребята! Разделитесь на пары и правильно расставьте шахматные фигуры на шахматной доске. (Дети расставляют фигуры) -Проверьте правильно вы расставили фигуры? (Взаимопроверка) - Назовите фигуры шахматные; - На какой по счёту клетке стоит король; - На какой по счёту клетке стоит ладья; - На какой по счёту клетке стоит слон; - Как ходит пешка? - Проведите пешку до стороны противника. В: У кого быстрее получилось? В: А вот и ещё часть карты появилась. (Заходят в группу, раскладывают части карты, соединяют её) В: И что это за план? Что-то я не могу понять. Д: План группы. В: А где мы сейчас с вами находимся, в каком месте? В: куда теперь нам нужно идти? Д: В спальню. В: А как нам найти клад в спальне. Д: Он обозначен стрелочкой. Идут в спальню находят кровать указанную на плане «КЛАД» (шоколадные монеты). Итог: - Что для вас было интересным в нашем путешествии? - Какие препятствия вам пришлось пройти, что бы найти клад? - Что в путешествии было сложным для вас? Я благодарю вас всех за участие в этом увлекательном путешествии. Приложение 2. Конспект открытого занятия по ФЭМП с использованием кубиков Никитина «Путешествие в страну профессий» (старшая группа) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
