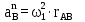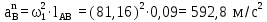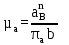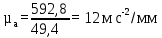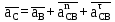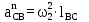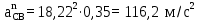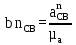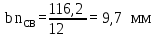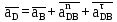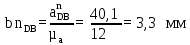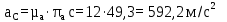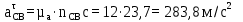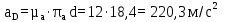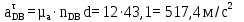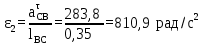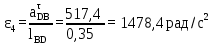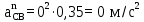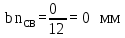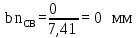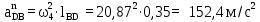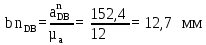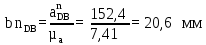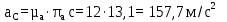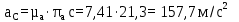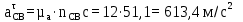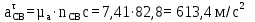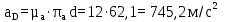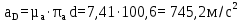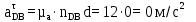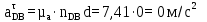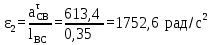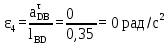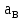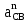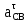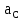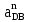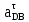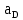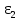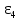ТММ курсовая. вариант12 курсовая. Курсовая работа (курсовой проект) по учебному курсу Теория механизмов и машин Вариант 12 Студент
 Скачать 0.62 Mb. Скачать 0.62 Mb.
|
Описание построения плана ускоренийНормальное (центростремительное) ускорение точки B кривошипа найдем по формуле:
где 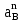 – нормальное ускорение точки B относительно точки A; – нормальное ускорение точки B относительно точки A;ω1 – угловая скорость звена 1, рад/с; rAB – длина кривошипа по заданию, м.
Рассчитаем масштабный коэффициент плана ускорений по формуле:
где µa - масштабный коэффициент ускорения, м∙с-2/мм; 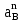 – нормальное ускорение точки B, м/с2; – нормальное ускорение точки B, м/с2;pab – длина вектора pab на плане ускорений, мм.
Изображаем на плане ускорения вектор ускорения точки B длиной 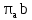 =49,4 мм направленный вдоль звена AB к центру вращения, т.е. к точке A. =49,4 мм направленный вдоль звена AB к центру вращения, т.е. к точке A.Для нахождения ускорения точки C составляем векторное уравнение:
где 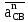 и и 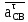 – нормальное и касательное ускорения точки C при плоско-параллельном движении звена 2. Вектор – нормальное и касательное ускорения точки C при плоско-параллельном движении звена 2. Вектор 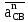 направлен вдоль звена BC от точки C к точке B, вектор направлен вдоль звена BC от точки C к точке B, вектор 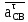 направлен перпендикулярно звену BC. направлен перпендикулярно звену BC.Определяем нормальное ускорение 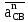 по формуле: по формуле:
где 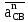 - вектор нормального ускорения точки C относительно B; - вектор нормального ускорения точки C относительно B;ω2 – угловая скорость шатуна BC, рад/с; lBC – действительная длина шатуна BC, м.
Определим длину вектор bnCB, изображающего на плане нормальное ускорение 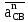 : :
где bnCB – длина вектора нормального ускорения точки B, мм; 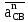 - вектор нормального ускорения точки C относительно B; - вектор нормального ускорения точки C относительно B;µa - масштабный коэффициент ускорения, м∙с-2/мм;
Векторное уравнение (19) решаем графически. Для нахождения ускорения точки D составляем векторное уравнение:
где 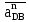 и и 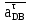 - нормальное и касательное ускорения точки D при плоско-параллельном движении звена 4. Вектор - нормальное и касательное ускорения точки D при плоско-параллельном движении звена 4. Вектор 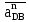 направлен вдоль звена BD от точки D к точке B, вектор направлен вдоль звена BD от точки D к точке B, вектор 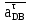 направлен перпендикулярно звену BD. направлен перпендикулярно звену BD.Определяем нормальное ускорение 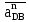 по формуле (20): по формуле (20):
Определим длину вектор bnDB, изображающего на плане нормальное ускорение 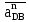 : :
Векторное уравнение (22) решаем графически. Измеряем на чертеже размеры отрезков 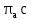 и и 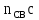 , , 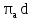 и и 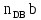 и определяем соответствующие ускорения: и определяем соответствующие ускорения:
Определим угловое ускорение звена 2 и 4:
Для «0-го» положения:
Значения ускорений всех точек механизма и угловых ускорений звеньев сводим в таблицу Табл. 5. Табл. 5 - Значения линейных и угловых ускорений
План ускорений для 10-го положения представлен на Рис. 9 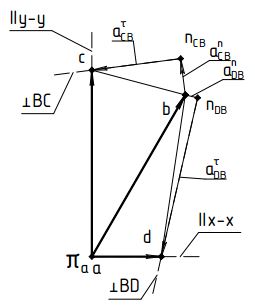 Рис. 9 План ускорений положение 10 План ускорений для 0-го положения представлен на Рис. 9 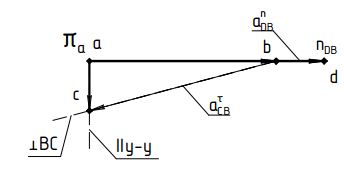 Рис. 10 План ускорений положение 0 |