ТММ курсовая. вариант12 курсовая. Курсовая работа (курсовой проект) по учебному курсу Теория механизмов и машин Вариант 12 Студент
 Скачать 0.62 Mb. Скачать 0.62 Mb.
|
Сравнительный анализСравним результаты для 0 и 10 положений механизма. 1) 0 положение механизма:
Относительная погрешность составляет:
Сравним величины ускорений:
Относительная погрешность составляет:
2) 10 положение механима:
Относительная погрешность составляет:
Сравним величины ускорений:
Относительная погрешность составляет:
Результаты сравнительного анализа сводим в Табл. 6 Табл. 6 – Результаты сравнительного анализа
Тема 2. Синтез кулачкового механизмаИсходные данные и схема механизмаДля проектирования кулачкового механизма нам заданы следующие параметры: фаза удаления φу=1040, фаза дальнего стояния φдс=220, фаза возвращения φв=1040, максимальный ход толкателя hmax=38 мм, минимально допустимый угол передачи движения γmin=450. Схема кулачкового механизма представлена на Рис. 11 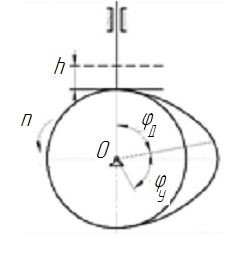 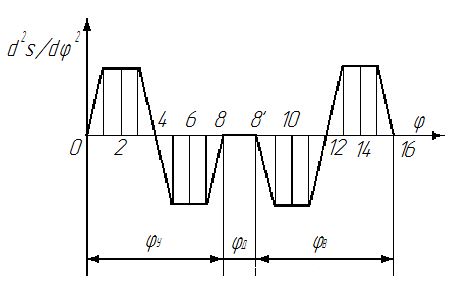 Рис. 11 Схема кулачкового механизма Построение диаграммы аналога ускоренийВ произвольном масштабе вычерчиваем заданную диаграмму аналогов ускорений толкателя в функции угла поворота кулачка 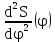 . Рабочая фаза кулачка φраб: . Рабочая фаза кулачка φраб: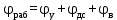 Получаем: 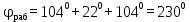 Масштабный коэффициент графиков по оси φ: 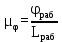 где Lраб – длина рабочей фазы кулачка на графике (принимаем равным 230 мм). 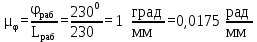 Переводим углы в радиальные значения: 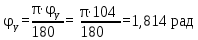 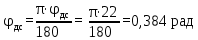 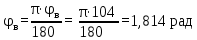 Определим длину отрезков на диаграмме, соответствующих углам 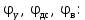 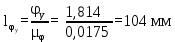 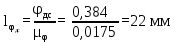 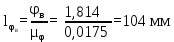 За величину амплитуды на положительном участке фазы удаления принимаем равной у=38 мм. Тогда, на фазе возврата величину амплитуды определим по формуле: 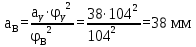 Плечо интегрирования ОР вычислим по следующей формуле:
где OP – длина отрезка OP на чертеже, мм; Построив заданную диаграмму аналога ускорений толкателя в зависимости от угла поворота кулачка 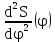 и графически проинтегрировав ее, получаем графики аналога скорости и графически проинтегрировав ее, получаем графики аналога скорости 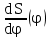 толкателя. толкателя.Фазы удаления и приближения диаграммы 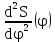 разбиваем по оси на 14 участков (0-1; 1-2; 2-3; и т. д.). Слева от начала координат на расстоянии 57,14 мм ставим точку Р. Соединим эту точку с точками 1", 2", 3" и т.д. ступенчатой диаграммы лежащими на оси ординат, получим лучи р - 1", р - 2"; р - 3"; и т.д. разбиваем по оси на 14 участков (0-1; 1-2; 2-3; и т. д.). Слева от начала координат на расстоянии 57,14 мм ставим точку Р. Соединим эту точку с точками 1", 2", 3" и т.д. ступенчатой диаграммы лежащими на оси ординат, получим лучи р - 1", р - 2"; р - 3"; и т.д.Над диаграммой 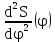 проводим оси координат диаграммы проводим оси координат диаграммы 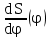 и разбиваем ось на участки, равные соответствующим участкам диаграммы и разбиваем ось на участки, равные соответствующим участкам диаграммы 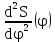 . Далее на участке 0-1 проводим из начала координат отрезок 0-1’, параллельный лучу р-1", из полученной точки 1’ на участке 1-2 проводим отрезок 1’-2' параллельный р - 2"; из точки 2' проводим отрезок 2’-3’, параллельный лучу р - 3" и т.д. Полученная ломаная линия представляет собой диаграмму . Далее на участке 0-1 проводим из начала координат отрезок 0-1’, параллельный лучу р-1", из полученной точки 1’ на участке 1-2 проводим отрезок 1’-2' параллельный р - 2"; из точки 2' проводим отрезок 2’-3’, параллельный лучу р - 3" и т.д. Полученная ломаная линия представляет собой диаграмму 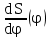 (аналога скорости толкателя в функции угла поворота кулачка). Затем еще раз графически интегрируем, выбрав полюсное расстояние OP таким же 57,14 мм. Полученная кривая зависимость перемещения толкателя от угла поворота кулачка (аналога скорости толкателя в функции угла поворота кулачка). Затем еще раз графически интегрируем, выбрав полюсное расстояние OP таким же 57,14 мм. Полученная кривая зависимость перемещения толкателя от угла поворота кулачка 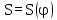 . .Отрезок Smax на графике S(φ) получился равным Smax= 22,05 мм. Теперь можно определить масштабы графиков 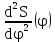 , , 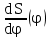 и S(φ): и S(φ): 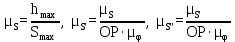 где hmax – максимальный ход толкателя (по заданию 38 мм); OP – плечо интегрирования на чертеже (равно 57,14 мм); Таким образом: 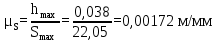 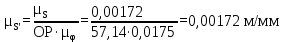 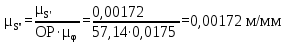 Определение минимального радиуса кулачкаБерем на плоскости произвольную т. A, откладываем от неё отрезок АB, равный ходу h толкателя. Этот отрезок размечаем в соответствии с диаграммой 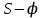 . Через точки деления проводим перпендикуляры к линии АB. От точек деления на перпендикулярах откладываем отрезки, взятые из графика . Через точки деления проводим перпендикуляры к линии АB. От точек деления на перпендикулярах откладываем отрезки, взятые из графика 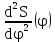 . Эти отрезки нужно откладывать в том масштабе, в котором отложен отрезок АB, т.е. в масштабе . Эти отрезки нужно откладывать в том масштабе, в котором отложен отрезок АB, т.е. в масштабе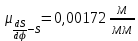 . Соединяем плавной кривой концы этих отрезков и получаем кривую . Соединяем плавной кривой концы этих отрезков и получаем кривую 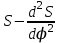 . К полученной кривой проведем касательные под углом γmin =450 к крайним точкам кривой. Из области, ограниченной этими лучами определяется зона возможного положения центра кулачка. Принимаем длину отрезка АО равной r0= 40 мм на чертеже. Следовательно, минимальный теоретический радиус кулачка будет равен: . К полученной кривой проведем касательные под углом γmin =450 к крайним точкам кривой. Из области, ограниченной этими лучами определяется зона возможного положения центра кулачка. Принимаем длину отрезка АО равной r0= 40 мм на чертеже. Следовательно, минимальный теоретический радиус кулачка будет равен: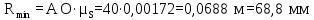 где Rmin– минимальный теоретический радиус кулачка, м; μS– масштабный коэффициент, м/мм; r0– минимальный радиус кулачка на чертеже, мм. Профилирование кулачка методом обращенного движения.Профилирование кулачка проводим методом обращения движения, который заключается в следующем: мысленно придаем всему механизму вращение вокруг центра вращения кулачка с угловой скоростью ( 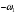 ), равной по величине, но противоположной по направлению угловой скорости кулачка. Тогда угловая скорость кулачка станет равной нулю, т.е. кулачок как бы остановится. ), равной по величине, но противоположной по направлению угловой скорости кулачка. Тогда угловая скорость кулачка станет равной нулю, т.е. кулачок как бы остановится.Толкатель, помимо своего абсолютного движения, получит добавочное движение - вращение вокруг оси кулачка с угловой скоростью ( 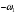 ). ).При этом относительное положение толкателя и кулачка не нарушится, и при любых произвольно выбранных положениях тарелка всегда касается профиля шайбы; вследствие чего расстояние от центра тарелки до центра вращения кулачка в обращенном движении равным тому же расстоянию, что и при прямом ходе. Всему механизму (толкателю, стойке) условно сообщаем вращение вокруг центра вращения кулачка с угловой скоростью, равной угловой скорости кулачка, но противоположно направленной. Зададимся масштабом построения: 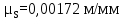 Проведём окружность радиусом r0 равным 40 мм. В произвольном месте окружности выберем точку отсчета – т. В0. Соединим точку В0 с точкой О. От полученного луча в направлении (–ω) отложим угол φу, получим точку 14. Дугу В014 разделим на 14 равных частей (получим точки 1, 2, 3, …). Откладываем окружности, соответствующие перемещению толкателя в каждом из положений. Отмечаем точки пересечения отрезков О1, О2,… с соответствующими окружностями и получаем точки B1, B2, … B12. Полученные точки соединяют плавной кривой – это теоретический профиль кулачка. Построив все положения тарелки толкателя, строим огибающую к тарелкам, которая и является искомым профилем кулачка. Список использованной литературы1. Артоболевский, И.И. Теория механизмов и машин. / И.И. Артоболевский. - М.: Альянс, 2016. - 640 c. 2. Коловский, М.З. Теория механизмов и машин / М.З. Коловский, А.Н. Евграфов и др. - М.: Academia, 2015. - 192 c. 3. Кудинов, Ю.И. Теория механизмов и машин. Учебно-метод. пос. КПТ Ю.И. Кудинов, Ф.Ф. Пащенко. - СПб.: Лань КПТ, 2016. - 288 c. |

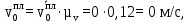
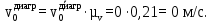
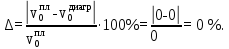
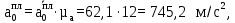
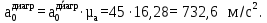
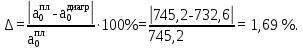
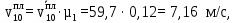
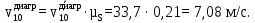
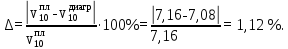
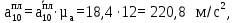
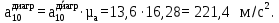
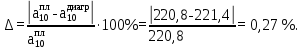
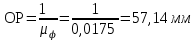 ,
,