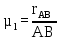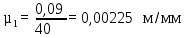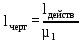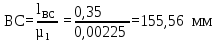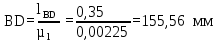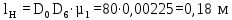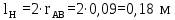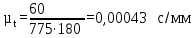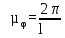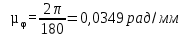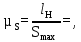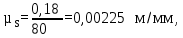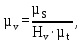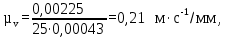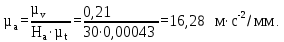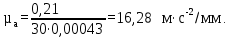ТММ курсовая. вариант12 курсовая. Курсовая работа (курсовой проект) по учебному курсу Теория механизмов и машин Вариант 12 Студент
 Скачать 0.62 Mb. Скачать 0.62 Mb.
|
Описание построения плана механизмаРасчет масштабного коэффициента производим по формуле:
где µl - масштабный коэффициент, м/мм; rAB – длина кривошипа по заданию, м; AB – длина кривошипа на чертеже, мм. Примем длину кривошипа на чертеже AB=40 мм. Тогда масштаб:
Расчет длин звеньев механизма на чертеже ведем, используя следующую формулу:
где lчерт – длина звена на чертеже, мм; lдейств – действительная длина звена, м; µl – масштабный коэффициент, м/мм.
Сначала изображаем неподвижную опору A, неподвижные направляющие и начальное положение звена AB. За начальное положение кривошипа принимаем крайнее левое положение звена 5. Поворачиваем кривошип на 3600 по ходу его вращения с шагом 300. Получаем 12 положений точки B и траекторию ее движения – окружность. С помощью метода засечек определяем положение точек C и D для каждого из 12-ти положений кривошипа и строим 12 положений шатунов BC и BD. Выделяем на плане положение φ=600 толстыми линиями согласно варианту задания. Измеряем на плане положений расстояние между крайними точками D0 и D6, определяем ход ползуна D:
где D0D6 – расстояние между крайними точки D0 и D6, мм. Проверяем полученное графически значение хода ползуна по следующей формуле:
Значения совпадают, значит построения выполнены верно. План механизма представле на Рис. 3. 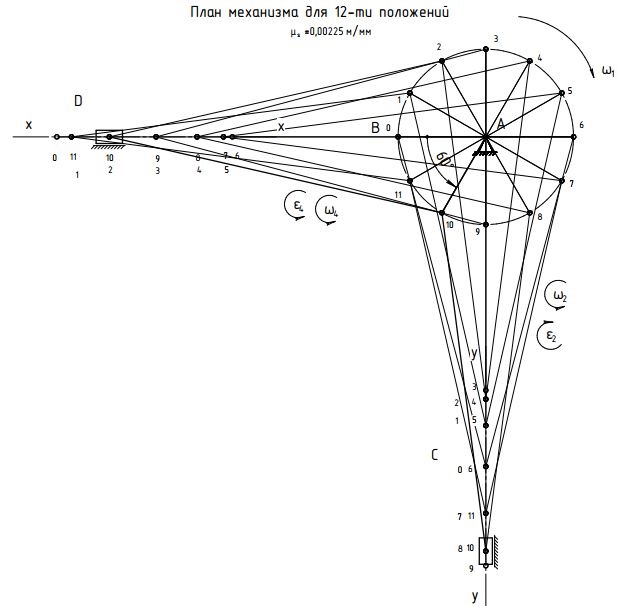 Рис. 3 План механизма Построение кинематических диаграммПостроим кинематические диаграммы перемещения 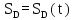 , диаграмму скорости , диаграмму скорости 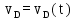 и ускорения и ускорения 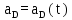 для движения точки D механизма. для движения точки D механизма.Проводим две оси координат и на оси абсцисс откладываем отрезок l, представляющий собой в масштабе 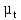 время Т одного полного оборота кривошипа: время Т одного полного оборота кривошипа:
где 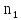 – частота вращения кривошипа, об/мин – частота вращения кривошипа, об/минl - длина отрезка оси абсцисс, мм, µt – масштабный коэффициент времени на диаграмме, с/мм. Принимаем l=180 мм. Масштаб 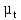 времени будет равен: времени будет равен:
Масштабный коэффициент угла поворота кривошипа найдем по формуле:
где µφ – масштабный коэффициент угла поворота кривошипа, рад/мм; l - длина отрезка оси абсцисс (приняли l=180 мм). Тогда масштаб:
Отрезок l разбиваем на 12 равных частей и в соответствующих точках 1,2,3, … откладываем расстояния, пройденные точкой D от крайнего положения 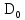 звена 5. Так, в точке 1, откладываем в направлении, параллельном оси ординат, отрезок звена 5. Так, в точке 1, откладываем в направлении, параллельном оси ординат, отрезок 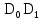 , в точке 2 – отрезок , в точке 2 – отрезок 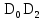 и т.д. Таким образом, кривая и т.д. Таким образом, кривая 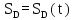 в положении, когда кривошип 1 придет в начальное положение, будет иметь ординату, равную нулю. Полученная кривая является кривой перемещения точки D от крайнего положения звена 5. в положении, когда кривошип 1 придет в начальное положение, будет иметь ординату, равную нулю. Полученная кривая является кривой перемещения точки D от крайнего положения звена 5.Далее строим диаграмму скорости 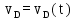 методом хорд. Заменим на всех участках дуги хордами. Строим координатные оси и по оси абсцисс влево откладываем произвольный отрезо методом хорд. Заменим на всех участках дуги хордами. Строим координатные оси и по оси абсцисс влево откладываем произвольный отрезо 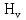 , затем из конца этого отрезка проводим лучи, параллельные хордам до пересечения с ось ординат диаграммы скоростей. Точки диаграммы скоростей найдутся на пересечении прямых, проходящих через точки пересечения лучей с осью ординат диаграммы скоростей и параллельных оси , затем из конца этого отрезка проводим лучи, параллельные хордам до пересечения с ось ординат диаграммы скоростей. Точки диаграммы скоростей найдутся на пересечении прямых, проходящих через точки пересечения лучей с осью ординат диаграммы скоростей и параллельных оси 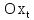 с соответствующими прямыми, параллельными оси с соответствующими прямыми, параллельными оси 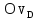 и проведенными через середины отрезков 0-1, 1-2, 2-3, 3-4. Диаграмма ускорений и проведенными через середины отрезков 0-1, 1-2, 2-3, 3-4. Диаграмма ускорений 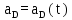 строится аналогичным образом. Опредим масштабы графиков по формулам: строится аналогичным образом. Опредим масштабы графиков по формулам:
где lH – вычисленный ранее ход ползуна D, м; Smax – максимальная ордината на графике перемещений, принимаем Smax=80 мм. Тогда:
Масштаб диаграммы скоростей:
где µv – масштабный коэффициент диаграммы скоростей, м∙с-1/мм; µS – масштабный коэффициент диаграммы перемещений, м/мм; µt – масштабный коэффициент времени на диаграмме, с/мм. Нv – полюсное расстояние (принимаем Нv=25 мм). Тогда:
Масштаб диаграммы ускорений:
где µa – масштабный коэффициент диаграммы ускорений, м∙с-2/мм; µv – масштабный коэффициент диаграммы скоростей, м∙с-1/мм; µt – масштабный коэффициент времени на диаграмме, с/мм. Нa – полюсное расстояние (принимаем Нa=30 мм).
Диаграмма перемещений представлена на Рис. 4. 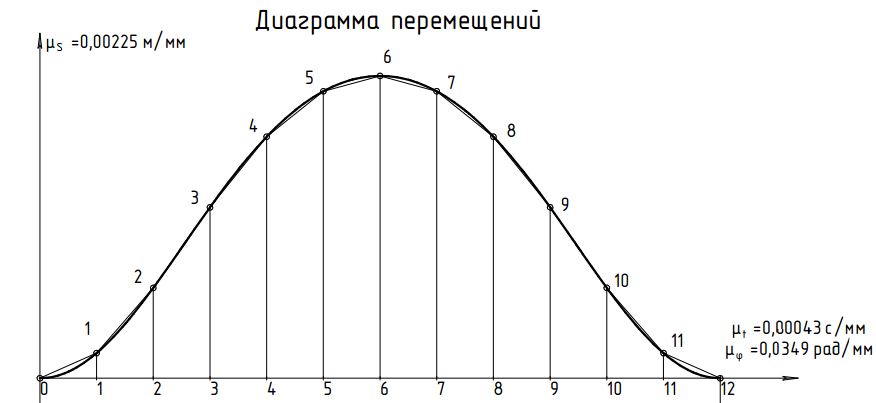 Рис. 4 Диаграмма перемещений Диаграмма скоростей представлена на Рис. 5. 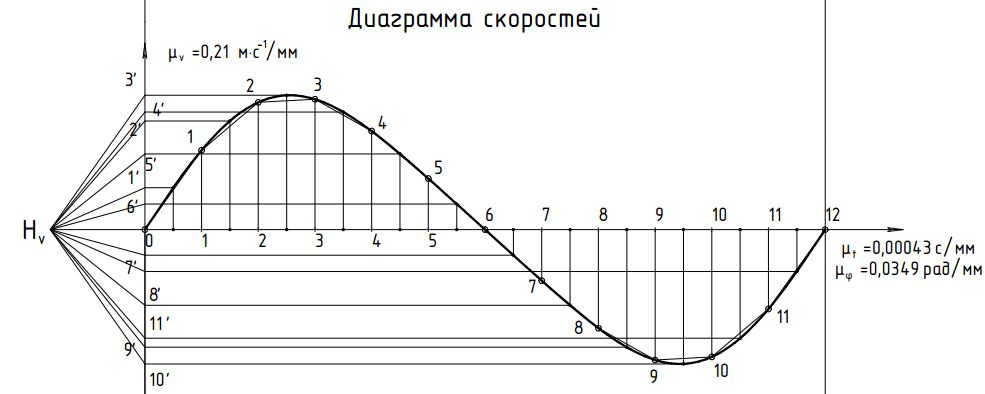 Рис. 5 Диаграмма скоростей Диаграмма ускорений представлена на Рис. 6. 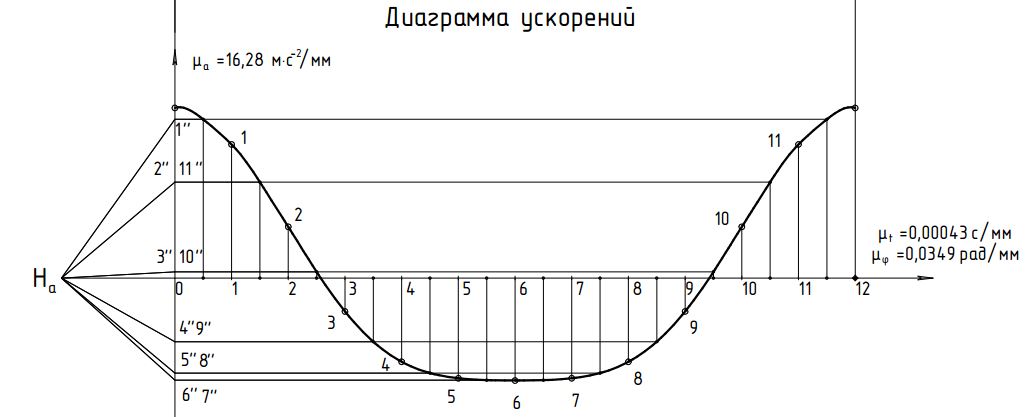 Рис. 6 Диаграмма ускорений |