Методы решения задач линейного программирования. курсовая работа. Курсовая работа по дисциплине "Информационные технологии на транспорте" на тему "Методы решения задач линейного программирования (

• Название: Курсовая работа по дисциплине "Информационные технологии на транспорте" на тему "Методы решения задач линейного программирования (
• Анкор: Методы решения задач линейного программирования
• Дата: 27.05.2022
• Размер: 395.9 Kb.
• Имя файла: курсовая работа.docx
• Тип: Курсовая; #553557
• страница: 1 из 3

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ПЕНЗЕНСКИЙ ГОСУДАРСТВЕННЫЙУНИВЕРСИТЕТ

Кафедра «Транспортные машины»

Курсовая работа

по дисциплине “Информационные технологии на транспорте” на тему “Методы решения задач линейного программирования (Вариант 16)”

Направление подготовки – 23.03.01 Технология транспортных процессов

Профиль подготовки – Организация и безопасность движения

Выполнил студент:___________Потапов А.В.

Группа:15МГ1
Руководитель: к.т.н.,доцент_______Литвинская О.С.


Работа защищена с оценкой

Преподаватели __________

__________

__________

Дата защиты __________


2017

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФГБОУ ВО «Пензенский государственный университет»

Политехнический институт

Факультет "Машиностроения и транспорта"

Кафедра «Транспортные машины»

"УТВЕРЖДАЮ"

Заведующий кафедрой ТМ

_____________В.В. Салмин
ЗАДАНИЕ

на курсовую работу по дисциплине «Информационные технологии на транспорте»
Тема курсовой работы:_ «Методы решения задач линейного программирования»_________

____________________________________________________________________________________________________________________________________________________________
Выдано студенту______Потапову А.В.___________________________ группа __15МГ1__
1. Структура курсовой работы

1.1. Расчетно-пояснительная записка

Введение «Обоснование актуальности темы работы». 1 – 2 стр.

1 Глава. «Постановка задачи». –2 - 5 стр.

2 Глава. «Графический метод » - 5 – 10 стр.

3 Глава. «Метод нахождения опорных планов» - 2 – 8 стр.

4 Глава «Симплекс-метод»-2-10 стр.

5 Глава «Метод потенциалов»-5-10 стр.

6 Глава «Реализация задачи линейного программирования в пакете Microsoft Excel»-5-10 стр.

7 Глава «Сравнительный анализ методов»-1-2 стр.

Заключение (общие выводы). – 1стр.
1.2. Графическая часть

1. 
   Лист. Постановка задачи – формат А1.
   

1.3. Список рекомендуемой литературы

1. 
   Прикладные информационные технологии: Учебное пособие / Е.Л. Федотова, Е.М. Портнов. - М.: ИД ФОРУМ: НИЦ ИНФРА-М, 2013. - 336 с.
   
2. 
   Лунгу, К.Н. Линейное программирование. Руководство к решению задач [Электронный ресурс] : учеб. пособие — Электрон. дан. — Москва : Физматлит, 2009. — 132 с.
   
3. 
   Советов, Б.Я. Информационные технологии: теоретические основы [Электронный ресурс] : учеб. пособие / Б.Я. Советов, В.В. Цехановский. — Электрон. дан. — Санкт-Петербург : Лань, 2017. — 444 с.
   
4. 
   Семь безопасных информационных технологий [Электронный ресурс] : учеб. / А.В. Барабанов [и др.]. — Электрон. дан. — Москва : ДМК Пресс, 2017. — 224 с.
   

1.4. Срок сдачи курсовой работы «__» _ _ 2017 г.

Задание выдал:

к.т.н., доцент Литвинская О.С.

Дата выдачи задания «____» ___________ 20__ г.

Оглавление

введение…………………………………………………………………………………..	5
1 Постановка задач линейного программирования……………………	7
1.1 Стандартная форма модели………………………………………………………………	8
1.2 Каноническая форма модели…………………………………………………………….	8
1.3 Переход от одной формы модели задачи линейного программирования к другой….	8
2 ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ……………………………………………………………………	10
2.1 Алгоритм графического метода решения задач линейного программирования……..	10
2.2 Возможные случаи допустимых решений………………………………………………	11
2.3 Геометрическая интерпретация решения индивидуальной задачи……………………	13
3 Методы нахождения опорных планов………………………………………	17
3.1 Свойства допустимых планов задачи линейного программирования…………………	20
4. Симплекс-метод………………………………………………………………………	21
4.1 Алгоритм симплекс-метода………………………………………………………………	22
4.2 Решение индивидуального задания……………………………………………………..	22
5 Метод потенциалов…………………………………………………………………	31
5.1 Алгоритм метода………………………………………………………………………….	31
5.2 Решение индивидуального задания……………………………………………………..	32
6. Реализация решения задачи линейного программирования в пакете Microsoft Excel………………………………………………………………	36
6.1 Графическая реализация…………………………………………………………………	36
6.2 Реализация симплекс-метода ……………………………………………………………	38
6.3 Реализация метода потенциалов…………………………………………………………	39
7. Сравнительный анализ методов………………………………………………	41
Заключение……………………………………………………………………………….	42
Литература…………………………………………………………………………………	43
ПРИЛОЖЕНИЕ А- Результат проверки работы на антиплагиат…………………………..	44
ПРИЛОЖЕНИЕ Б – Постановка задачи……………………………………………………	45

введение

Цель курсовой работы ознакомиться с методами решения задач линейного программирования: графический метод, симплекс метод, метод потенциалов, а так же произвести расчёты выше перечисленными методами в программном обеспечении «Excel».

Линейное программирование – направление математики, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием оптимальности.

Несколько слов о самом термине линейное программирование. Он требует правильного понимания. В данном случае программирование - это, конечно, не составление программ для ЭВМ. Программирование здесь должно интерпретироваться как планирование, формирование планов, разработка программы действий.

К математическим задачам линейного программирования относят исследования конкретных производственно-хозяйственных ситуаций, которые в том или ином виде интерпретируются как задачи об оптимальном использовании ограниченных ресурсов.

Круг задач, решаемых при помощи методов линейного программирования достаточно широк. Это, например:

1. 
   задача об оптимальном использовании ресурсов при производственном планировании;
   
2. 
   задача о смесях (планирование состава продукции);
   
3. 
   задача о нахождении оптимальной комбинации различных видов продукции для хранения на складах (управление товарно-материальными запасами или "задача о рюкзаке");
   
4. 
   транспортные задачи (анализ размещения предприятия, перемещение грузов).
   

Линейное программирование – наиболее разработанный и широко применяемый раздел математического программирования (кроме того, сюда относят: целочисленное, динамическое, нелинейное, параметрическое программирование). Это объясняется следующим:

1. 
   математические модели большого числа экономических задач линейны относительно искомых переменных;
   
2. 
   данный тип задач в настоящее время наиболее изучен. Для него разработаны специальные методы, с помощью которых эти задачи решаются, и соответствующие программы для ЭВМ;
   
3. 
   многие задачи линейного программирования, будучи решенными, нашли широкое применение;
   
4. 
   некоторые задачи, которые в первоначальной формулировке не являются линейными, после ряда дополнительных ограничений и допущений могут стать линейными или могут быть приведены к такой форме, что их можно решать методами линейного программирования.
   

1 Постановка задач линейного программирования

Для решения задач линейного программирования составляется математическая модель задачи и выбирается метод решения.

Постановка задачи может быть записана в виде математической модели линейного программирования, если целевая функция представлена в виде линейной формы, а связь с ограниченными ресурсами описать посредством линейных уравнений или неравенств. Кроме того, вводится дополнительное ограничение – значения переменных должны быть неотрицательны, поскольку они представляют такие величины, как товарооборот, время работы, затраты и другие экономические показатели.

Геометрическая интерпретация экономических задач даёт возможность наглядно представить, их структуру, выявить особенности и открывает пути исследования более сложных свойств. Задача линейного программирования с двумя переменными всегда можно решить графически. Однако уже в трёхмерном пространстве такое решение усложняется, а в пространствах, размерность которых более трёх, графическое решение, вообще говоря, невозможно. Случай двух переменных не имеет особого практического значения, однако его рассмотрение проясняет свойства задач линейного программирования, приводит к идее её решения, делает геометрически наглядными способы решения и пути их практической реализации.

Индивидуальное задание для решения задач линейного программирования представлено в таблице 1.

Таблица 1 – Исходные данные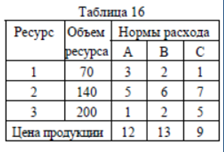



1.1 Стандартная форма модели

Задачами линейного программирования называются оптимизационные задачи, в которых ограничения, представленные в виде равенств или неравенств, и целевая функция линейна. Разработка модели ЛП включает следующие основные этапы: определение переменных задачи, представление её ограничений в виде линейных уравнений или неравенств, задание линейной целевой функции, подлежащей минимизации или максимизации. Стандартная форма имеет вид: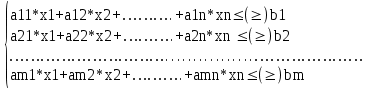

(1)

1.2 Каноническая форма модели

Каноническая форма математической модели имеет вид: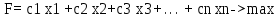

(2)

все переменные Xj — неотрицательны, система ограниче­ний представляет собой систему уравнений, а целевая функция стремится к максимуму, называется канонической формой задачи линейного программирования.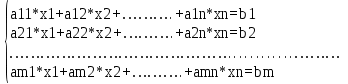

(3)

1.3 Переход от одной формы модели задачи линейного

программирования к другой

Разнообразие форм задач линейного программирования затрудняет исследование их общих особенностей и созда­ние общих методов и вычислительных алгоритмов для их решения. Поэтому естественно рассмотреть способ сведе­ния любой задачи линейного программирования к наиболее простой и удобной для исследования форме — каноничес­кой.

Рассмотрим, каким образом можно перейти от стандарт­ной форме записи к канонической. Для осуществления дан­ного перехода нужно в каждое из m неравенств системы ограничений ввести m дополнительных неотрицательных переменных, тогда система ограниче­ний примет вид: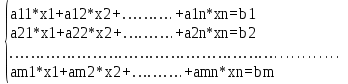

(4)

Если же в стандартной форме требовалось минимизиро­вать целевую функцию, то, заменив ее знак на «-», полу­чим: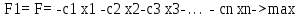

(5)

Таким образом, с помощью представленных преобразо­ваний мы перешли от стандартной формы ЗЛП к ее кано­нической форме.
2. ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Графический метод довольно прост и нагляден для решения задач линейного программирования с двумя переменными. Он основан на геометрическом представлении допустимых решений и ЦФ задачи.

Каждое из неравенств задачи линейного программирования определяет на координатной плоскости (х₁,х₂) некоторую полуплоскость, а система неравенств в целом - пересечение соответствующих плоскостей. Множество точек пересечения данных полуплоскостей называется областью допустимых решений (ОДР). ОДР всегда представляет собой выпуклую фигуру, т.е. обладающую следующим свойством: если две точки А и В принадлежат этой фигуре, то и весь отрезок АВ принадлежит ей. ОДР графически может быть представлена, выпуклым многоугольником, неограниченной выпуклой многоугольной областью, отрезком, лучом, одной точкой. В случае несовместности системы ограничений задачи ОДР является пустым множеством.

2.1 Алгоритм графического метода решения задач линейного программирования

Алгоритм графического метода решения задач линейного программирования представляется следующими шагами:

1. 
   Построить прямые линии, уравнения которых получаем заменой в системе ограничений знаков неравенств на знаки равенств.
   
2. 
   Определить полуплоскости, соответствующие каждому неравенстве задачи.
   
3. 
   Найти многоугольник решений ЗЛП, учитывая, что x₁≥0, x₂≥0.
   
4. 
   Построить вектор направлений g=(с₁,с₂), который указывает направление наибольшего возрастания целевой функции ЗЛП.
   
5. 
   Построить прямую z, которая проходит через область допустимых решений, перпендикулярно к вектору g. Это линия уровня.
   
6. 
   Переместить эту прямую в направлении вектора g в случае максимизации целевой функции (или в противоположном направлении в случае минимизации целевой функции), найти вершину многоугольника решений ЗЛП, в которой целевая функция достигает экстремального значения.
   
7. 
   Определить координаты точки, в которой целевая функция достигает оптимальное значения, и вычислить экстремальное значение целевой функции в этой точке.
   

2.2 Возможные случаи допустимых решений

При графическом построении множества допустимых решений ЗЛП (многоугольника решений) возможны следующие ситуации:

1. Множество допустимых решений – замкнутый многоугольник (рисунок 1):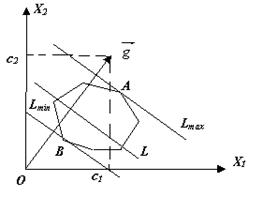



Рисунок 1 – Замкнутый многоугольник

а) оптимальное решение достигается в единственной точке: точка А – точка максимума, точка В – точка минимума;



Рисунок 2. Максимальное значение функции

б) оптимальное решение достигается во всех точках грани (отрезка) многоугольника (рисунок 2): все точки отрезка АВ – оптимальные решения ЗЛП (точки максимума); максимальное значение целевой функции в этом случае находится подстановкой координат любой из этих точек в целевую функцию исходной задачи.

2). Множество допустимых решений – незамкнутый многоугольник: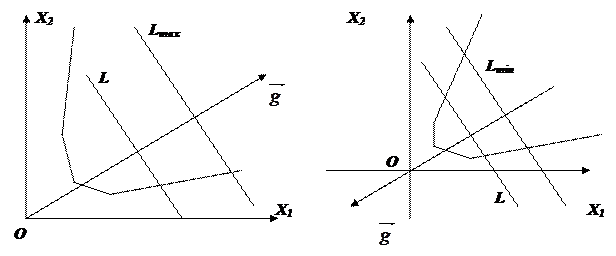


а) б)

Рисунок 3. Незамкнутый многоугольник

В первом случае (рисунок 3, а) целевая функция не ограничена сверху на множестве допустимых решений и поэтому она не достигает своего максимального значения, на втором же рисунке 3,б иллюстрируется случай, когда целевая функция задачи не ограничена снизу на множестве допустимых решений и поэтому она не достигает своего минимального значения.

3) Множество допустимых решений – пустое множество (рисунок 4):