Методы решения задач линейного программирования. курсовая работа. Курсовая работа по дисциплине "Информационные технологии на транспорте" на тему "Методы решения задач линейного программирования (
 Скачать 395.9 Kb. Скачать 395.9 Kb.
|
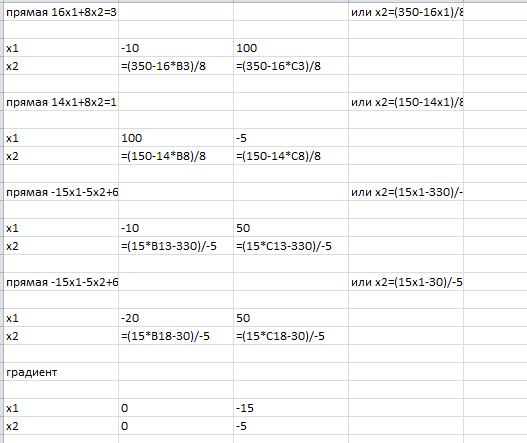 Рисунок 8 Исходные формулы  Рисунок 9 Исходные данные 2. В результате построения графика получили область определения (рисунок 10). 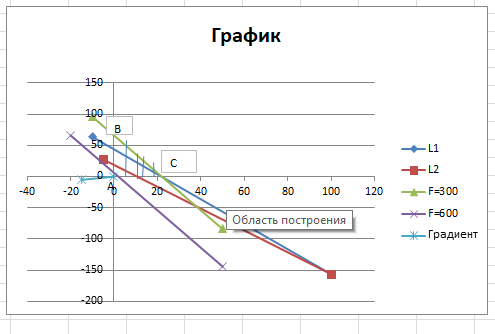 Рисунок 10. Область определений 3 Получение результатов изображено на рисунке 11,12  Рисунок 11. Формула расчёта 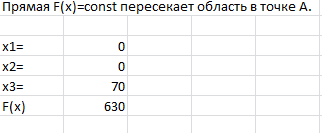 Рисунок 12. Конечный результат 6.2 Реализация симплекс-метода Задаём ограничения в соответствии с индивидуальным вариантом представлено на рисунке 13,14.  Рисунок 13. Исходные формулы 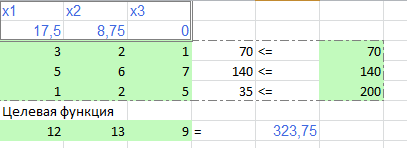 Рисунок 14. Исходные данные С помощью функции «поиск решения» находим максимальное значение представлено на рисунке 15. 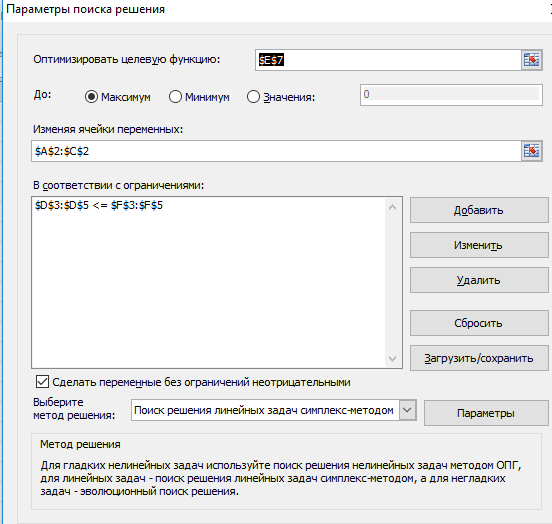 Рисунок 15. Применение функции «Поиск решения» Получение результатов вычисления представлено на рисунке16,. 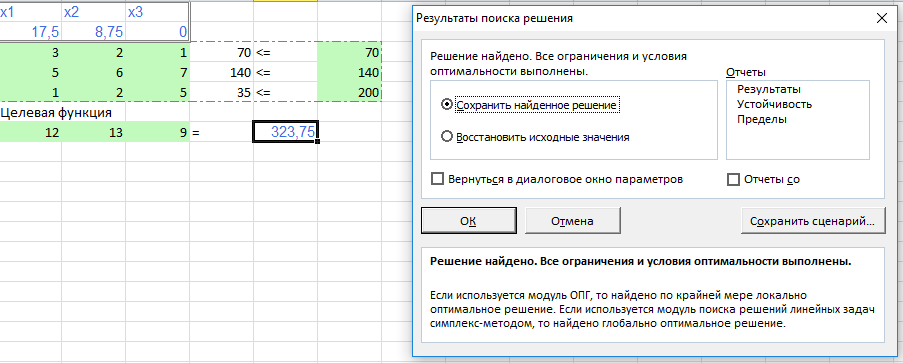 Рисунок 16. Конечный результат 6.3 Реализация метода потенциалов Необходимо задать ограничения в соответствии с индивидуальным заданием представлено на рисунке 17. 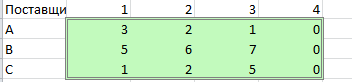 Рисунок 17. Исходные данные С помощью функции «поиск решения» находим максимальное значение изображено на рисунке 18. 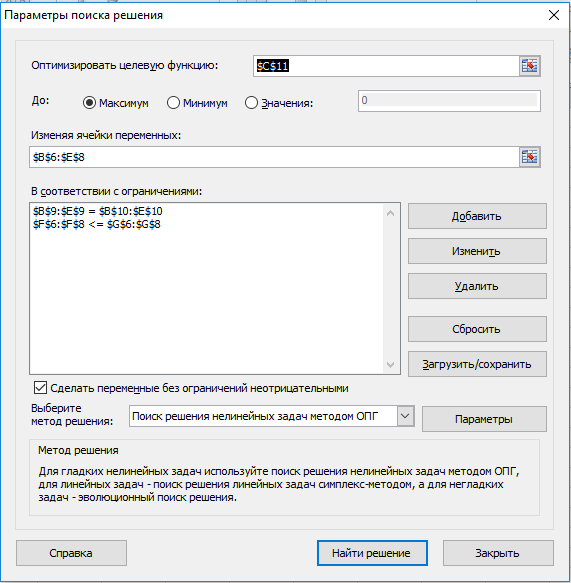 Рисунок 18. Применение функции «исходные данные» Получение результатов вычисления представлено на рисунке 19,20.  Рисунок 19. Формулы расчёта 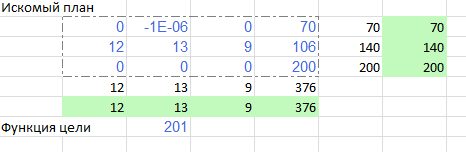 Рисунок 20. Конечный результат 7.СРАВНИТЕЛЬНЫЙ АНАЛИЗ МЕТОДОВ Рассмотренные задачи решены тремя методами: графическим, симплекс-методом и методом потенциалов. Результат полученного ответа получился различным. Решить данную задачу оказалось возможным всеми тремя методами. Первый метод-графический, дает наглядное решение, однако требует предварительного построения уравнений функций и ограничений, а также точного построения графика. Следует отметить, что в данной задаче исходной является система с тремя переменными, а решить такую задачу графическим методом не представляется возможным. Следовательно, необходимо проведение некоторых операций по приведению системы в решаемый вид. Также можно отметить, что достоверность результатов зависит от точности построения графика. Симплекс-метод дает нам более достоверные результаты, так как при его использовании отсутствуют такие серьёзные влияющие факторы(например, как в графическом методе). Однако данный метод требует точного построения таблицы и внесения параметров решения. Метод потенциалов более эффективен по сравнению с графическим методом, а также симплекс-методом. Он имеет ряд преимуществ: В конце расчета получается оптимальный результат. Определяется количество распределённого ресурса. Достоверность результатов зависит от внесения параметров в таблицу. Простота действий по сравнению с симплекс-методом. Заключение В курсовой работе рассмотрены варианты решений транспортных задач методами линейного программирования, в частности графическим методом, симплекс методом и методом потенциалов. В настоящее время линейное программирование является одним из наиболее употребительных аппаратов математической теории оптимального принятия решения. Для решения задач линейного программирования разработано сложное программное обеспечение, дающее возможность эффективно и надежно решать практические задачи больших объемов. Эти программы и системы снабжены развитыми системами подготовки исходных данных, средствами их анализа и представления полученных результатов. Современные методы линейного программирования достаточно надежно решают задачи общего вида с несколькими тысячами ограничений и десятками тысяч переменных. Для решения сверхбольших задач используются уже, как правило, специализированные методы. Список литературы Шапкин А.С., Мазаева Н.П. Математические методы и модели исследования операций: Учебник. – 2-е изд., перераб. и доп. – М.: Дашков и К, 2005. – 400 с. Экономико-математические модели и прогнозирование рынка труда: Учеб. пособие. – М.: Вузовский учебник, 2005. – 144 с. С.И. Шелобаев. Математические методы и модели в экономике, финансах, бизнесе: Учеб. пособие для вузов. – 2-е изд., перераб. и доп. – М.: ЮНИТИ, 2005. – 400 с. Математическая экономика: Учебник для вузов / В.А. Колемаев. – 3-е зд., перераб. и доп. – М.: ЮНИТИ-ДАНА, 2005. – 399 с. М.С.Красс, Б.П.Чупрынов. Математика для экономистов. – М.: Питер, 2004. - 464 с. Солодовников А.С. Математика в экономике: Учебник: в 2-х частях / А.С. Солодовников, В.А. Бабайцев, А.В. Браилов. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2003. – 560 с. Введение в экономико-математические модели налогообложения: Учеб. пособие / Под ред. Д.Г. Черника. – М.: Финансы и статистика, 2002. – 256 с. Ляшенко И.Н., Карагодова Е.А. Линейное и нелинейное программирование. «Вища школа», 1975. - 369 с. Заславский Ю.Л. Сборник задач по линейному программированию. М. 1969-256 с. П.Е.Данко, А.Г. Попов высшая математика в упражнениях и задачах. Ч. 3. М., «Высшая школа», 1971-288 с. В.А.Абчук Экономико-математические методы «Союз» Санкт-Петербург 1999-318 с. |
