Методы решения задач линейного программирования. курсовая работа. Курсовая работа по дисциплине "Информационные технологии на транспорте" на тему "Методы решения задач линейного программирования (
 Скачать 395.9 Kb. Скачать 395.9 Kb.
|
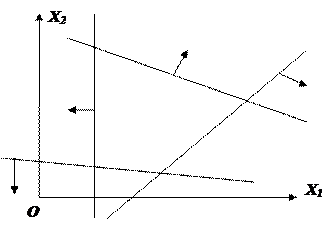 Рисунок 4. Множество допустимых решений Данная ЗЛП решений не имеет. 2.3 Геометрическая интерпретация решения индивидуальной задачи Составим математическую модель задачи. Обозначим х1,х2,х3- количество изделий соответственно вида А,В,С запланированных к производству. Так как имеются ограничения на сырье каждого вида, то переменные х1,х2,х3 должны удовлетворять следующей системе неравенств: 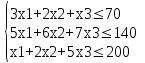 (6) (6)По своему экономическому содержанию переменные 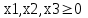 (7) (7)Общая прибыль при этом составит 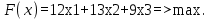 (8) (8)Данная система состоит из 3-х переменных и не решается графическим методом. Поэтому надо привести её к системе с двумя переменными. Выражаем из данной системы неравенств переменную x3 из уравнения 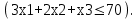 (9) (9)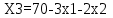 (10) (10)Подставляем получившееся значение в оставшиеся два уравнения и в целевую функцию. В итоге получаем следующую систему уравнений и целевую функцию: 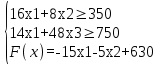 (11) (11)Необходимо найти максимальное значение целевой функции при системе ограничений: 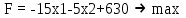 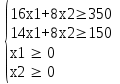 (12) (12)Шаг №1. Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом). Построим уравнение 16x1+8x2 = 350 по двум точкам. Для нахождения первой точки приравниваем x1 = 0. Находим x2 = 43.75. Для нахождения второй точки приравниваем x2 = 0. Находим x1 = 21.88. Соединяем точку (0;43.75) с (21.88;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости: 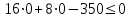 (13) (13)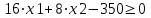 (14) (14)т.е. в полуплоскости выше прямой. Построим уравнение 14x1+8x2 = 150 по двум точкам. Для нахождения первой точки приравниваем x1 = 0. Находим x2 = 18.75. Для нахождения второй точки приравниваем x2 = 0. Находим x1 = 10.71. Соединяем точку (0;18.75) с (10.71;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости: 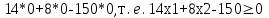 (15) (15)в полуплоскости выше прямой (рисунок 5). 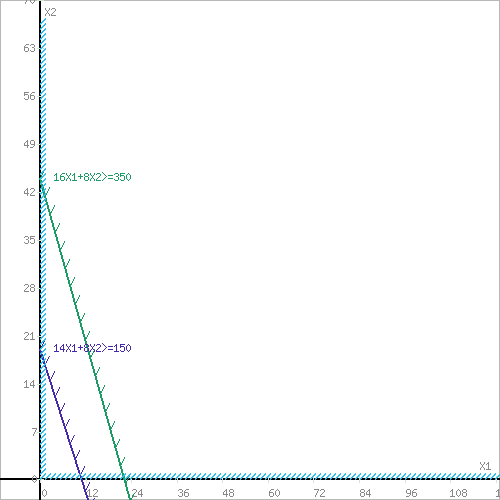 Рисунок 5. График заданных прямых Шаг №2 Границы области допустимых решений. Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи. Обозначим границы области многоугольника решений (рисунок6). 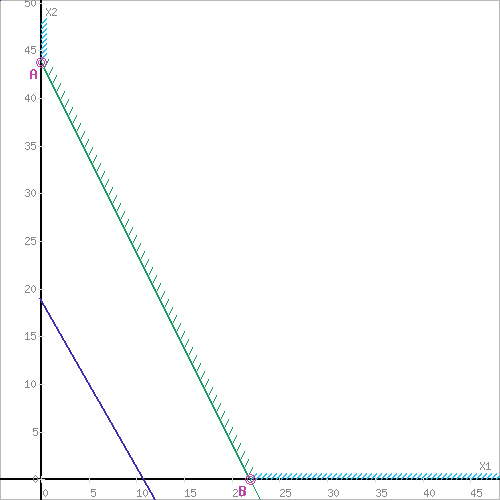 Рисунок 6. График заданных прямых Шаг №3. Рассмотрим целевую функцию задачи F = -15x1-5x2+630 → max. Построим прямую, отвечающую значению функции F = -15x1-5x2+630 = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (-15;-5). Будем двигать эту прямую параллельным образом. Поскольку при расчетах используется значение максимального решения, двигаем прямую до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией (Рисунок7). 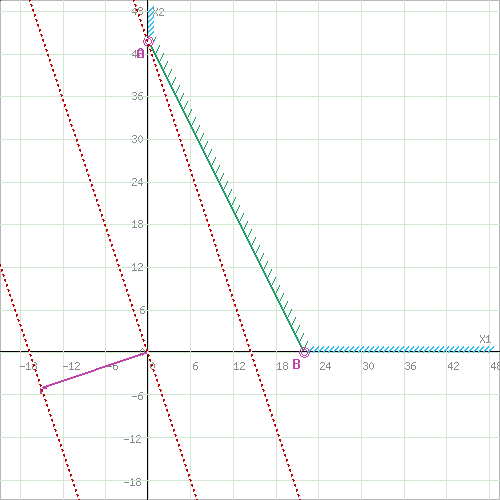 Рисунок 7. График заданных прямых 3.Методы нахождения опорных планов Опорный план является допустимым решением ТЗ и используется в качестве начального базисного решения при нахождении оптимального решения методом потенциалов. Существует три метода нахождения опорных планов: метод северо-западного угла, метод минимального элемента и метод Фогеля. "Качество" опорных планов, полученных этими методами, различается: в общем случае метод Фогеля дает наилучшее решение (зачастую оптимальное), а метод северо-западного угла - наихудшее. Все существующие методы нахождения опорных планов отличаются только способом выбора клетки для заполнения. Само заполнение происходит одинаково независимо от используемого метода. Следует помнить, что перед нахождением опорного плана транспортная задача должна быть сбалансирована. Метод северо-западного угла. Суть метода заключается в следующем. На каждом шаге метода северо-западного угла из всех не вычеркнутых клеток выбирается самая левая и верхняя (северо-западная) клетка. Другими словами, на каждом шаге выбирается первая из оставшихся не вычеркнутых строк и первый из оставшихся не вычеркнутых столбцов. Для того, чтобы заполнить клетку (ij), необходимо сравнить текущий запас товара в рассматриваемой i-й строке аiтек с текущей потребностью в рассматриваемом j-том столбце bjтек. Если существующий запас позволяет перевезти всю потребность, то - в клетку (i,j) в качестве перевозки вписывается значение потребности bjтек, j-й столбец вычеркивается, поскольку его потребность уже исчерпана; от существующего запаса в i-й строке отнимается величина сделанной перевозки, прежний запас зачеркивается, а вместо него записывается остаток, т.е. (аiтек -bjтек ) Если существующий запас не позволяет перевезти всю потребность, то в клетку (i,j) в качестве перевозки вписывается значение запаса аiтек; i-я строка вычеркивается, поскольку ее запас уже исчерпан; от существующей потребности в j-й строке отнимается величина сделанной перевозки, прежняя потребность зачеркивается, а вместо нее записывается остаток, т.е. (bjтек - аiтек). Нахождение опорного плана продолжается до тех пор, пока не будут вычеркнуты все строки и столбцы. Метод минимального элемента. Суть метода заключается в следующем. На каждом шаге метода минимального элемента из всех не вычеркнутых клеток транспортной матрицы выбирается клетка с минимальной стоимостью перевозки. Заполнение выбранной клетки производится по правилам, описанным выше. Метод Фогеля На каждом шаге метода Фогеля для каждой i-й строки вычисляются штрафы dj как разность между двумя наименьшими тарифами строки. Таким же образом вычисляются штрафы dj для каждого j-ro столбца. После чего выбирается максимальный штраф из всех штрафов строк и столбцов. В строке или столбце, соответствующем выбранному штрафу, для заполнения выбирается не вычеркнутая клетка с минимальным тарифом min cij. Если существует несколько одинаковых по величине максимальных штрафов в матрице, то в соответствующих строках или столбцах выбирается одна не вычеркнутая клетка с минимальным тарифом min cij. Если клеток с минимальным тарифом также несколько, то из них выбирается клетка (i,j) с максимальным суммарным штрафом, т.е. суммой штрафов по i-й строке и j-му столбцу. 3.1 Свойства допустимых планов задачи линейного программирования Свойства допустимых планов задачи линейного программирования: 1. Допустимое множество задачи ЛП либо пусто, либо является выпуклым многогранником в Rn (как пересечение полупространств, описываемых неравенствами). Оно может быть как ограниченным, так и неограниченным; в любом случае это замкнутый многогранник. 2. Если допустимое множество не пусто, а целевая функция ограничена сверху (для задачи максимизации, а для задачи минимизации - ограничена снизу) на этом множестве, то задача ЛП имеет оптимальное решение. 3. Оптимальные решения задачи ЛП (если они существуют) всегда находятся на границе допустимого множества. Точнее, если существует единственное оптимальное решение, то им является какая-либо вершина многогранника допустимых решений; если две или несколько вершин являются оптимальными решениями, то любая их выпуклая комбинация также является оптимальным решением (т.е. существует бесконечное множество точек максимума или минимума). Методами решения задач ЛП являются: графический метод (в случае двух переменных), симплекс-метод или его разновидности (в общем случае). 4. СИМПЛЕКС МЕТОД Основным алгоритмом решения ЗЛП является симплекс-метод. Его можно применять в случае, если задача оптимизации записана в специальном каноническом виде. При этом все ограничения имеют вид равенств и каждая базисная переменная встречается с коэффициентом 1 только в одном уравнении, а в других коэффициент при базисной переменной равен 0. Аналитическое выражение для целевой функции не должно содержать базисных переменных, а выражаться только через свободные переменные. Если при этом bi ≥ 0, то говорят о допустимом каноническом виде. Суть симплекс-метода заключается в направленном переборе вершин ОДР с целью определения координат такой вершины, в которой целевая функция достигает экстремума. Введем несколько определений. Опорным решением системы ограничений называется такое решение, когда для системы ограничений в допустимом каноническом виде все свободные переменные равны нулю. Вырожденное опорное решениеопорное решение, в котором одна или несколько базисных переменных равны нулю. Допустимое опорное решениеопорное решение, в котором все базисные переменные ≥ 0. Оптимальное решение ЗЛП будет соответствовать одному из допустимых опорных решений. В симплекс-методе, начиная с допустимого опорного решения, расположенного в вершине многогранника ОДР, переходят к соседней вершине, сохраняя допустимость решения. В симплекс-методе требуется иметь исходное допустимое опорное решение. Иногда такое решение получить легко. Например, если существует ограничение вида 4.1 Алгоритм Симплекс метода Алгоритм метода заключается в следующем: Шаг 1. Привести задачу линейного программирования к канонической форме. Для этого перенести свободные члены в правые части (если среди этих свободных членов окажутся отрицательные, то соответствующее уравнение или неравенство умножить на - 1) и в каждое ограничение ввести дополнительные переменные (со знаком "плюс", если в исходном неравенстве знак "меньше или равно", и со знаком "минус", если "больше или равно"). Шаг 2. Если в полученной системе m уравнений, то m переменных принять за основные, выразить основные переменные через неосновные и найти соответствующее базисное решение. Если найденное базисное решение окажется допустимым, перейти к допустимому базисному решению. Шаг 3. Выразить функцию цели через неосновные переменные допустимого базисного решения. Если отыскивается максимум (минимум) линейной формы и в её выражении нет неосновных переменных с отрицательными (положительными) коэффициентами, то критерий оптимальности выполнен и полученное базисное решение является оптимальным - решение окончено. Если при нахождении максимума (минимума) линейной формы в её выражении имеется одна или несколько неосновных переменных с отрицательными (положительными) коэффициентами, перейти к новому базисному решению. Шаг 4. Из неосновных переменных, входящих в линейную форму с отрицательными (положительными) коэффициентами, выбирают ту, которой соответствует наибольший (по модулю) коэффициент, и переводят её в основные. Переход к шагу 2. 4.2 Решение индивидуального задания Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы. Определим максимальное значение целевой функции при следующих условиях-ограничений F(X) = 12x1+13x2+9x3 3x1+2x2+x3≤70 5x1+6x2+7x3≤140 (16) x1+2x2+5x3≤200 Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных. В 1-м неравенстве смысла (≤) вводим базисную переменную x4. В 2-м неравенстве смысла (≤) вводим базисную переменную x5. В 3-м неравенстве смысла (≤) вводим базисную переменную x6. 3x1+2x2+x3+x4 = 70 5x1+6x2+7x3+x5 = 140 (17) x1+2x2+5x3+x6 = 200 Матрица коэффициентов A = a(ij) этой системы уравнений представлена выражением A= 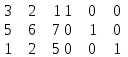  (18) (18)Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом. Решим систему уравнений относительно базисных переменных: x4, x5, x6 Полагая, что свободные переменные равны 0, получим первый опорный план: X0 = (0,0,0,70,140,200) Базисное решение называется допустимым, если оно неотрицательно (таблица 2) Таблица 2 – Базисное решение
Переходим к основному алгоритму симплекс-метода. Итерация №0. 1. Проверка критерия оптимальности. Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты. 2. Определение новой базисной переменной. В качестве ведущего выберем столбец, соответствующий переменной x2, так как это наибольший коэффициент по модулю. 3. Определение новой свободной переменной. Вычислим значения Di по строкам как частное от деления: bi / ai2 и из них выберем наименьшее: min (70 : 2 , 140 : 6 , 200 : 2 ) = 23.333 Следовательно, 2-ая строка является ведущей. Разрешающий элемент равен (6) и находится на пересечении ведущего столбца и ведущей строки представлена в таблице 3. Таблица 3. Базисное решение
4 . Пересчет симплекс-таблицы. Формируем следующую часть симплексной таблицы. Вместо переменной x5 в план 1 войдет переменная x2. Строка, соответствующая переменной x2 в плане 1, получена в результате деления всех элементов строки x5 плана 0 на разрешающий элемент РЭ=6. На месте разрешающего элемента получаем 1. В остальных клетках столбца x2 записываем нули. Таким образом, в новом плане 1 заполнены строка x2 и столбец x2. Все остальные элементы нового плана 1, включая элементы индексной строки, определяются по правилу прямоугольника. Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ: НЭ = СЭ - (А*В)/РЭ, () где СТЭ - элемент старого плана, РЭ - разрешающий элемент (6), А и В - элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ. Представим расчет каждого элемента в виде таблицы 3. Таблица 4. Решение новой симплекс таблицы
Получаем новую симплекс-таблицу 5: Таблица 5 Новая симплекс- таблица
Итерация №1. 1. Проверка критерия оптимальности. Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты. 2. Определение новой базисной переменной. В качестве ведущего выберем столбец, соответствующий переменной x1, так как это наибольший коэффициент по модулю. 3. Определение новой свободной переменной. Вычислим значения Di по строкам как частное от деления: bi / ai1 и из них выберем наименьшее: min (23.333 : 1.333 , 23.333 : 0.833 , - ) = 17.5 Следовательно, 1-ая строка является ведущей. Разрешающий элемент равен (1.333) и находится на пересечении ведущего столбца и ведущей строки представлена в таблице 6. Таблица 6 Базисное решение
4. Пересчет симплекс-таблицы. Формируем следующую часть симплексной таблицы. Вместо переменной x4 в план 2 войдет переменная x1. Строка, соответствующая переменной x1 в плане 2, получена в результате деления всех элементов строки x4 плана 1 на разрешающий элемент РЭ=1.333. На месте разрешающего элемента получаем 1. В остальных клетках столбца x1 записываем нули. Таким образом, в новом плане 2 заполнены строка x1 и столбец x1. Все остальные элементы нового плана 2, включая элементы индексной строки, определяются по правилу прямоугольника. Представим расчет каждого элемента в виде таблицы 7 . Таблица 7 Пересчёт симплекс таблицы
Получаем новую симплекс-таблицу 8: Таблица 8. Новая симплекс-таблица
1. Проверка критерия оптимальности. Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи. Окончательный вариант симплекс-таблицы 9: Таблица 9. Окончательный вариант симплекс-таблицы
Оптимальный план можно записать так: x1 = 17.5, x2 = 8.75, x3 = 0 F(X) = 12•17.5 + 13•8.75 + 9•0 = 323.75 5. МЕТОД ПОТЕНЦИАЛОВ Метод потенциалов является модификацией симплекс-метода решения задачи линейного программирования применительно к транспортной задаче. Он позволяет, опираясь от некоторого допустимого решения, получить оптимальное решение за конечное число итераций. 5.1 Алгоритм метода потенциалов 1. Условия задачи запитать в форме распределительной таблицы. 2. Проверить: является ли задача сбалансированной. 3. Построить начальный опорный план. 4. Вычислить потенциалы поставщиков и потребителей (численные значения потенциалов Ui и Vj определяются из системы уравнений, получаемых по всем базисным клеткам плана из равенства Ui+Vj=Cij ). 5. Вычислить оценки свободных клеток плана по формуле Δij=Cij – (Ui+Vj). Если оценки Δij свободных клеток плана – неотрицательны, то план оптимальный. Если же среди оценок есть отрицательные, то построенный план не является оптимальным. Для получения лучшего плана поступают так: 1) Клетку с наименьшей отрицательной оценкой переводят в базисную вместо какой-либо прежней базисной. 2) Для вводимой клетки строится замкнутый цикл; ей приписывается знак «+», а следующей базисной (только в вершинах) по ходу цикла в любом направлении знак «-», затем опять «+» и т.д. 3) В клетках со знаком «-» выбирается наименьшая загрузка, которая перемещается по циклу с прибавлением его в положительных и вычитанием в отрицательных клетках. 4) В итоге одна из базисных клеток становится свободной и образуется новых опорный план, который также проверяется на оптимальность. 5.2 Решение индивидуального задания Исходные данные представлены в пункте № 1. Проверка задачи на закрытость Задача является открытой, соответственно надо привести её к закрытому виду: Объём ресурса>Цена Добавляем дополнительный столбец, элементы которого будут нулевыми, а цена будет равна: Σобъём ресурсов=Σцена Таблица 10. Закрытая исходная таблица
Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов Проверим необходимое и достаточное условие разрешимости задачи. ∑a = 70 + 140 + 200 = 410 (19) ∑b = 12 + 13 + 9 + 376 = 410 (20) Условие баланса соблюдается. Запасы равны потребностям. Следовательно, модель транспортной задачи является закрытой. Этап I. Поиск первого опорного плана 1 . Используя метод наибольшей стоимости, построим первый опорный план транспортной задачи. Суть метода заключается в том, что из всей таблицы стоимостей выбирают наибольшую, и в клетку, которая ей соответствует, помещают меньшее из чисел ai, или bj. Затем, из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся части таблицы стоимостей снова выбирают наибольшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены. В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность потребителей удовлетворена, а план соответствует системе ограничений транспортной задачи представлена в таблице 11. Таблица 11. Система ограничений
Значение целевой функции для этого опорного плана равно: F(x) = 0*70 + 5*12 + 6*13 + 7*9 + 0*106 + 0*200 = 201 2. Подсчитаем число занятых клеток таблицы, их 6, а должно быть m+n-1 = 6. Следовательно, опорный план является невырожденным. Этап II. Улучшение опорного плана Проверим оптимальность опорного плана. Найдем предварительные потенциалы ui, vj. по занятым клеткам (таблица 12), в которых ui + vj = cij, полагая, что u1 = 0. u1 + v4 = 0; 0 + v4 = 0; v4 = 0 u2 + v4 = 0; 0 + u2 = 0; u2 = 0 u2 + v1 = 5; 0 + v1 = 5; v1 = 5 u2 + v2 = 6; 0 + v2 = 6; v2 = 6 u2 + v3 = 7; 0 + v3 = 7; v3 = 7 u3 + v4 = 0; 0 + u3 = 0; u3 = 0 Таблица 12. Проверка оптимального плана
Опорный план является оптимальным, так все оценки свободных клеток удовлетворяют условию ui + vj ≤ cij. Максимальная прибыль составит: F(x) = 0*70 + 5*12 + 6*13 + 7*9 + 0*106 + 0*200 = 201 6. Реализация решения задачи линейного программирования в пакете Microsoft Excel Задачи линейного программирования так же можно решить с помощью программного обеспечения «Microsoft Еxcel» 6.1 Графическая реализация 1. Задаём ограничения в соответствии с индивидуальным вариантом задания на листе Excel представлено на рисунке 8,9 . | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
