Курсовая работа по дисциплине Моделирование систем
 Скачать 0.63 Mb.
|
Задание №33.В модель разместить событие выполняющиеся с интенсивностью =2. При исполнении события генерируется случайное целое число ri из диапазона от 1 до 20. В модель разместить глобальный массив a[N], N=20. В массив заносятся счетчики повторов случайного числа в процессе работы модели в течении 700 единиц модельного времени. Определить частоты Pi сгенерированных случайных чисел. Сумма Pi=1. Вывести график f=(n,Pi) здесь n – число. Задание №34В модель разместить событие выполняющиеся с интенсивностью =2. При исполнении события генерируется случайное целое число ri из диапазона от 1 до 10. В модель разместить глобальный массив a[N], N=10. В массив заносятся счетчики повторов случайного числа в процессе работы модели в течении 700 единиц модельного времени. Определить частоты Pi сгенерированных случайных чисел. Сумма Pi=1. Вывести полученные частоты и определить энтропию полученных статистических данных:  .Задание №35.Дано два глобальных массива a[N] и b[M] вещественных случайных чисел. Значения размерности N=50, M=100. При запуске модели запускается событие e1 с периодом T1=2сек. Для заполнения массивов. После заполнения массивов событие прекращает свою работу. Далее запускаются параллельно два динамических события e2 и e3 с периодами T2=3 сек, T4=4 сек . Первое событие вычисляет значение  а второе событие значение  . Когда оба значения будут вычислены, то запускается динамическое событие e4 с периодом T4=1сек, для вычисления значения Z=Y +X Задание №36.Дана функция f1(x) = ex - 2 и функция f2(x)=8/(x+0,6) - 7. Где x [0.1,...,1.9] с меняется с шагом 0.1. Построить модель для вывода графиков функций, используя динамические события e1 и e2, исполняющиеся с периодами T1 и T2 параллельно. Создать интерфейс модели для задания значений T1 и T2 перед запуском эксперимента модели. Задание №37.Дан словарь – массив кодов a={10,30,90,60,50,70,20}. Разместить в модель динамическое событие e1 которое срабатывает с интенсивностью = 3. Событие - источник данных выбирает в случайном порядке код из словаря. Время работы модели 700 единиц модельного времени, определить частотные характеристики Pi по каждому коду. Сумма Pi = 1. Построить график f(ai,Pi). Задание №38.Дано последовательность чисел f1, f2, f3,... Если эта последовательность построена с помощью рекурсивного соотношения fn = fn-1 + fn-2, для n >2 с начальными значениями f1=f2 =1 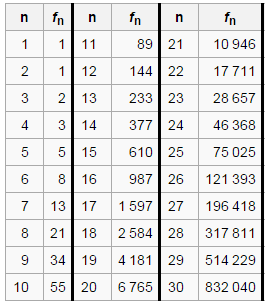 То эта последовательность – последовательность Фибоначчи. Разработать модель с событием е, выполняющимся с периодичностью T для вычисления последовательности Фибоначчи для n=30. В поле модели выводить три числа fn, fn-1, fn-2. Полученную последовательность представить в виде графика f(n,fn). Задание №39.Дано два события e1 и е2 выполняющиеся с периодами T1 и T2. Первое событие – поставщик заполняет буфер массив чисел целого типа a[N], N=50 случайными числами. Когда массив заполнен, событие прекращает свою работу и запускает событие e2 – потребитель, которое заполняет массив нулями. Когда массив заполнен, событие прекращает работу и запускает событие e1. Содержимое массива отображать в виде графика f(j,aj), j. Работа модели происходит циклически, дисциплина работы с массивом - очередь. Работу с буфером показать в виде временного графика – циклограммы f(t,Yi). Когда буфер заполнен Yi=N, при выборке буфера потребителем Yi=0. Задание №40.Создать модель для вычисления числа Эйлера с точностью = 10-6 по формуле  Для вычисления числа использовать динамическое событие выполняющиеся с периодом времени T. Погрешность вычисления представить в виде графика f(n,i). Задание №41.В аудиторскую фирму поступает простейший поток заявок на обслуживание с интенсивностью λ = 1,5 заявки в день. Время обслуживания распределено по показательному закону и равно в среднем трем дням. Аудиторская фирма располагает пятью независимыми бухгалтерами, выполняющими аудиторские проверки (обслуживание заявок). Очередь заявок имеет длину N. Если время обслуживания заявок превышает заданное значение T, то заявка покидает систему. Если очередь заявок занята, то заявка теряется. Заявка поступает из очереди к бухгалтеру случайным образом с вероятностью P. Определить время нахождения заявки в очереди, среднее время обслуживания, среднее число заявок в очереди. Показать движение заявок в очереди и процесс их обслуживания аудиторами. Определить пропускную способность системы массового обслуживания. Построить гистограммы распределения времен. Построить круговую гистограмму распределения долей потерянных заявок, ушедших по таймауту, обслуженных, ожидающих обслуживания. |