Прикладная математика. Курсовик. Вариант 10. Курсовая работа по дисциплине Прикладная математика
 Скачать 0.5 Mb. Скачать 0.5 Mb.
|
|
Если все оценочные коэффициенты (зеленый цвет) неотрицательны, то получено оптимальное решение: базисные переменные равны свободным членам, остальные равны 0, максимум целевой функции указан правее буквы P. Если же есть отрицательный оценочный коэффициент, то находят самый малый из них. Если в столбце коэффициентов над ним нет положительных, то задача не имеет решения. Задача оптимального планирования не может быть таковой, поэтому ищут минимальное отношение свободных членов к положительным элементам указанного столбца (минимальное отношение – выделено жирным шрифтом). Таблица N 2
Если все оценочные коэффициенты (выделены курсивом) неотрицательны, то получено оптимальное решение: базисные переменные равны свободным членам, остальные равны 0, максимум целевой функции указан правее буквы P. Если же есть отрицательный оценочный коэффициент, то находят самый малый из них. Если в столбце коэффициентов над ним нет положительных, то задача не имеет решения. Задача оптимального планирования не может быть таковой, поэтому ищут минимальное отношение свободных членов к положительным элементам указанного столбца (минимальное отношение – выделено жирным шрифтом). Таблица N 3
Оптимальный план: x5= 6.00;x4= 28.00;x1= 40.00; все остальные переменные равны 0 ; максимум целевой функции равен 3340.00 значение переменной с номером i большим 4 есть остаток (i-4)-го ресурса (после выполнения оптимального плана). Так как все оценочные коэффициенты (выделены курсивом) неотрицательны, то получено оптимальное решение: базисные переменные равны свободным членам, остальные равны 0, максимум целевой функции указан правее буквы P. Выше выписан ответ. Задача 1.2.Двойственная задача линейного программирования Задача линейного оптимального планирования - исходная в своей паре симметричных двойственных задач. Вообще же другая задача в двойственной паре строится так: 1)меняется тип экстремума целевой функции ( max на min и наоборот); 2)коэффициенты целевой функции одной задачи становятся свободными членами другой задачи; 3)свободные члены одной задачи становятся коэффициентами целевой функции двойственной задачи ; 4)тип неравенств меняется ( <= на => и наоборот); 5) каждый столбец одной задачи порождает строку ограничений другой задачи и наоборот. В матрично - векторном виде обе задачи выглядят так: исходная задача двойственная задача CX-->max YB-->min AX<=B, X>=0 YA=>C, Y=>0 P= 59*x1+27*x2+20*x3+35*x4-->max S= 102*y1+204*y2+188*y3-->min 1*x1+3*x2+2*x3+2*x4<=102 1*y1+3*y2+4*y3=>59 3*x1+2*x2+0*x3+3*x4<=204 3*y1+2*y2+2*y3=>27 4*x1+2*x2+3*x3+1*x4<=188 2*y1+0*y2+3*y3=>20 x1,x2,x3,x4>=0 2*y1+3*y2+1*y3=>35 y1,y2,y3>=0 Таблица N 3
Исходная задача: x1= 40.00;x2=0;x3=0;x4= 28.00;x5= 6.00;x6=0;x7=0; Оптимальные значения двойственных переменных равны оценочным коэффициентам балансовых переменных исходной задачи, а экстремумы целевых функций равны. Двойственная задача: y1= 0.00;y2= 9.00;y3= 8.00; экстремумы целевых функций исходной и двойственной задач равны 3340.00 (см. таблицу). P= 59*x1+27*x2+20*x3+35*x4-->max S= 102*y1+204*y2+188*y3-->min 1*x1+3*x2+2*x3+2*x4<=102 1*y1+3*y2+4*y3=>59 3*x1+2*x2+0*x3+3*x4<=204 3*y1+2*y2+2*y3=>27 4*x1+2*x2+3*x3+1*x4<=188 2*y1+0*y2+3*y3=>20 x1,x2,x3,x4>=0 2*y1+3*y2+1*y3=>35 y1,y2,y3>=0 Решение одной из пары двойственных задач можно найти, зная только ответ к другой задаче и пользуясь 2-й теоремой двойственности: если i-е ограничение одной из пары двойственных задач на компонентах оптимального решения есть стро- гое неравенство, то оптимальное значение i-й переменной другой задачи равно 0, или, что то же самое - если оптимальное значение j-й переменной одной задачи строго положительно, то j-е ограничение другой из пары двойственных задач на компонентах оптимального решения есть равенство. Проверим решение, используя эту теорему. Исходная задача: x1= 40.00;x2=0;x3=0;x4= 28.00;x5= 6.00;x6=0;x7=0; Двойственная задача: y1= 0.00;y2= 9.00;y3= 8.00 экстремумы целевых функций исходной и двойственной задач равны 3340.00 P= 59*x1+27*x2+20*x3+35*x4-->max S= 102*y1+204*y2+188*y3-->min 1*x1+3*x2+2*x3+2*x4<=102 1*y1+3*y2+4*y3=>59 3*x1+2*x2+0*x3+3*x4<=204 3*y1+2*y2+2*y3=>27 4*x1+2*x2+3*x3+1*x4<=188 2*y1+0*y2+3*y3=>20 x1,x2,x3,x4>=0 2*y1+3*y2+1*y3=>35 y1,y2,y3>=0 Задача 1.3.Расшивка узких мест Исходные данные:
При выполнении оптимальной производственной программы второй и третий ресурсы используются полностью, тем самым они образуют "узкие места" производства. Будем их заказывать дополнительно. Пусть T=( 0,t2,t3) - вектор дополнительных объемов ресурсов. Так как мы будем использовать найденные двойственные оценки ресурсов, то должно выполняться условие H+Q^(-1)T>=0 или H>=-Q^(-1)T, где H -значения базисных переменных в последней симплексной таблице, а Q^(-1) - обращенный базис, который образуют столбцы при балансовых переменных в этой таблице. Задача состоит в том, чтобы найти вектор T , максимизирующий суммарный прирост прибыли W= 9t2+ 8t3 при условии сохранения двойственных оценок ресурсов (и, следовательно ассортимента выпускаемой продукции), предполагая, что можно получить дополнительно не более 1/3 первоначального объема ресурсов каждого вида. При выполнении оптимальной производственной программы второй и третий ресурсы используются полностью, т.е. образуют “узкие места производства”. Будем их заказывать дополнительно. Пусть Т(0,t2,t3) – вектор дополнительных объемов ресурсов. Так как используются найденные двойственные оценки, то должно выполняться следующее условие: H + Q-1T ≥ 0. Задача состоит в том, чтобы найти вектор , максимизирующий суммарный прирост прибыли: W= 9t2 + 8t3 при условии сохранения двойственных оценок ресурсов (и, следовательно, структуры производственной программы), предполагая, что можно надеяться получить дополнительно не более 1/3 первоначального объема ресурса каждого вида 0   102 102t2 ≤ 1/3 204 t3 188 , причем по смыслу задачи t2 ≥0, t3 ≥ 0. С  ледовательно, получаем ледовательно, получаем6    1 -0,78 0,33 0 0 1 -0,78 0,33 0 028 + 0 0,44 -0,33 • t2 ≥ 0 40 0 -0,11 0,33 t3 0 . Перемножим матрицы и получим следующую систему неравенств: -   0,78t2 + 0,33t3 ≥ -6, -7t2 + 3t3 ≥ -54, (I) 0,78t2 + 0,33t3 ≥ -6, -7t2 + 3t3 ≥ -54, (I) 0,44t2 – 0,33t3 ≥ -28, 4t2 – 3t3 ≥ -252, (II) -0,11t2 + 0,33t3 ≥ -40, - t2 + 3t3 ≥ -360; (III) t2 ≤ 204/3, t3 ≤ 188/3, t2 ≤34,46, t3 ≤ 62,67, t2 ≥ 0, t3 ≥ 0; t2 ≥ 0, t3 ≥ 0. Решим данную задачу графически. 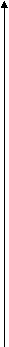 t3 t3  62,67 62,67  0 t2 204/3 Программа “расшивки” имеет вид t2 = 34,46 , t3 = 62,67, и прирост прибыли составит maxW = 9∙242/7+ 8∙188/3 =17062/21 ≈ 811,48 в точке М(34,46;62,67). 1.4. Задача о комплектном плане. Исходные данные: из пункта 1.1. имеем задачу линейного программирования 59 x1 + 27 x2 + 20x3 +35 x4 → max, 1x1 + 3x2 + 2x3 + 2x4 ≤ 102, 3x1 + 2x2 + 0x3 + 3x4 ≤ 204, 4x1 + 2x2 + 3x3 + 1x4 ≤ 188, x1 - 4 ≥ 0. Даны следующие пропорции: x3 x4 — = 2, — = 5, x1 x2 Решение: 1.Предположим, что в данной линейной производственной задаче продукция производится комплектно: 3-го вида продукции необходимо произвести в 2 раза больше, чем 1-го, а 4-го в 5 раз больше, чем второго вида продукции. x3 x4 Т.е. имеем соотношения — = 2, — = 5, или x3 = 2x1 и x4 = 5x2. x1 x2 Подставляя эти выражения x3 и x4 через x1 и x2 в данную линейную производственную задачу, получаем следующее 59x1 + 27x2 + 20∙2x1+35∙5x2 → max, x1 + 3x2 + 2∙2x1 + 2∙5x2 ≤ 102, 3x1 + 2x2 + 0 + 3∙5x2 ≤ 204, 4x1 + 2x2 + 3∙2x1 + 5x2 ≤ 188, x1, х2 ≥ 0. 2. Преобразуем полученную модель к задаче линейного программирования с двумя переменными: 99x1 + 202x2 → max, 5x1 + 13x2 ≤ 102, (I) 3x1 + 17x2 ≤ 204, (II) 10x1 + 7x2 ≤ 188, (III) x1, х2 ≥ 0. Решим полученную задачу графически. 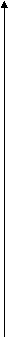 х2 х2 III III     I I     M II M II  0 х1 0 х1 |
