Прикладная математика. Курсовик. Вариант 10. Курсовая работа по дисциплине Прикладная математика
 Скачать 0.5 Mb.
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x1 + 13x2 =102,| x | 0 | 100 | 200 | 300 | 400 | 500 | 600 | 700 |
| f1(x) | 0 | 10 | 20 | 30 | 38 | 43 | 49 | 52 |
| f2(x) | 0 | 13 | 25 | 37 | 47 | 55 | 61 | 66 |
| f3(x) | 0 | 6 | 13 | 20 | 27 | 3 | 38 | 41 |
| f4(x) | 0 | 24 | 36 | 0 | 46 | 48 | 48 | 49 |
| x2 | t f1\F1 | 0 0 | 100 10 | 200 20 | 300 30 | 400 38 | 500 43 | 600 49 | 700 52 |
| 0 | 0 | 0 | 10 | 20 | 30 | 38 | 43 | 49 | 52 |
| 100 | 13 | 13 | 23 | 33 | 43 | 51 | 56 | 62 | |
| 200 | 25 | 25 | 35 | 45 | 55 | 63 | 68 | | |
| 300 | 37 | 37 | 47 | 57 | 67 | 75 | | | |
| 400 | 47 | 47 | 57 | 67 | 77 | | | | |
| 500 | 55 | 55 | 65 | 75 | | | | | |
| 600 | 61 | 61 | 71 | | | | | | |
| 700 | 66 | 66 | | | | | | | |
Жирным шрифтом обозначен максимальный суммарный эффект от выделения соответствующего размера инвестиций 2 предприятиям.
| t | 0 | 100 | 200 | 300 | 400 | 500 | 600 | 700 |
| F2 | 0 | 13 | 25 | 37 | 47 | 57 | 67 | 77 |
| z2 | 0 | 100 | 200 | 300 | 300 | 300 | 300 | 400 |
Таблица N 2
-
x3
t
f2\F2
0
0
100
13
200
25
300
37
400
47
500
57
600
67
700
77
0
100
200
300
400
500
600
700
0
6
13
20
27
3
38
41
0
6
13
20
27
3
38
41
13
19
26
33
40
16
51
25
31
38
45
52
37
43
50
57
64
47
53
60
67
57
63
70
67
73
77
28
Жирным шрифтом обозначен максимальный суммарный эффект от выделения соответ-
ствующего размера инвестиций 3 предприятиям.
-
t
0
100
200
300
400
500
600
700
F3
0
13
25
37
47
57
67
77
z3
0
0
0
0
0
0
0
0
Таблица N 3
-
x4
0
100
200
300
400
500
600
700
t
f3\F3
0
24
36
0
46
48
48
49
0
0
0
24
36
0
46
48
48
49
100
13
13
37
49
13
59
61
61
200
25
25
49
61
25
71
73
300
37
37
61
73
37
83
400
47
47
71
83
47
500
57
57
81
93
600
67
67
91
700
77
77
Жирным шрифтом обозначен максимальный суммарный эффект от выделения соответствующего размера инвестиций 4 предприятиям.
-
t
F4
z4
0
0
0
100
24
100
200
37
100
300
49
100
400
61
100
500
73
200
600
83
200
700
93
200
Сведем результаты в 4 таблицы. Теперь F4(700)=93 показывает максимальный
суммарный эффект по всем 4-м фирмам, а z4(700)=200 - размер инвестиций в 4-ю
фирму для достижения этого максимального эффекта. После этого на долю первых
3-х фирм осталось (700-200) и для достижения максимального суммарного эффекта
по первым 3-м фирмам в 3-ю надо вложить 000 и т.д. Жирным шрифтом
отмечены оптимальные значения инвестиций по фирмам и значения эффектов от них.
-
t
0
100
200
300
400
500
600
700
F1=f1
z1=x1
0
0
10
1
20
200
30
3
38
4
43
5
49
6
52
7
F2
z2
0
0
13
1
25
2
37
3
47
3
57
300
67
3
77
4
F3
z3
0
0
13
0
25
0
37
0
47
0
57
0
67
0
77
0
F4
z4
0
0
24
1
37
1
49
1
61
1
73
2
83
2
93
200
Принятие решений в условиях неопределённости
3.1. Анализ связанного набора операций в условиях неопределенности
Предположим, что ЛПР (Лицо, Принимающее Решения) обдумывает четыре возможных
решения. Но ситуация на рынке неопределенна, она может быть одной из четырех.
С помощью экспертов ЛПР составляет матрицу последствий или доходов Q .
Элемент этой матрицы q[i,j] показывает доход, полученный ЛПР, если им
принято i-е решение, а ситуация оказалась j-я. В этой схеме полной
неопределенности могут быть высказаны лишь некоторые соображения о том, какое
решение принять. Сначала построим матрицу рисков. Строится эта матрица так: в
каждом столбце матрицы доходов находим максимальный элемент d[j] , после чего
элементы r[i,j]=d[j]-q[i,j] и образуют матрицу рисков. Смысл рисков
таков: если бы ЛПР знал что в реальности имеет место j-я ситуация, то он
выбрал бы решение с наибольшим доходом, но он не знает, поэтому, принимая
i-е решение он рискует недобрать d[j]-q[i,j] - что и есть риск.
Задана матрица последствий 4x4 из не более чем двузначных неотрицательных
чисел. Компьютер вычисляет матрицу рисков.
Матрица доходов Матрица рисков
│2 4 6 18│ │0 8 12 4│
│0 8 16 20│ │2 4 2 2│
│2 12 18 22│ │0 0 0 0│
│0 4 10 14│ │2 8 8 8│
Правило Вальда называют правилом крайнего пессимизма: ЛПР уверен, что какое-
бы решение он ни принял, ситуация сложится для него самая плохая, так что,
принимая i-е решение, он получит минимальный доход q[i]=min{q[i,j]:j=1..4}.
Но теперь уже из чисел q[i] ЛПР выбирает максимальное и принимает соответствующее решение.
По правилу Сэвиджа находят в каждой строке матрицы рисков максимальный
элемент r[i] и затем из чисел r[i] находят минимальное и принимают соответствующее решение. Так принимает решение ЛПР, не любящий рисковать.
По правилу Гурвица для каждой строки матрицы доходов находят величину
z[i]=a*max{q[i,j]:j=1..4}+(1-a)*min{q[i,j]:j=1..4}, потом находят из чисел
z[i] наибольшее и принимают соответствующее решение. Число a каждый ЛПР
выбирает индивидуально - оно отражает его отношение к доходу и риску, при
приближении a к 0 правило Гурвица приближается к правилу Вальда, при
приближении a к 1 - к правилу розового оптимизма, в нашем случае a равно 1/2.
Матрица доходов Матрица рисков
Вальд-► 2 2 │2 4 6 18│10.0 12│0 8 12 4│
0 │0 8 16 20│10.0 4 │2 4 2 2 │
2 │2 12 18 22│12.0 12.0 ◄-Гурвиц Сэвидж-► 0 0 │0 0 0 0 │
0 │0 4 10 14│ 7.0 8 │2 8 8 8 │
3.2.Анализ связанного набора операций в вероятностных условиях
Предположим, что ЛПР (Лицо, Принимающее Решения) обдумывает четыре возможных
решения. Но ситуация на рынке неопределенна, она может быть одной из четырех.
Однако в отличие от предыдущей опции известны вероятности этих ситуаций p[j].
Имея матрицу доходов Q теперь можно сказать, что доход от i-го решения
есть с.в. Q[i] с доходами q[i,j] и вероятностями этих доходов p[j].
Кроме того, риск i-го решения также есть с.в. R[i] с рисками r[i,j] и
вероятностями этих рисков p[j]. Математические ожидания с.в. Q[i], R[i]
называются также средним ожидаемым доходом и средним ожидаемым риском i-го
решения. Теперь можно принять решение (провести операцию), у которого наибольший средний ожидаемый доход, или наименьший средний ожидаемый риск. Вероятности p[j] - обыкновенные дроби вида 1/4 или 1/12.
матрица доходов доход средний ожидаемый риск матрица рисков
│2 4 6 18│ 6.8 6.4 │ 0 8 12 4 │
│0 8 16 20│10.4 2.8 │ 2 4 2 2 │
│2 12 18 22│13.2 ◄-max min-► 0.0 │ 0 0 0 0 │
│0 4 10 14│ 6.4 6.8 │ 2 8 8 8 │
── ── ── ── ── ── ── ──
1/5 2/5 1/5 1/5 1/5 2/5 1/5 1/5
вероятности ситуаций вероятности ситуаций
Для уточнения распределения вероятностей можно провести пробную операцию.
После ее проведения вероятности состояний, характеристики операций и оптимальные решения могут стать совершенно иными.
Жирным шрифтом выделены первоначальные характеристики, подчёркнутым - после проведения пробной операции. Подсчитаем, при какой максимальной
стоимости пробная операция еще оправдана, если решение принимать по критерию
максимального среднего ожидаемого дохода.
Первоначальные вероятности и характеристики операции
вероятности ситуаций вероятности ситуаций
1/5 2/5 1/5 1/5 1/5 2/5 1/5 1/5
доход средний ожидаемый риск ───
матрица доходов ▼ до пробной операции ▼ матрица рисков
│ 2 4 6 18 │ 6.8 16.4 3.6 6.4 │ 0 8 12 4 │
│ 0 8 16 20 │ 10.4 18.0 2.0 2.8 │ 2 4 2 2 │
│ 2 12 18 22 │ 13.2 20.0 0.0 0.0 │ 0 0 0 0 │
│ 0 4 10 14 │ 6.4 12.6 7.4 6.8 │ 2 8 8 8 │
── ── ── ── ── ── ── ──
0.1 0.0 0.0 0.9 ▲ после операции ▲ 0.1 0.0 0.0 0.9
вероятности ситуаций вероятности ситуаций
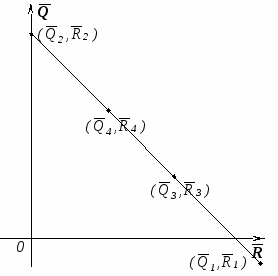
3.3.Анализ по доходу и риску набора операций
Пусть имеем набор несвязанных друг с другом операций Q[i], i=1..n . Каждая
операция имеет два показателя: доход m[i] и риск r[i]. Скажем, что i-я операция
доминирует (превосходит) j-ю, если m[i]>=m[j] и r[i]<=r[j] и хотя бы одно из
этих неравенств строгое. При выборе наилучшей операции стараются, чтобы доход
был больше, а риск меньше, поэтому ни при каком разумном выборе доминируемая
операция не может быть выбрана. Остаются недоминируемые операции. Они называются оптимальными по Парето. Заданы характеристики 6-и операций. Жирным шрифтом выделены доминируемые операции и подчёркнутым - недоминируемые, т.е.
оптимальные по Парето. Ниже описано начало координат
плоскости (r,m) : риск - по горизонтали вправо, доход - по вертикали вверх.
Доход и риск операций
123456
доход xx<=20 14 3 15 10 11 8
риск xx<80 9 20 11 8 71 68
Анализ доходности и рискованности финансовых операций
4.1.Доходность и риск операции вероятностно характеризуемой
Финансовая операция называется рискованной, если она имеет хотя бы два исхода, неравноценных в системе предпочтений ЛПР (Лицо Принимающее Решения). Например, операция Q:(-2;10), означающая, что ЛПР может получить доход 10 или убыток -2, является рискованной. Операция H:(3;12) также является рискованной,
ибо даже получив доход 3, ЛПР будет недоволен - ведь мог бы получить 12 !
Однако количественно оценить риск возможно лишь если операция вероятностно
характеризуема, т.е. ее доход есть случайная величина (с.в.)- это предполагает возможность неоднократного повторения этой операции. Итак, пусть доход
от операции Q есть с.в., которую будем обозначать также как и саму операцию Q. Математическое ожидание M[Q] называют еще средним ожидаемым доходом,
а риск операции r отождествляют со средним квадратическим отклонением СКО,
т.е. квадратным корнем из дисперсии D[Q] . Задана с.в. дохода Q , находится
средний ожидаемый доход M[Q], дисперсия D[Q] и риск операции r. Вероятности
конкретных величин дохода - десятичные дроби с точкой вида 0.2 .
│ 33 │ 38 │ 42 │ 47 │ средний ожидаемый доход 41.40
Q: ├───────┼─────── дисперсия дохода 38.04
│ 0.3 │ 0.1 │ 0.1 │ 0.5 │ риск операции 6.17
Для уточнения распределения вероятностей можно провести пробную операцию.
После ее проведения вероятности могут стать совершенно иными и средний ожидаемый доход может значительно увеличиться. Если решение принимается по максимуму среднего ожидаемого дохода, то прибавка среднего ожидаемого дохода и есть максимальная стоимость пробной операции, при которой она еще оправдана
Найдём эту стоимость.
Первоначальные вероятности и характеристики операции
│ 33 │38 │ 42 │ 47 │ средний ожидаемый доход 41.40
Q: ├───────┼───────┼ дисперсия дохода 38.04
│ 0.30 │0.10│ 0.10 │0.50│ риск операции 6.17
Вероятности и характеристики операции после пробной операции
33 38 42 47 средний ожидаемый доход 45.60
Q: ├───────┼───────┼ дисперсия дохода 17.64
│ 0.10 │0.00│ 0.00 │0.90│ риск операции 4.20
4.2. Анализ по доходу и риску набора операций вероятностно характеризуемой
Задаём 4 операции по примеру (12,1/2)(3,1/2)(4,1/4)(10,1/4) т.е. в каждой
операции 4 возможных дохода - первое число в каждой паре скобок, второе число
в этой паре скобок - это вероятность этого дохода - какая-то правильная
дробь. Сумма всех вероятностей-дробей должна быть равна 1. Для каждой
операции подсчитаем средний ожидаемый доход m и среднее квадратическое отклонение - риск r. Каждая операция представляется в виде точки (r,m) на плоскость (риск - по горизонтали вправо, доход - по вертикали вверх) и выделено жирным шрифтом доминируемые операции и подчёркнутым - недоминируемые, т.е. оптимальные по Парето.
Доходы и вероятности средний ожидаемый
операций доход и риск операций
1-я операция (2,1/4)(6,1/4)(12,1/4)(20,1/4) 10.00 6.78
2-я операция (0,1/2)(4,1/4)(5,1/5)(20,1/20) 3.00 4.47
3-я операция (2,1/20)(6,1/4)(8,1/5)(22,1/2) 14.20 7.90
4-я операция (0,1/2)(4,1/4)(8,1/8)(32,1/8) 6.00 10.20
Нанесем средние ожидаемые доходы
и риски 
на плоскость – доход о
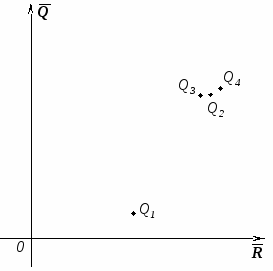ткладываем по вертикали, а риски по горизонтали (см. рис.):Получили 4 точки. Чем выше точка
, тем более доходная операция, чем точка правее – тем более она рисковая. Значит, нужно выбирать точку выше и левее. Точка 
доминирует точку , если Q΄ и r΄ и хотя бы одно из этих неравенств строгое. В нашем случае 3-я операция доминирует 2-ую, а 1-ую, 3-ю и 4-ую операции сравнивать нельзя, т.к. при переходе от первой операции к 4-ой с ростом риска растет доход. Легко видеть, что если из рассмотренных операций надо выбирать лучшую, то ее обязательно надо выбрать из операций по Парето.Пусть Q1 и Q2 две финансовые операции с эффективностями e1, e2 и рисками r1, r2 соответственно. Пусть t – какое-нибудь число между 0 и 1. Тогда операция Qt=(1-t)Q1+tQ2 называется линейной комбинацией операций Q1, Q2. При движении от 0 к 1 операция Qt изменяется от Q1 до Q2. Эффективность операции Qt равна (1-t)e1+te2, с риском же дело обстоит сложнее.
4.3.Риск линейных комбинаций двух некоррелированных операций
Пусть Q1 и Q2 две финансовые операции с эффективностями e1,e2 и
рисками r1,r2 соответственно. Пусть t - какое-нибудь число между 0 и 1 .
Тогда операция Qt=(1-t)Q1+tQ2 называется линейной комбинацией операций Q1,Q2.
При движении от 0 к 1 операция Qt изменяется от Q1 до Q2. Эффективность
операции Qt равна (1-t)e1+te2, с риском же дело обстоит сложнее. Рассмотрим
только случай некоррелированных операций Q1,Q2, тогда дисперсия операции
Qt равна (1-t)^2*D1+(t)^2*D2, где D1,D2 - дисперсии операций, значит,
риск операции Qt есть rt=Sqrt((1-t)^2*r1^2+(t)^2*r2^2). Зададим эффективности и риски операций Q1,Q2 и увидим кривую рисков-эффективностей линейных
комбинаций этих операций. Линейные комбинации заполняют весь отрезок между
точками-операциями выделенные жирным шрифтом, а кривая их характеристик (рисков-эффективностей) выделена точечными линиями. Выделена также операция (Q1+Q2)/2 -
"среднее арифметическое" операций Q1,Q2 и указаны ее характеристики, еще
выделена операция с наименьшим риском - она также разделяет точки - линейные
комбинации на оптимальные по Парето и нет. Обратим внимание, что эта операция
лучше одной из двух заданных операций - это есть эффект диверсификации в
двух операций в простейшей форме.
1-я операция 2-я операция
эффективность xx<=20 риск 30<=xx эффективность xx>=60 риск xx>=60
20 20 70 70
e
70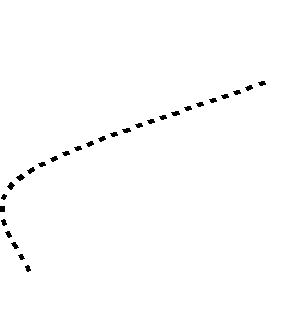
65Q3(70;70)60
5550
45
40
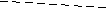35 Qp(35,20) -- Qs(33;40)30
25
20
15
10 Q2(20;20)
5
1
0 1 10 20 30 40 50 60 70 r4.4.Оптимисты, объективисты и пессимисты по отношению к риску
Вам предлагают купить лотерейный билет, по которому немедленно будет проведен
розыгрыш. У Вас равные шансы выиграть сумму S=$100 и остаться при своих
- ничего ни выиграть ни проиграть. За какую сумму Вы купили бы этот билет?
Если за $50, то Вы "объективист". Так называют тех, кто покупает билет за сум-
му M, равную математическому ожиданию выигрыша - в данном случае M=$50.
Если Вы согласны заплатить за билет лишь менее M , например, только $45, то
Вы не любите рисковать. Условно будем называть не любящих рисковать пессимис-
тами(они не верят в выигрыш).
Если же Вы согласны заплатить за билет более M , например, 55 долларов, то Вы
уверены, что Вам повезет и Вы выиграете $100. В этом случае Ваше отношение к
риску положительное. Вас можно назвать оптимистом - любящим риск (risk lover).
Это что касается покупной цены лотерейного билета. Но можно узнать о Вашем от-
ношении к риску, рассуждая так же о продажной цене лотерейного билета.
Фиксируем теперь сумму $100 и будем изменять вероятность выигрыша p . Рассма-
триваемый лотерейный билет при данном p дает выигрыш $100 с вероятностью p.
Графики цены такого билета для объективиста, пессимиста и оптимиста см. далее.
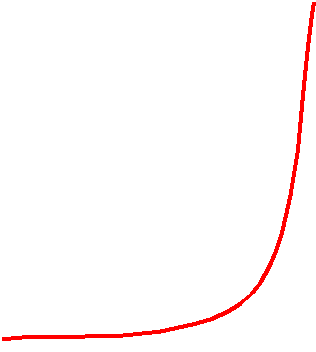
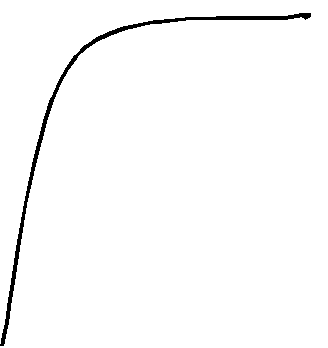
Рассмотрим плоскую фигуру, образованную ломаной OCM и прямой объективиста
или кривой оптимиста или пессимиста. Доля f, которую занимает эта фигура в
прямоугольнике OAMC оценивает отношение индивида к риску. Если f=0,5, то
это объективист, при f<0,5 - это пессимист, при f>0,5 - оптимист.
объективисты
А (0;100) М(1;100)
оптимисты
25.00
пессимисты Р
0 (0;0) 0,50 С (1;0)
Отношения к риску:
Для оптимистов: 0,33
Для объективистов: 0,55
Для пессимистов: 0,67
Налоговые шкалы
5.1.Расчет налога по налоговой шкале
Обозначим x месячный доход налогоплательщика, N(x) величину подоходного
налога или просто налог, R(x)- остаток дохода налогоплательщика, R(x)=x-N(x).
Аксиома подоходного налога АПН. Налог и остаток налога должны быть возрастающими функциями дохода, а остаток - строго возрастающей функцией дохода.
Распространенный способ задания подоходного налога - с помощью налоговой
шкалы. Налоговая шкала Т=(t0;a1,t1;...;ak,tk) - это (2k+1) чисел; k строго
возрастающих чисел a1,..,ak, называемых делениями шкалы, и (k+1) чисел t0,..,tk
из промежутка [0,1), называемых налоговыми ставками.
Налог N(x) определяется по шкале T следующим образом:
Ї t0*x, 0<=x<=a1,
│ t0*a1+t1*(x-a1), a1<=x<=a2,
N(x)= │ ....
└ t0*a1+t1*(a2-a1)+...+tk*(x-ak), x>ak.
Налоговая шкала называется прогрессивной, если налоговые ставки строго
возрастают, и регрессивной, если налоговые ставки строго убывают.
Найдите подоходный налог и остаток дохода при двух доходах x=32 и 47 при
налоговой шкале: (0.13;20,0.2;40,0.3;60,0.4) (например, все в тысячах руб.).
Нарисуем график налога и остатка дохода и укажем на графике значения налога
и остатка дохода при указанных выше значениях дохода. Определим, является ли
налоговая шкала прогрессивной или регрессивной.
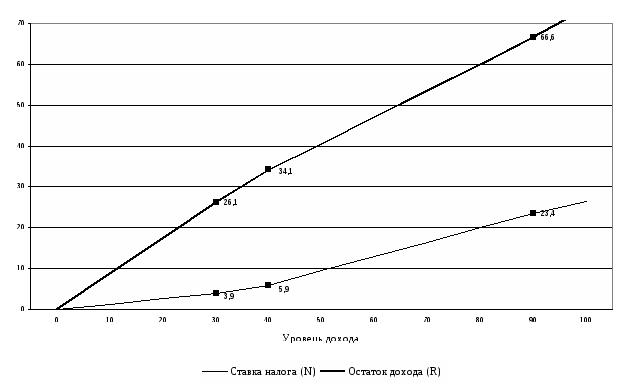
Задача 5.2. Средняя ставка налога
Существует более общий способ задания налога, чем с помощью налоговой шкалы.
Предварительное определение. Средней ставкой подоходного налога называется
произвольная непрерывная функция со значениями в промежутке [0,1).
Если y(x) - такая функция, то налог N(x) равен по определению y(x)*x,
следовательно, при известном налоге N(x) средняя ставка равна N(x)/x.
Если налог задан шкалой, то средняя ставка налога вычисляется по шкале так:
Ї (t0*x)/x, 0<=x<=a1,
│ (t0*a1+t1*(x-a1))/x, a1<=x<=a2,
y(x)= │ ....
└ (t0*a1+t1*(a2-a1)+...+tk*(x-ak))/x, x>ak.
Если выполнить почленное деление, то получим другое выражение средней
ставки через параметры шкалы (s1,s2 и т.д. - некоторые новые параметры шкалы:
Ї t0, 0<=x<=a1,
│ t1+s1/x, a1<=x<=a2,
y(x)= │ ....
└ tk*sk/x, x>ak.
Из АПН следует, что средняя ставка налога должна удовлетворять условию
y`(x)<(1-y(x))/x .
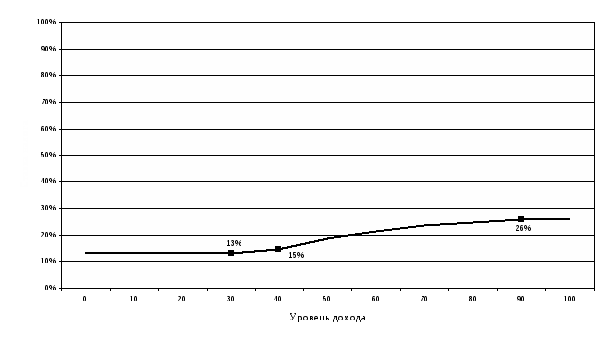
Напишем два выражения для средней ставки налога и начертим ее график при
налоговой шкале: (0.13;20,0.2;40,0.3;60,0.4) (например, все в тысячах руб.).
Найдём величину средней ставки налога при двух доходах x=32 и 47.
5.3.Виды подоходных налогов
Cуществуют различные виды подоходных налогов, которые отражены на практике.
Определение. Подоходный налог называется:
а)выпуклым, если N(x)-выпуклая функция и вогнутым, если N(x)-вогнутая функция;
б)прогрессивным, если средняя ставка N(x)/x - возрастающая функция
и регрессивным, если N(x)/x - убывающая функция;
в)пропорциональным, если N(x)/x=Const , т.е. если средняя ставка постоянна;
г)ультрааддитивным, если N(a)+N(b)<=N(a+b) для любых a,b; и инфраддитивным,
если N(a)+N(b)>=N(a+b).
Можно доказать, что указанные выше первые и вторые свойства связаны
следующими импликациями: a)->б)->г);в)->б);a)->в), причем стрелки необратимы,
т.е. выпуклость строго сильнее прогрессивности, прогрессивность строго
сильнее ультрааддитивности, пропорциональность строго сильнее прогрессивности
(тем самым существует прогрессивный, но не пропорциональный налог).
Также можно доказать, что для прогрессивной налоговой шкалы подоходный
налог выпуклый, а для регрессивной - вогнутый.
Для налоговой шкалы: (0.13;20,0.2;40,0.3;60,0.4) (например, все в тысячах
руб.) выясните, имеет ли заданный ею налог какое-либо свойство а-г) - см. выше.
6.Налоги на рынке с линейными функциями спроса и предложения
6.1.Параметры рынка с линейными функциями спроса и предложения
Рассматривается рынок одного товара. Пусть D(p) - функция спроса на товар,
она убывающая, S(p) - функция предложения товара, она возрастающая функция
цены. Если на рынке цена товара равна p, то количество денег, перешедшее от
покупателей к продавцам за единицу времени равно W(p)=p(мin{S(p),D(p)}).
Другой способ описания W(p): W(p)=pS(p) при p<=p* и W(p)=pD(p) при p>=p*.
Здесь p* - равновесная цена: при которой спрос равен предложению S(p)=D(p).
Если ни покупатели, ни продавцы не могут изменить цену, сложившуюся на рынке,
иначе как изменением суммарного спроса или предложения, то рынок называется
совершенным. Равновесное состояние рынка означает равенство спроса и
предложения; цена, при которой достигается это равенство называется равновесной
ценой, она есть решение уравнения S(p)=D(p). При выведении совершенного
рынка из равновесного состояния он переходит в другое равновесное состояние.
При линейных функциях спроса D(p)=c-dp и предложения S(p)=-a+bp, a,b,c,d>0,
равновесное состояние рынка существует если и только если (c/d)>(a/b) - это
условие далее предполагается. Сама равновесная цена равна p*=(a+c)/(b+d).
Для рынка одного товара с линейными функциями с параметрами
a=10,b=30,c=100,d=10; начертиv графики функций спроса и предложения,
найдём равновесную цену. Начертим график функции W(p) - суммы, переходящей от
покупателей к продавцам за единицу работы рынка, найти точку максимума этой
функции и сам максимум. Отметим, что если (c/2d)
и равен (p*)S(p*), иначе максимум при p=c/2d и равен (c/2d)D(c/2d).
р*=10+100/30+10=2,75
6.2.Налог с продаж
Рассматривается совершенный рынок одного товара. Пусть D(p), S(p) - линейные
функции спроса и предложения товара. Введем налог с продаж, его ставку
обозначим t . С выручки W за единицу работы продавцы платят налог tW. В
качестве аксиомы примем, что после введения налога с продаж функция спроса не
изменится: D(p)=D(p), функция же предложения станет такой S(p)=S((1-t)p) -
ведь без налога с продаж продавец, назначая цену p , рассчитывает получить
именно p с каждой единицы товара, а после введения налога с продаж он
получит в итоге только (1-t)p.
Новое равновесное состояние рынка (после введения налога) найдем, приравняв
функцию спроса и новую функцию предложения: D(p)=S(p), откуда получим новую
равновесную цену (pt)=(a+c)/(b(1-t)+d) - видим, что новая равновесная цена
больше прежней.
Налоговый орган хочет найти такую ставку t*, при которой взимаемый налог
с продаж максимален. Для этого надо найти максимум по t функции
N(t)=t(pt)(c-d(pt))=t(a+c)/(b(1-t)+d)[c-d(a+c)/(b(1-t)+d)]. Оказывается, что
t*=(bc-ad)/(b(c+dp*), соответствующая равновесная цена (pt*)=c/(2d)+p*/2 -здесь
p*=(a+c)/(b+d) - равновесная цена до введения налога с продаж. Налог с продаж,
уплачиваемый при ставке t* равен N*=t*(pt*)(c-d(pt*)).
Нарисуем графики функций спроса D(p)=100-10p и функций предложения
S(p)=-10+30p и S(p)=-10+30(1-t*)p). Подсчитаем оптимальную ставку
налога t*, налог по этой ставке и новую равновесную цену.
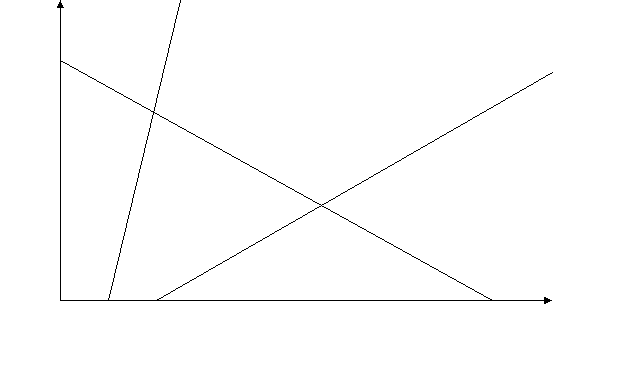
Оптимальная ставка налога:
t t*=(30*100-10*10)/(30(100+10*2,75)=0,76=76%
Новая равновесная цена:
(pt*)=100/(2*10)+2,75/2=6, 38
Налог по новой ставке:
N*=0,76*6,38*(100-10 *6,38)=224
6.3. Акцизный налог
Рассматривается совершенный рынок одного товара. Пусть D(p), S(p) - линейные
функции спроса и предложения товара. Введем акцизный налог, его ставку
обозначим t, т.е. за каждую проданную единицу товара продавцы платят налог t.
В качестве аксиомы примем, что после введения акцизного налога функция спроса
не изменится: D(p)=D(p), функция же предложения станет такой S(p)=S(p-t) -
ведь без акцизного налога продавец, назначая цену p , рассчитывает получить
именно p с каждой единицы товара, а после введения налога с продаж он
получит в итоге только (p-t).
Новое равновесное состояние рынка (после введения налога) найдем, приравняв
функцию спроса и новую функцию предложения: D(p)=S(p), откуда получим новую
равновесную цену (pt)=(a+c+bt)/(b+d) - видим, что новая равновесная цена
больше прежней.
Налоговый орган хочет найти такую ставку t*, при которой взимаемый акцизный
налог максимален. Для этого надо найти максимум по t функции
N(t)=t(pt)(c-d(pt))=t(a+c+bt)/(b+d)[c-d(a+c+bt)/(b+d)]. Оказывается, что
t*=(bc-ad)/(2bd), соответствующая равновесная цена (pt*)=c/(2d)+p*/2 - здесь
p*=(a+c)/(b+d) - равновесная цена до введения налога с продаж. Акцизный налог,
уплачиваемый при ставке t* равен N*=t*(pt*)(c-d(pt*)).
Нарисуем графики функции спроса D(p)=100-10p и функций предложения
S(p)=-10+30p и S(p)=-10+30((1-t*)p). Подсчитаем оптимальную ставку
налога t*, акцизный налог по этой ставке и новую равновесную цену.
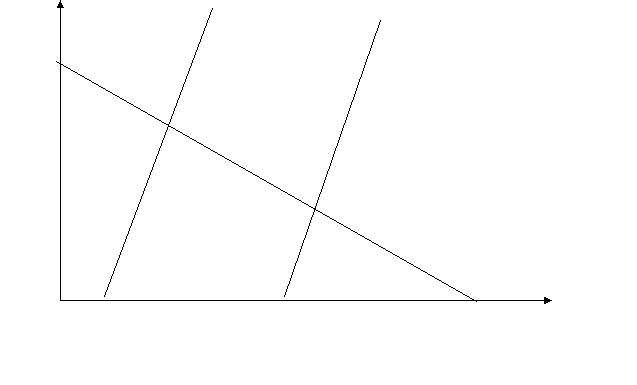
Оптимальная ставка налога:
t*=30*100-10*10/2*30*10=4,8
Новая равновесная цена:
(pt*)=100/(2*10)+2,75/2=6, 38
Налог по новой ставке:
N*=4,8*6,38*(100-10 *6,38)=1415
Налоги в теории фирмы
7.1. Налог на прибыль
Теория фирмы. В общем случае деятельность фирмы описывается производственной
функцией f, которая устанавливает связь между вектором-столбцом использованных ресурсов X и величиной y выпускаемой продукции. Пусть w - цена этой
продукции, P - вектор-строка) цен на ресурсы, тогда wf(X)-PX, т.е. выручка
минус затраты есть прибыль фирмы и обозначается F(X). Известно, что
состояние равновесия фирмы (в смысле оптимальности ее размера) характеризуется
условием wf`(X)=P, где f`(X) есть вектор-строка частных производных f.
Рассмотрим частный случай. Пусть цена продукции фирмы w линейно падает с
ростом объема поставки y на рынок: w(y)=a-by, себестоимость единицы продукции
постояннa и равна c , так что издержки производства выражаются формулой:
C(y)=cy+d; a,b,c,d>0; (константа d имеет смысл расходов на поддержание
нулевого уровня производства - такие расходы всегда есть, хотя бы, например,
на зарплату сторожей).
Прибыль фирмы равна P(y)=yw(y)-C(y)=y(a-by)-(cy+d)=-by^2+(a-c)y-d. Пусть
ставка налога на прибыль равна z, тогда налог равен zP(y), остаток дохода
равен (1-z)P(y). При любой ставке налога z условие равновесия фирмы одно и
то же: P`(y)=0, максимизирующий прибыль объем производства равен y*=(a-c)/2b,
сама максимальная прибыль фирмы равна (a-c)^2/(4b)-d, цена продукции при таком
объеме производства равна a-by*.
При конкретных данных a=100, b=10, c=14, d=10 и налоговой ставке z=0.24 начертим графики прибыли P(y), налога N, остатка налога R и найдём указанные характеристики.
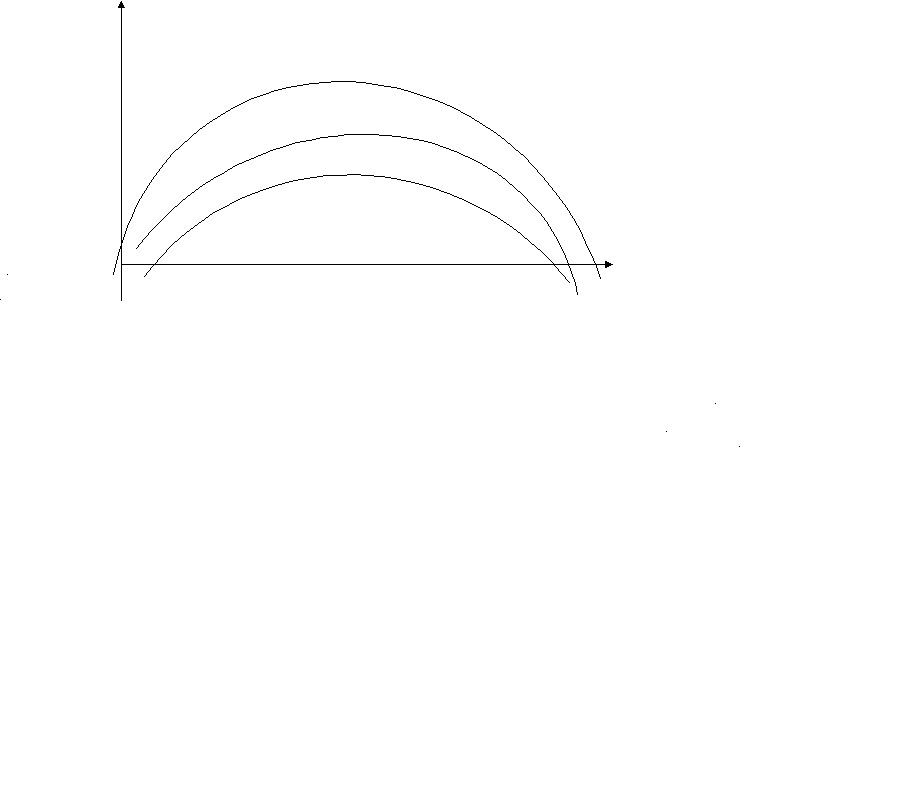
Оптимальный объем производства:
y*=(100-14)/2*10=4,3
Цена продукции при таком производстве:
р=100-4,3*10=57
Максимальная прибыль:
Р=(100-14)²/(4*10)-10=246,5
Максимальная сумма налога:
N=246,5*0,24=59,16
Максимальный остаток дохода:
R=246,5-59,16=187,34
7.2.Акцизный налог
Пусть теперь фирма выплачивает акцизный налог (и только его) по ставке t, так
что при объеме производства y доход фирмы будет уже I(y,t)=y(a-by)-(cy+d)-ty.
Для нахождения оптимального объема производства yt при ставке налога t найдем
производную функции I(y,t) по y и приравняем ее нулю, получим yt=(a-c-t)/2b.
Налоговый орган выберет ставку t*, максимизирующую налог G(y)=ty. Имеем
G(yt)=t(a-c-t)/2b. Функция G от t есть парабола, у ней ветви направлены
вниз, а корни есть 0 и (a-с), так что максимум ее достигается при t*=(a-c)/2.
При этой ставке акцизного налога объем производства равен (a-c)/4b, сам
максимум равен (a-c)²/8b, доход фирмы равен (a-c)²/(16b)-d, и видно что
доход равен половине выплачиваемого налога минус константа d.
Перепишем доход фирмы после уплаты акцизного налога
I(y,t)=y(a-by)-(cy+d)-ty=-b[y-(a-c-t)/(2b)]²+(a-c-t)²/(4b)-d.
При оптимальном для этой ставки налога объеме производства yt=(a-c-t)/2b
получим I(yt,t)=(a-c-t)²/(4b)-d. Видно, что при приближении t к (a-c) доход
фирмы становится нулевым, именно, при t=(a-c-√(4bd)), а потом и
отрицательным. Следовательно, после перехода ставки налога через критическое
значение t объем производства станет нулевым - фирма перестанет работать или
уйдет в "теневую экономику". График функции G c таким комментарием известен
как кривая Лаффера.
При конкретных данных a=100, b=10, c=14, d=10 начертим кривую Лаффера
и найдём указанные характеристики.
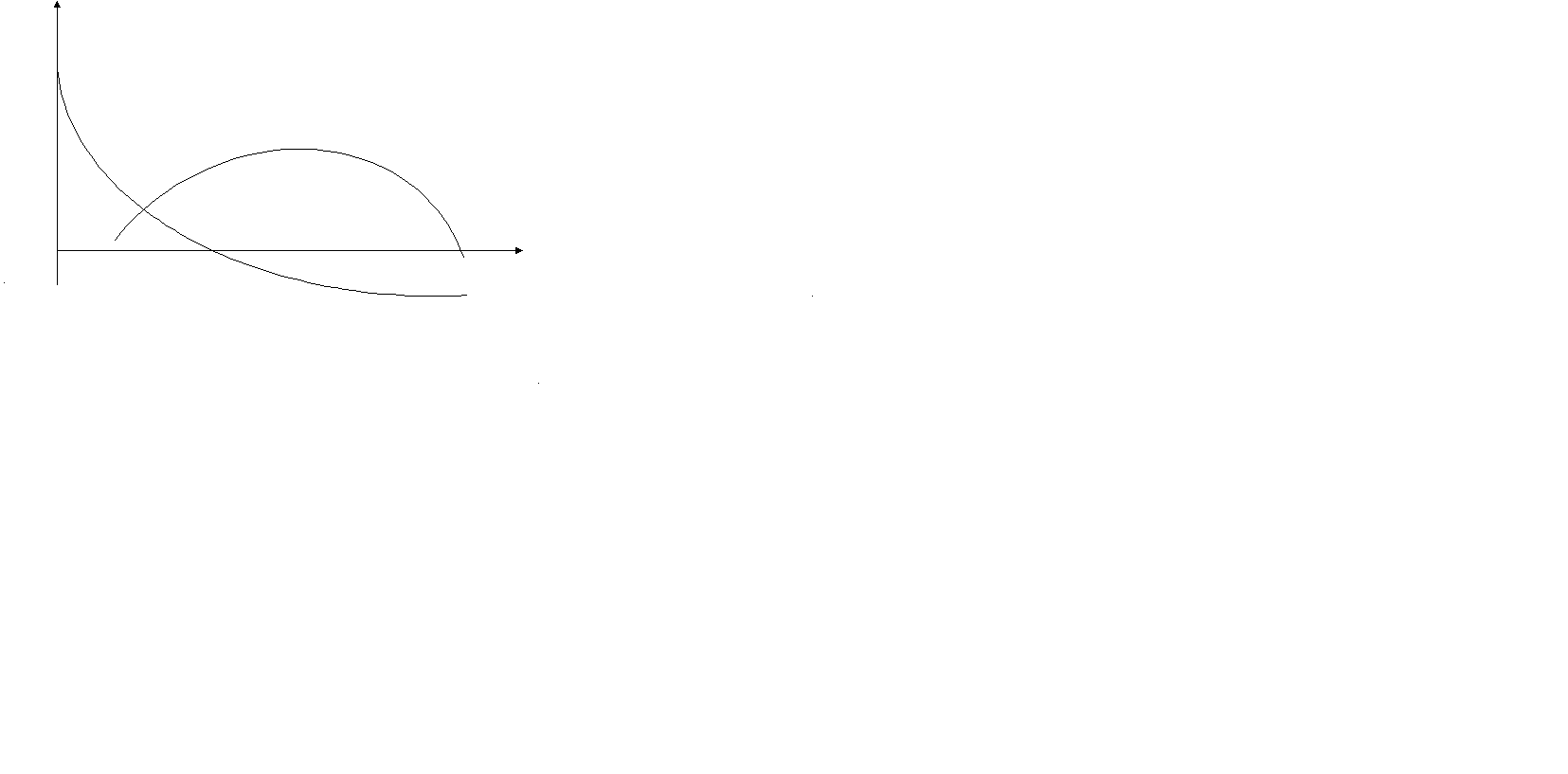
Оптимальная ставка акцизного налога:
t*=100-14/2=43
Максимальная сумма налога:
G=43*(100-14-43)/2*10=92,45
Критическая ставка налога:
t=100-14-√4*10*10=66
Статистический анализ денежных потоков
8.1.Статистический анализ денежных потоков
Исходные данные для анализа: ежедневные (суммарные) денежные вклады населения,
в отделение сбербанка в течение 4- недель (или аналогичный какой-нибудь денеж-
ный поток). Для удобства обработки все числа предполагаются целыми и не более
чем двузначными, что всегда можно сделать округлением и масштабированием.
Данная программа не предназначена для обработки реальных данных, она имеет
исключительно демонстрационный характер.
1-я неделя 2-я неделя 3-я неделя 4-я неделя
---------------- ---------------- ---------------- ----------------
1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6
15 8 8 8 8 8 │ 8 11 11 11 11 11 │ 11 0 2 18 16 6 │ 5 4 6 15 14 13
Объем выборки n = 24. Составим ранжированный ряд денежных потоков:
20,22,24,25,26,26 28,28,28,28,28,28 31,31,31,31,31,31 33,34,35,35,36,38
Составим дискретный вариационный ряд
| xi | 20 | 22 | 24 | 25 | 26 | 28 | 31 | 33 | 34 | 35 | 36 | 38 |
| pi | 1/24 | 1/24 | 1/24 | 1/24 | 2/24 | 6/24 | 6/24 | 1/24 | 1/24 | 2/24 | 1/24 | 1/24 |
Построим многоугольник частостей:
xi—1/2
—
1/4
│ │ │ │1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 pi
Построим график выборочной функции распределения:
1
│ │ │