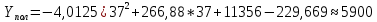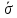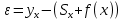 (3.8) (3.8)
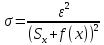 (3.9) (3.9)
Полученные результаты сведем в таблицы 3.9 и 3.10.
Таблица 3.9 – Значения ошибки построенный моделей
Месяц
|
Ошибка модели
|
Экспоненциальной
|
Линейной
|
Логарифмической
|
Полиномиальной
|
Степенной
|
Гиперболической
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
Январь
|
-1705,113
|
-1683,137
|
-269,952
|
-961,198
|
-460,317
|
532,077
|
Февраль
|
-93,878
|
-83,137
|
706,295
|
542,502
|
648,772
|
214,734
|
Март
|
-295,215
|
-295,804
|
148,572
|
233,535
|
151,005
|
-629,628
|
Апрель
|
1013,208
|
1001,196
|
1213,087
|
1434,235
|
1250,113
|
356,151
|
Май
|
824,394
|
800,863
|
840,974
|
1137,602
|
900,371
|
-27,798
|
Июнь
|
-198,658
|
-233,804
|
-327,748
|
6,635
|
-252,889
|
-1182,663
|
Июль
|
-399,946
|
-446,804
|
-649,256
|
-302,665
|
-563,236
|
-1479,889
|
Август
|
-720,137
|
-778,804
|
-1071,426
|
-730,965
|
-977,105
|
-1873,823
|
Сентябрь
|
-199,896
|
-270,471
|
-639,535
|
-318,932
|
-538,905
|
-1412,701
|
Октябрь
|
1049,778
|
967,196
|
532,301
|
822,435
|
637,800
|
-212,043
|
Ноябрь
|
669,551
|
574,863
|
82,549
|
333,802
|
191,847
|
-634,045
|
Декабрь
|
-272,241
|
-379,137
|
-922,064
|
-716,498
|
-809,778
|
-1612,271
|
Январь
|
-154,712
|
-251,057
|
-1187,428
|
-636,658
|
-981,790
|
-1962,095
|
Февраль
|
-916,333
|
-1013,057
|
-1663,193
|
-1398,658
|
-1522,578
|
-1776,882
|
Март
|
-865,617
|
-962,724
|
-1463,302
|
-1348,325
|
-1351,545
|
-1420,367
|
Апрель
|
451,768
|
354,276
|
-50,766
|
-31,325
|
44,590
|
44,007
|
Май
|
-800,176
|
-898,057
|
-1235,976
|
-1283,658
|
-1151,093
|
-1123,601
|
Июнь
|
-1264,451
|
-1362,724
|
-1650,709
|
-1748,325
|
-1572,992
|
-1534,304
|
Июль
|
-93,056
|
-191,724
|
-441,094
|
-577,325
|
-368,515
|
-326,545
|
Август
|
1209,342
|
1110,276
|
891,626
|
724,675
|
960,396
|
1001,719
|
Продолжение таблицы 3.9
1
|
2
|
3
|
4
|
5
|
6
|
7
|
Сентябрь
|
478,077
|
378,609
|
184,937
|
-6,992
|
250,811
|
289,505
|
Октябрь
|
1466,149
|
1366,276
|
1193,269
|
980,675
|
1256,895
|
1291,988
|
Ноябрь
|
1315,224
|
1214,943
|
1059,278
|
829,342
|
1121,133
|
1152,199
|
Декабрь
|
1191,636
|
1090,943
|
950,009
|
705,342
|
1010,448
|
1037,363
|
Январь
|
2012,270
|
1934,023
|
1457,300
|
1596,482
|
1607,589
|
1430,018
|
Февраль
|
1162,656
|
1096,023
|
956,819
|
854,782
|
1039,288
|
1562,148
|
Март
|
1313,278
|
1258,356
|
1314,651
|
1113,415
|
1366,023
|
2049,996
|
Апрель
|
-1312,531
|
-1355,644
|
-1162,401
|
-1404,285
|
-1129,221
|
-400,157
|
Май
|
128,228
|
97,023
|
394,923
|
144,682
|
416,204
|
1151,399
|
Июнь
|
1615,555
|
1596,356
|
1978,378
|
1740,315
|
1991,363
|
2716,968
|
Июль
|
645,448
|
638,356
|
1090,271
|
878,615
|
1097,232
|
1806,436
|
Август
|
-336,759
|
-331,644
|
179,721
|
4,915
|
182,191
|
872,105
|
Сентябрь
|
-125,735
|
-108,311
|
454,519
|
324,548
|
453,577
|
1123,197
|
Октябрь
|
-2363,481
|
-2333,644
|
-1725,649
|
-1804,485
|
-1729,212
|
-1079,944
|
Ноябрь
|
-1832,329
|
-1789,977
|
-1141,907
|
-1164,518
|
-1147,498
|
-518,153
|
Декабрь
|
-766,949
|
-711,977
|
-28,024
|
9,782
|
-35,188
|
574,908
|
Таблица 3.10 – Среднеквадратические отклонения моделей
Месяц
|
СКО модели
|
Экспоненциальной
|
Линейной
|
Логарифмической
|
Полиномиальной
|
Степенной
|
Гиперболической
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
Январь
|
0,019750
|
0,019314
|
0,000637
|
0,007123
|
0,001787
|
0,002891
|
Февраль
|
0,000052
|
0,000041
|
0,003376
|
0,001939
|
0,002821
|
0,000288
|
Март
|
0,000622
|
0,000625
|
0,000170
|
0,000427
|
0,000176
|
0,002677
|
Апрель
|
0,006799
|
0,006626
|
0,010071
|
0,014607
|
0,010761
|
0,000757
|
Май
|
0,003378
|
0,003177
|
0,003523
|
0,006726
|
0,004073
|
0,000003
|
Июнь
|
0,000212
|
0,000292
|
0,000567
|
0,000000
|
0,000341
|
0,006542
|
Июль
|
0,000927
|
0,001149
|
0,002353
|
0,000539
|
0,001794
|
0,010837
|
Август
|
0,002695
|
0,003125
|
0,005674
|
0,002772
|
0,004782
|
0,015550
|
Сентябрь
|
0,000219
|
0,000396
|
0,002099
|
0,000547
|
0,001512
|
0,009193
|
Октябрь
|
0,008255
|
0,006908
|
0,001944
|
0,004873
|
0,002841
|
0,000274
|
Ноябрь
|
0,002359
|
0,001715
|
0,000033
|
0,000559
|
0,000181
|
0,001765
|
Декабрь
|
0,000414
|
0,000790
|
0,004317
|
0,002685
|
0,003383
|
0,011990
|
Январь
|
0,000133
|
0,000344
|
0,006736
|
0,002093
|
0,004738
|
0,016569
|
Февраль
|
0,004123
|
0,004972
|
0,012266
|
0,008988
|
0,010475
|
0,013791
|
Март
|
0,004327
|
0,005275
|
0,011315
|
0,009770
|
0,009812
|
0,010728
|
Продолжение таблицы 3.10
1
|
2
|
3
|
4
|
5
|
6
|
7
|
Апрель
|
0,001100
|
0,000667
|
0,000013
|
0,000005
|
0,000010
|
0,000010
|
Май
|
0,002654
|
0,003302
|
0,005992
|
0,006425
|
0,005253
|
0,005022
|
Июнь
|
0,007110
|
0,008151
|
0,011517
|
0,012757
|
0,010564
|
0,010102
|
Июль
|
0,000041
|
0,000172
|
0,000882
|
0,001483
|
0,000622
|
0,000491
|
Август
|
0,006286
|
0,005230
|
0,003279
|
0,002120
|
0,003838
|
0,004198
|
Сентябрь
|
0,001028
|
0,000636
|
0,000148
|
0,000000
|
0,000274
|
0,000368
|
Октябрь
|
0,012802
|
0,010948
|
0,008134
|
0,005322
|
0,009112
|
0,009680
|
Ноябрь
|
0,007485
|
0,006304
|
0,004696
|
0,002795
|
0,005303
|
0,005623
|
Декабрь
|
0,006473
|
0,005352
|
0,003983
|
0,002126
|
0,004542
|
0,004805
|
Январь
|
0,018301
|
0,016729
|
0,008920
|
0,010901
|
0,011070
|
0,008559
|
Февраль
|
0,005469
|
0,004819
|
0,003609
|
0,002844
|
0,004302
|
0,010395
|
Март
|
0,008067
|
0,007351
|
0,008085
|
0,005643
|
0,008791
|
0,021798
|
Апрель
|
0,007557
|
0,008016
|
0,006047
|
0,008546
|
0,005732
|
0,000796
|
Май
|
0,000057
|
0,000032
|
0,000556
|
0,000072
|
0,000619
|
0,005181
|
Июнь
|
0,009592
|
0,009344
|
0,015039
|
0,011301
|
0,015261
|
0,031150
|
Июль
|
0,001624
|
0,001587
|
0,004902
|
0,003098
|
0,004969
|
0,014785
|
Август
|
0,000403
|
0,000391
|
0,000122
|
0,000000
|
0,000126
|
0,003137
|
Сентябрь
|
0,000058
|
0,000043
|
0,000820
|
0,000411
|
0,000817
|
0,005459
|
Октябрь
|
0,026538
|
0,025978
|
0,015478
|
0,016734
|
0,015534
|
0,006668
|
Ноябрь
|
0,011945
|
0,011457
|
0,005046
|
0,005233
|
0,005092
|
0,001125
|
Декабрь
|
0,002190
|
0,001900
|
0,000003
|
0,000000
|
0,000005
|
0,001460
|
Рассчитаем средние значения СКО для каждой модели и внесем значения в таблицу 3.11, затем рассчитаем точность модели по формуле (3.10) и занесем в таблицу 3.11.
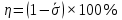 (3.10) (3.10)
Таблица 3.11 – Точность рассчитанных моделей
Модель
|
Экспоненциальная
|
Линейная
|
Логарифмическая
|
Полиномиальная
|
Степенная
|
Гиперболическая
|
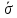
|
0,005
|
0,005
|
0,005
|
0,004
|
0,005
|
0,007
|
Точность модели, %
|
99,469
|
99,491
|
99,521
|
99,551
|
99,524
|
99,293
|
Таким образом, модель с полиномиальной функцией тренда является наиболее точной, следовательно, прогноз, сделанный на основании данных этой модели, будет достоверным (рисунок 3.2). Тогда полное уравнение для прогноза:
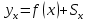 (3.11) (3.11)
Рассчитаем прогноз для 37-го месяца:
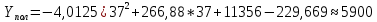
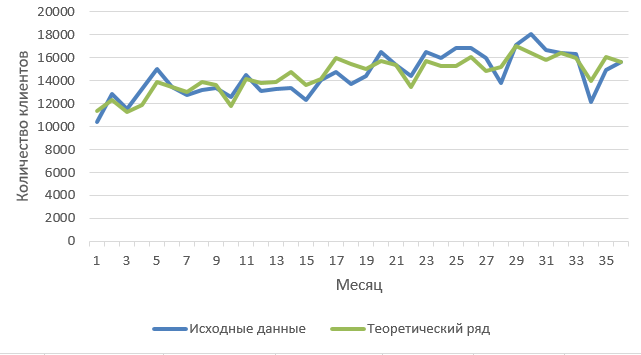
Рисунок 3.2 – Фактические и рассчитанные значения
Таким образом, имея набор статистических данных, методом аналитического выравнивания можно спрогнозировать данные на последующие несколько моментов времени. Но уровень их точности будет уменьшаться с увеличением дальности прогноза. Тем не менее, можно предугадать c точностью 98% количество клиентов для следующего месяца.
Заключение
Целью курсового проекта являлась организация Call-центра для оператора связи. Для достижения данной цели были выполнены следующие задачи:
изучен теоретический материал по организации, работе Call-центра и его показатели эффективности;
выбрана модель для расчета количества операторов Call-центра;
рассчитан прогноз числа клиентов на следующий месяц.
Для успешной работы Сall-центра количество работников должно быть таким, чтобы были обработаны все вызовы. Занятость оператора, равная 81% может считаться оптимальной. Такому уровню занятости соответствует число операторов равное 77.
При наличии набора статистических данных методом аналитического выравнивания были спрогнозированы данные на последующий месяц. Уровень их точности будет уменьшаться с увеличением дальности прогноза.
Для прогнозирования была выбрана полиномиальная зависимость, так как её точность составила 99,55%. Количество клиентов на 37-й месяц составило 5900.
Литература
Афанасьев В.Н., Юзбашев М.М. Анализ временных рядов и прогно-зирование: Учебник.- М.:Финансы и статистика, 2001 – 228 с.
Дуброва Т.А. Статистические методы прогнозирования: Учеб. посо-бие для вузов. - М.: ЮНИТИ-ДАНА, 2003. - 206с.
Елисеева И.И. Общая теория статистики: Учебник для вузов / И.И. Елисеева, М.М. Юзбашев; Под ред. И.И. Елисеевой. 4-е изд., перераб. и доп. М.: Финансы и статистика, 2002. 480 с.
Call-центр назначение, типы и задачи [Электронный ресурс] // TADVISER Государство. Бизнес. ИТ. URL: https://www.tadviser.ru/index.php/%D0%A1%D1%82%D0%B0%D1%82%D1%8C%D1%8F:Call-%D1%86%D0%B5%D0%BD%D1%82%D1%80_%D0%BD%D0%B0%D0%B7%D0%BD%D0%B0%D1%87%D0%B5%D0%BD%D0%B8%D0%B5,_%D1%82%D0%B8%D0%BF%D1%8B_%D0%B8_%D0%B7%D0%B0%D0%B4%D0%B0%D1%87%D0%B8#.D0.9E.D1.80.D0.B3.D0.B0.D0.BD.D0.B8.D0.B7.D0.B0.D1.86.D0.B8.D1.8F_.D1.80.D0.B0.D0.B1.D0.BE.D1.82.D1.8B (дата обращения: 24.11.2020).
Задачи Call-центра [Электронный ресурс] // CALLonline URL: http://www.callonline.ru/call/functions/ (дата обращения 24.11.2020).
Колл-центр [Электронный ресурс] // Calltouch URL: http://www.callonline.ru/call/functions/ (дата обращения: 24.11.2020).
Показатели эффективности работы колл-центра [Электронный ресурс] // MIGHTYCALL URL: https://www.mightycall.ru/blog/pokazateli-raboty-call-centra/ (дата обращения: 24.11.2020).
Что включено в функционал call центра [Электронный ресурс] // IP ATC Asteriks URL: http://www.call-center.su/faq/funktsional-call-centra.php (дата обращения: 24.11.2020).
 |
 Скачать 290.47 Kb.
Скачать 290.47 Kb.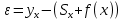 (3.8)
(3.8) 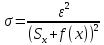 (3.9)
(3.9)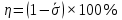 (3.10)
(3.10)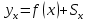 (3.11)
(3.11)