Курсовая работа по дисциплине Теория телетрафика Вариант 4 студент фаэс, гр. Аб85 М. А. Кравченко
 Скачать 290.47 Kb. Скачать 290.47 Kb.
|
2.2 Анализ характера закона распределения промежутков между моментами поступления заявокДля оценки характера закона распределения входящего потока необходимо провести измерение длительностей промежутков между поступлениями заявок. Для проведения анализа из генеральной совокупности производится выборка по следующему алгоритму: зафиксировать промежуток времени наблюдения, который задает объем выборки и обеспечивает условие, что поступающий поток сигнальных единиц близок к стационарному; зафиксировать число операторов; исследовать проводится отдельно для каждого оператора в течение фиксированного промежутка времени. Для сформированной выборочной совокупности определены длительности промежутков между поступлениями сигнальных единиц и рассчитаны: среднее значение, несмещенная оценка дисперсии и среднеквадратическое отклонение случайной величины. Кроме того, выполнен расчет коэффициента асимметрии β, характеризующего скошенность распределения по отношению к математическому ожиданию. [2] Для доказательства предположения соответствия распределения выборочной совокупности теоретическому распределению воспользуемся критерием согласия 2 Пирсона. При анализе характера закона распределения промежутков между поступлениями заявок будем использовать статистические данные о работе Call-центра (рисунок 2.1). 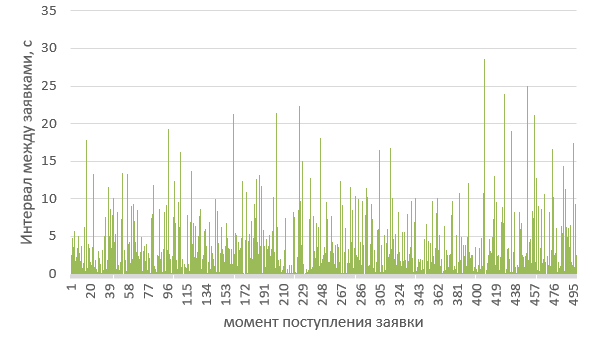 Рисунок 2.1 – Фрагмент исходной зависимости интервалов между поступлениями запросов от момента поступления Для выбранного периода наблюдений рассчитаем статистические характеристики, такие как средняя длительность интервалов между поступлениями сообщений, стандартное отклонение и асимметрия (таблица 2.1). При достаточно близком совпадении среднего значения и среднеквадратического отклонения случайной величины (коэффициент вариации  ) можно говорить о приемлемости гипотезы о показательном законе распределения промежутков между поступлениями сигнальных сообщений. Однако, такие проверки никак не могут доказать соответствия выборки теоретическому закону. [3] ) можно говорить о приемлемости гипотезы о показательном законе распределения промежутков между поступлениями сигнальных сообщений. Однако, такие проверки никак не могут доказать соответствия выборки теоретическому закону. [3]Для оценки степени зависимости случайных величин в последовательности интервалов времени между поступлениями заявок построены графики корреляционной функции. В таблице 2.1 приведены статистические характеристики выборки. Таблица 2.1 - Статистические характеристики выборки
Так как коэффициент вариации равен единице, то можно сделать первоначальное предположение, что поток запросов, поступающих на Call-центр, является простейшим. С помощью критерия серий, основанного на медиане выборки, докажем стационарность процесса. Таблица 2.2 – Результаты анализа критерия серий
Выполняются следующие неравенства: 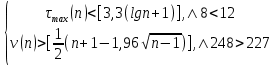 (2.1) (2.1)Делаем вывод, что процесс является независимым и стационарным. Для приемлемости гипотезы о показательном законе распределения необходимо определить степени зависимости случайных величин в последовательности интервалов времени между поступлениями заявок. [3] Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока: 0.1 < rt,t-1< 0.3: слабая; 0.3 < rt,t-1< 0.5: умеренная; 0.5 < rt,t-1< 0.7: заметная; 0.7 < rt,t-1< 0.9: высокая; 0.9 < rt,t-1< 1: весьма высокая. Коррелограмма исходного ряда, показанная на рисунке 2.2, получена с помощью программного пакета Excel. Она показывает незначительную зависимость, следовательно, гипотеза приемлема. 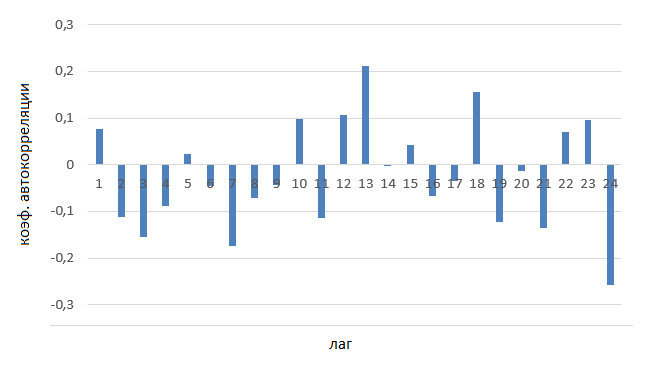 Рисунок 2.2 – Вычисленная коррелограмма исходного ряда Проведем подбор стандартного распределения вероятностей для аппроксимации распределения вероятностей интервалов между заявок Использование системы массового обслуживания (СМО), в которой учитывается характер распределения интервалов времени между поступлениями сообщений, позволяет получить более точные оценки таких параметров, как время ожидания клиента в очереди и область допустимых значений нагрузки, при которых обеспечивается требуемое качество обслуживания, чем получаемые при использовании Марковских моделей. Сравнение результатов экспериментальных исследований и теоретического расчета позволит уточнить закон распределения входящих запросов, влияющий на качество обслуживания. [1] Рассчитаем количество интервалов разбиения k по следующей формуле: k = 1 + 3.322lg(n) (2.2) Определим величину интервала группировки по следующей формуле: 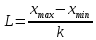 (2.3) (2.3)Для дальнейшего расчета будут браться значения L = 2.86, xmax = 28.62, xmin = 0, k = 10. Таблица 2.3 – Формирование сгруппированного ряда
Таким образом, статистический ряд представляется в виде гистограммы (рисунок 2.3). 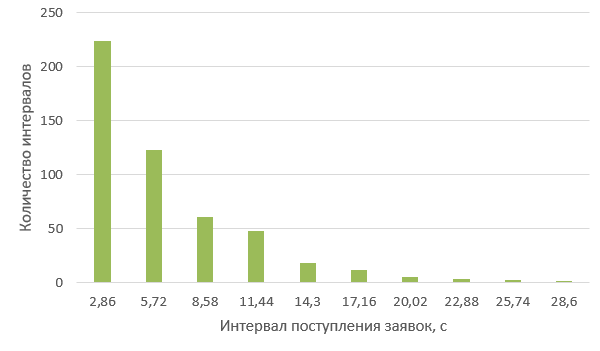 Рисунок 2.3 – Гистограмма интервалов между поступлением заявок В качестве оценки параметра λ показательного распределения величину, обратную выборочной средней: 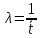 (2.4) (2.4)Значение выборочной средней возьмем из таблицы 2.1. 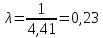 Рассчитаем теоретические частоты 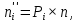 (2.5) (2.5)где Pi = e-λxi - e-λxi+1 – вероятности попадания случайной величины в частичные интервалы. [3] Далее сравним эмпирические и теоретические частоты с помощью критерия Пирсона (формула 2.6), приняв число степеней свободы k = s-2, где s – число первоначальных интервалов выборки. 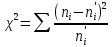 (2.6) (2.6)Таблица 2.4 – Расчет критерия Пирсона
По таблице критических точек распределения 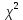 , по заданному уровню значимости α = 0,05 и числу степеней свободы k = 10–2 = 8 находим критическую точку правосторонней критической области , по заданному уровню значимости α = 0,05 и числу степеней свободы k = 10–2 = 8 находим критическую точку правосторонней критической области 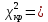 15,5. 15,5.Так как 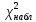 < < 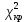 — нет оснований отвергнуть гипотезу о распределении выборки по показательному закону. Другими словами, данные наблюдений согласуются с этой гипотезой. — нет оснований отвергнуть гипотезу о распределении выборки по показательному закону. Другими словами, данные наблюдений согласуются с этой гипотезой. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

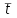 , с
, с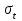 , с
, с