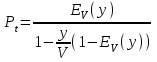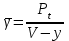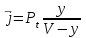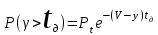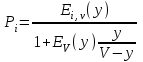Курсовая работа по дисциплине Теория телетрафика Вариант 4 студент фаэс, гр. Аб85 М. А. Кравченко

• Название: Курсовая работа по дисциплине Теория телетрафика Вариант 4 студент фаэс, гр. Аб85 М. А. Кравченко
• Дата: 05.12.2021
• Размер: 290.47 Kb.
• Имя файла: TT_Kravchenko_Maxim.docx
• Тип: Курсовая; #291845
• страница: 4 из 6

2.3 Расчет вероятностных характеристик

Вызовы (рисунок 2.4) поступают на систему по входящим соединительным линиям и обрабатываются операторами, число которых меньше либо равно числу линий. В случае, если входящий вызов застает все линии занятыми, то он отклоняется, абоненту телефонной сети будет передан сигнал “занято”. Если свободные линии есть, то вызов поступает в систему, далее в зависимости от числа свободных операторов вызов может быть немедленно передан на обслуживание либо поставлен на ожидание. [1]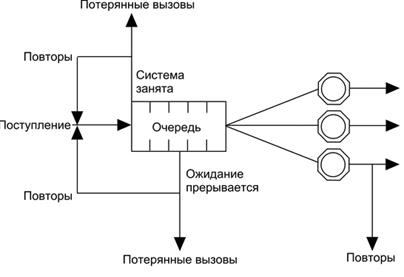


Рисунок 2.4 – Модель Call-центра
Часть вызовов может уйти из очереди, не дождавшись обслуживания. Для всех неуспешных (не окончившихся обслуживанием) вызовов возможны повторные попытки. Обслуженные вызовы могут уйти из системы или возвратиться в нее для дальнейшего обслуживания. Наиболее простым способом моделирования Call-центра является применение модели СМО типа M/M/v по классификации Кендалла, с неограниченным числом мест для ожидания.

Вторая формула Эрланга позволяет вычислить количество операторов, которые должны работать в Сall-центре, в зависимости от количества входящих звонков, обрабатываемых в Сall-центре за час, средней продолжительности звонка, а также допускаемой средней задержке при ответе на звонок.

Число операторов — важный параметр при планировании работы Сall-центра. Если операторов недостаточно, абонентам приходится подолгу ждать ответа на звонок, — следовательно, вы рискуете потерять часть клиентов. Если операторов слишком много, ценные ресурсы тратятся впустую.

Доля вызовов, задержанных при обслуживании, но не потерянных (вероятность того, что поступивший вызов не будет немедленно обслужен, а будет ожидать начала обслуживания в течение времени больше нуля) рассчитывается следующим образом:

(2.7)

Среднее время ожидания начала обслуживания (математическое ожидание начала обслуживания):

(2.8)

Среднее число вызовов, находящихся на ожидании

(2.9)

Вероятность того, что для поступившего в произвольный момент времени вызова ожидание будет больше t, определяется по формуле:

(2.10)

Изначально задаемся уровнем обслуживания, характеризуемым двумя базовыми числовыми параметрами, означающими, что время ожидания не должно превысить 10 с.

Средняя занятость оператора (или коэффициент использования) это соотношение, которое отражает количество времени, которое оператор потратил на ответ на звонки по сравнению с общим количеством рабочего времени (что может включать периоды отдыха операторов). Занятость операторов можно легко вычислить, разделив интенсивность трафика, выраженное в Эрл на количество операторов.

Вероятность того, что поступающие запросы немедленно обслуживаются:

(2.11)

Зная время обработки одного вызова 𝑡 = 270 с, рассчитаем нагрузку 𝑦 по формуле:
𝑦 = 𝜆∗𝑡 = 0,23∗270 = 62,1 ≈ 62 Эрл (2.12)
Занятость операторов рассчитывается по формуле: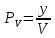
, (2.13)
где 𝑉− число операторов.

Из (2.13) следует, что при числе операторов равном нагрузке, занятость операторов будет 100%. Поэтому следует брать на рассмотрение количество операторов, начиная с 63 (V > y). Возьмем для расчетов диапазон из 18 значений количества операторов. Результаты расчета сведем в таблицу 2.5.


Таблица 2.5 – Определение оптимального количества операторов

Количество операторов	Вероятность соединения с оператором без постановки в очередь	Среднее время ожидания, сек	Средняя длина очереди	Уровень обслуживания	Занятость операторов
63	0,144	154,018	53,051	0,191	0,98
64	0,273	65,474	22,552	0,349	0,97
65	0,384	36,974	12,736	0,478	0,95
66	0,483	23,281	8,019	0,586	0,94
67	0,571	15,428	5,314	0,675	0,93
68	0,647	10,601	3,651	0,747	0,91
69	0,709	7,486	2,579	0,803	0,90
70	0,765	5,298	1,825	0,849	0,89
71	0,809	3,814	1,314	0,884	0,87
72	0,844	2,805	0,966	0,911	0,86
73	0,881	1,952	0,672	0,935	0,85
74	0,904	1,446	0,498	0,951	0,84
75	0,924	1,048	0,361	0,963	0,83
76	0,943	0,732	0,252	0,974	0,82
77	0,955	0,535	0,184	0,981	0,81
78	0,967	0,374	0,129	0,986	0,79
79	0,977	0,242	0,083	0,991	0,78
80	0,982	0,175	0,060	0,994	0,78

Важным фактором работы Call-центра является, чтобы количество операторов было достаточным для обработки всех вызовов. Занятость оператора 81% может являться оптимальной, потому что сотрудник остается бодрым и продуктивным. Данный уровень занятости достигается при числе операторов равным 77.

Таким образом, было найдено оптимальное с количество операторов, при котором величины параметров (занятость оператора, среднее время ожидания, средняя длина очереди, уровень обслуживания и вероятность соединения с оператором без постановки в очередь) будут устраивать заказчика.