вариант 14.. Решение Оптимальное количество вложенного труда обозначим через X определим прибыль
 Скачать 203 Kb. Скачать 203 Kb.
|
|
Задание 1. Объем выпуска продукции Y зависит от количества вложенного труда х, как функция, представленная в таблице. Цена продукции v, зарплата р. Другие издержки не учитываются. Найти оптимальное количество вложенного труда. Решение: Оптимальное количество вложенного труда обозначим через X* Определим прибыль Воспользуемся соотношением 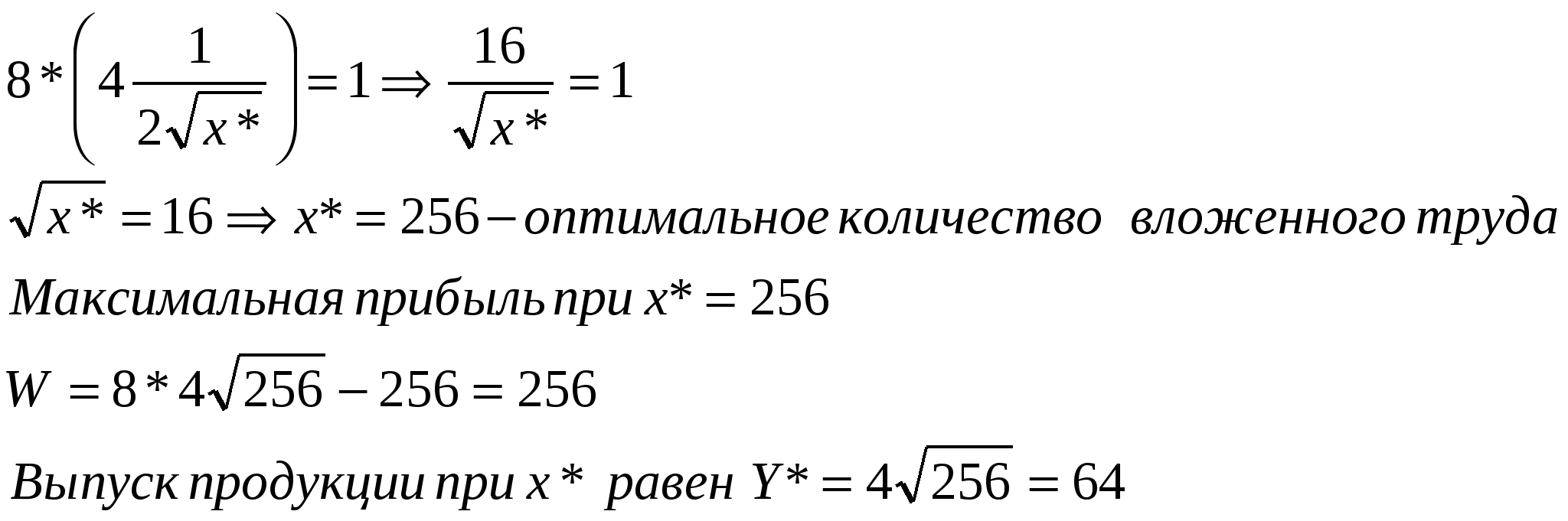 Задание 2. Даны зависимости спроса D и предложения S от цены р. Найдите равновесную цену, при которой выручка максимальна и саму эту максимальную выручку. D = 500 – 10p, S = 200 + 10p Решение: Точка равновесия характеризуется равенством спрос и предложения, т.е. 500 – 10p = 200+10p. Равновесная цена p* = 15 и выручка при равновесной цене W(p*) = p* * D(p*) = p* * S(p*) = 350*15 = 5250. При цене p > p* объем продаж и выручка определяется функцией спроса, при p < p* - предложения. Необходимо найти цену 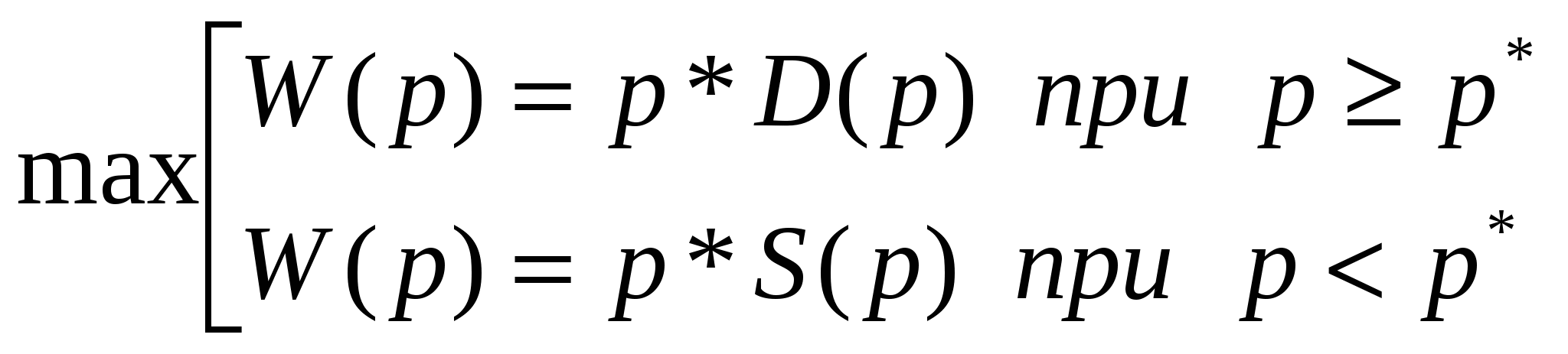 p*(500 – 10p) – функция имеет максимум в точке 25, W(25) = 6250 Таким образом, максимальная выручка W(р) = 6250 достигается не при равновесной цене. Задание 3. Найти решение матричной игры (оптимальные стратегии и цену игры) Решение: 1. Проверяем, имеет ли платежная матрица седловую точку. Если да, то выписываем решение игры в чистых стратегиях. Считаем, что игрок I выбирает свою стратегию так, чтобы получить максимальный свой выигрыш, а игрок II выбирает свою стратегию так, чтобы минимизировать выигрыш игрока I.
Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(ai) = -2, которая указывает на максимальную чистую стратегию A2. Верхняя цена игры b = min(bj) = 2. Что свидетельствует об отсутствии седловой точки, так как a ≠ b, тогда цена игры находится в пределах -2 ≤ y ≤ 2. Находим решение игры в смешанных стратегиях. Объясняется это тем, что игроки не могут объявить противнику свои чистые стратегии: им следует скрывать свои действия. Игру можно решить, если позволить игрокам выбирать свои стратегии случайным образом (смешивать чистые стратегии). 2. Проверяем платежную матрицу на доминирующие строки и доминирующие столбцы. Иногда на основании простого рассмотрения матрицы игры можно сказать, что некоторые чистые стратегии могут войти в оптимальную смешанную стратегию лишь с нулевой вероятностью. Говорят, что i-я стратегия 1-го игрока доминирует его k-ю стратегию, если aij ≥ akj для всех j Э N и хотя бы для одного j aij > akj. В этом случае говорят также, что i-я стратегия (или строка) – доминирующая, k-я – доминируемая. Говорят, что j-я стратегия 2-го игрока доминирует его l-ю стратегию, если для всех j Э M aij ≤ ail и хотя бы для одного i aij < ail. В этом случае j-ю стратегию (столбец) называют доминирующей, l-ю – доминируемой. В платежной матрице отсуствуют доминирующие строки. В платежной матрице отсуствуют доминирующие столбцы. Так как игроки выбирают свои чистые стратегии случайным образом, то выигрыш игрока I будет случайной величиной. В этом случае игрок I должен выбрать свои смешанные стратегии так, чтобы получить максимальный средний выигрыш. Аналогично, игрок II должен выбрать свои смешанные стратегии так, чтобы минимизировать математическое ожидание игрока I. В матрице присутствуют отрицательные элементы. Для упрощения расчетов добавим к элементам матрицы (3). Такая замена не изменит решения игры, изменится только ее цена (по теореме фон Неймана).
3. Находим решение игры в смешанных стратегиях. Математические модели пары двойственных задач линейного программирования можно записать так: найти минимум функции F(x) при ограничениях: 7x1+x2 >= 1 +5x2 >= 1 F(x) = x1+x2 = min найти максимум функции Ф(y) при ограничениях: 7y1 <= 1 y1+5y2 <= 1 Ф(y) = y1+y2 = max Решаем эти системы симплексным методом. Решение симплекс-методом доступно в расширенном режиме. Цена игры будет равна g = 1/F(x), а вероятности применения стратегий игроков: pi = g*xi; qi = g*yi. Цена игры: g = 1 : 11/35 = 32/11 p1 = 32/11 • 4/35 = 4/11 p2 = 32/11 • 1/5 = 7/11 Оптимальная смешанная стратегия игрока I: P = (4/11; 7/11) q1 = 32/11 • 1/7 = 5/11 q2 = 32/11 • 6/35 = 6/11 Оптимальная смешанная стратегия игрока II: Q = (5/11; 6/11) Поскольку ранее к элементам матрицы было прибавлено число (3), то вычтем это число из цены игры. 32/11 - 3 = 2/11 Цена игры: v=2/11 Задание 4. Для трехотраслевой экономической системы заданы матрица коэффициентов прямых материальных затрат 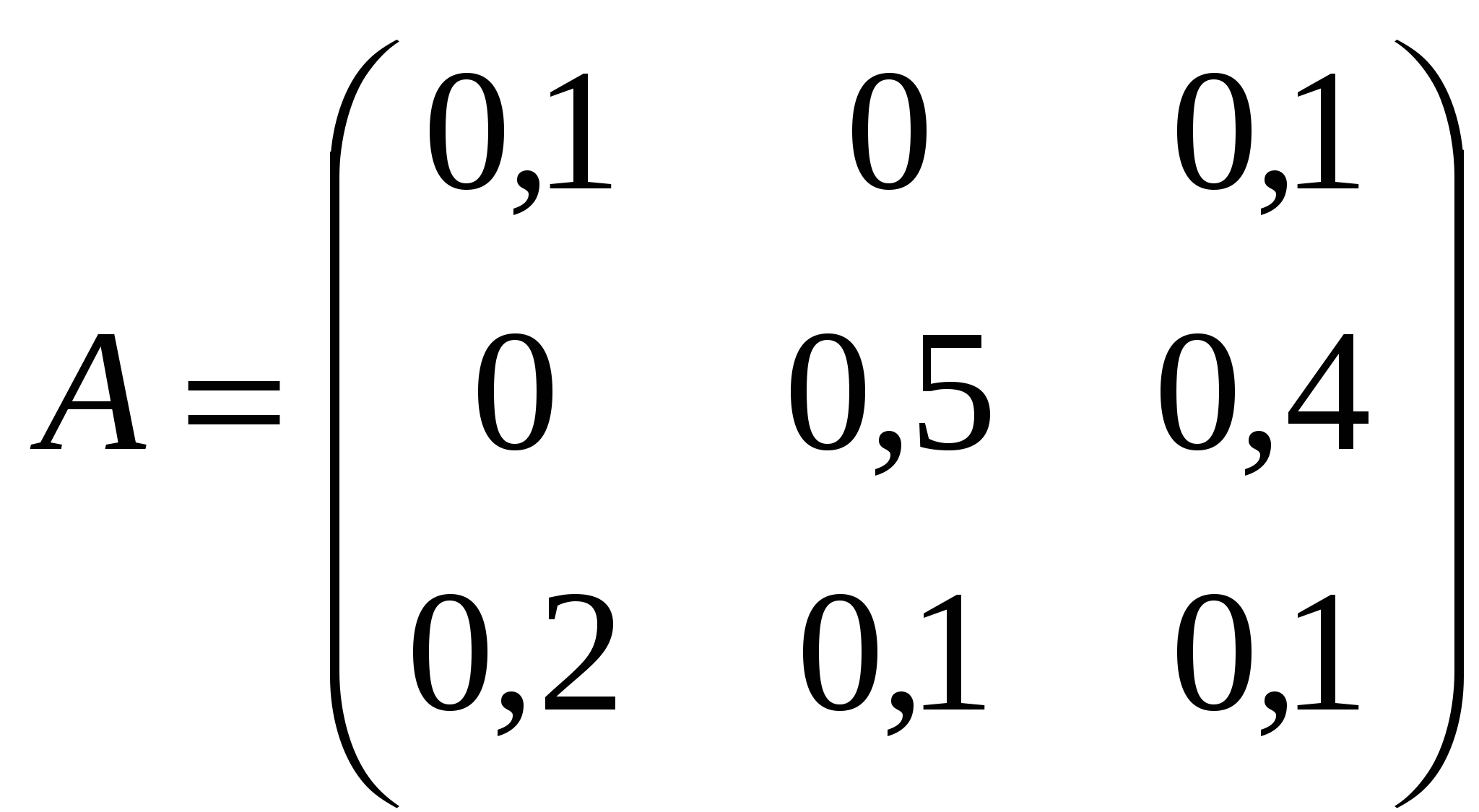 и вектор конечной продукции и вектор конечной продукции 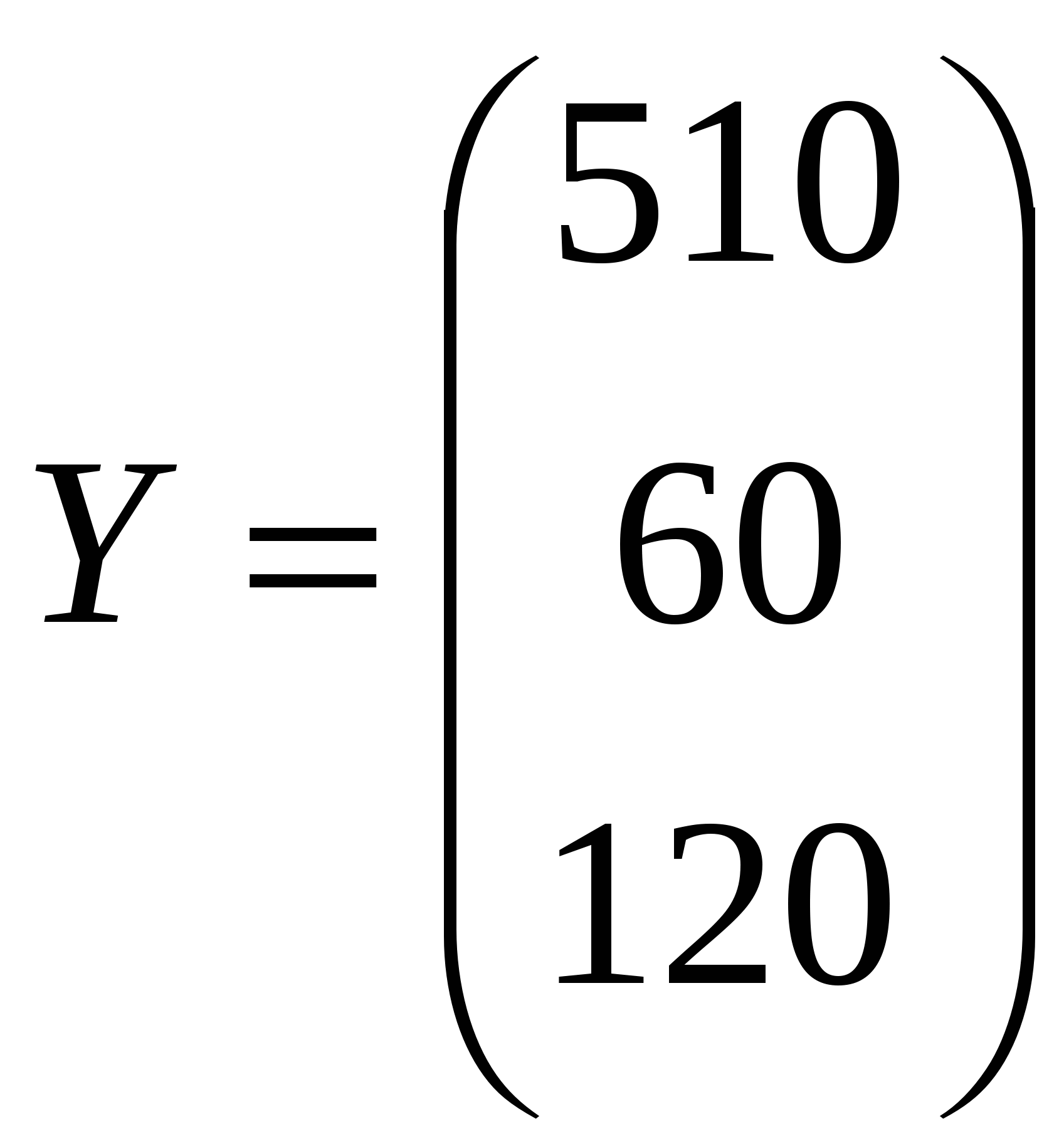 . Найти коэффициенты полных материальных затрат двумя способами (с помощью формул обращения невыраженных матриц и приближённо), заполнить схему межотраслевого баланса. . Найти коэффициенты полных материальных затрат двумя способами (с помощью формул обращения невыраженных матриц и приближённо), заполнить схему межотраслевого баланса.Решение:
Матрица косвенных затрат первого порядка: 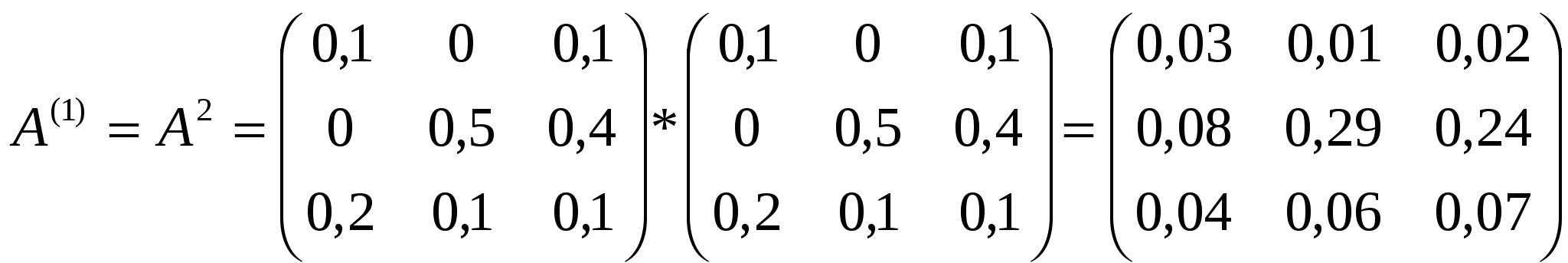 Матрица косвенных затрат второго порядка: 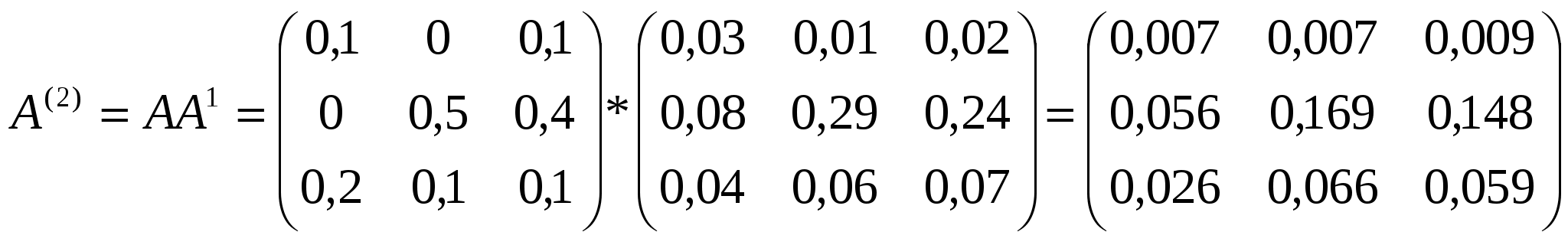 Получаем матрицу коэффициентов полных материальных затрат (приближённо): 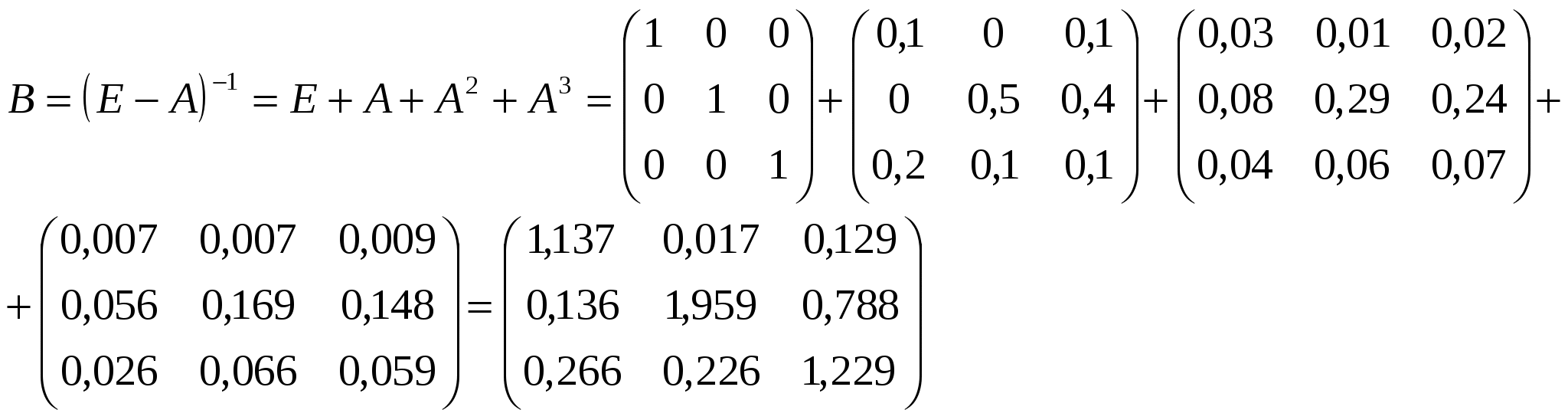
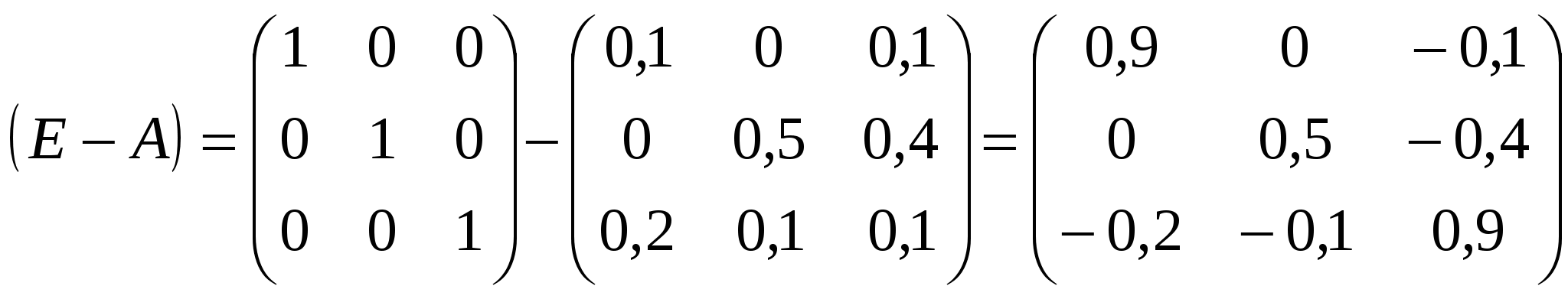
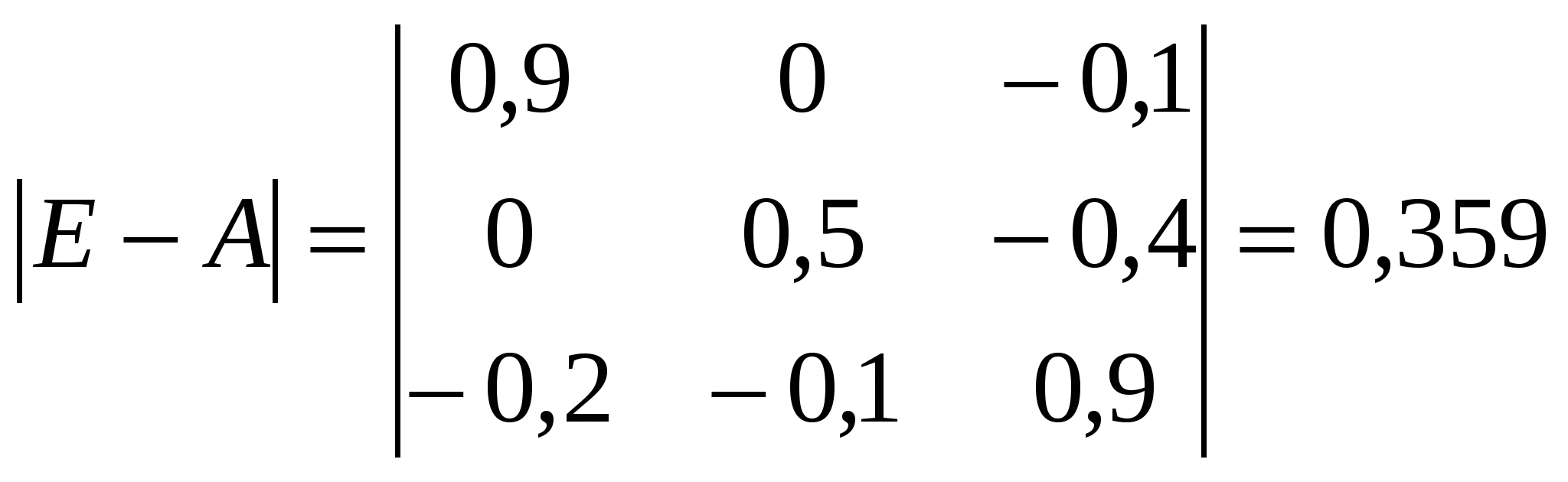
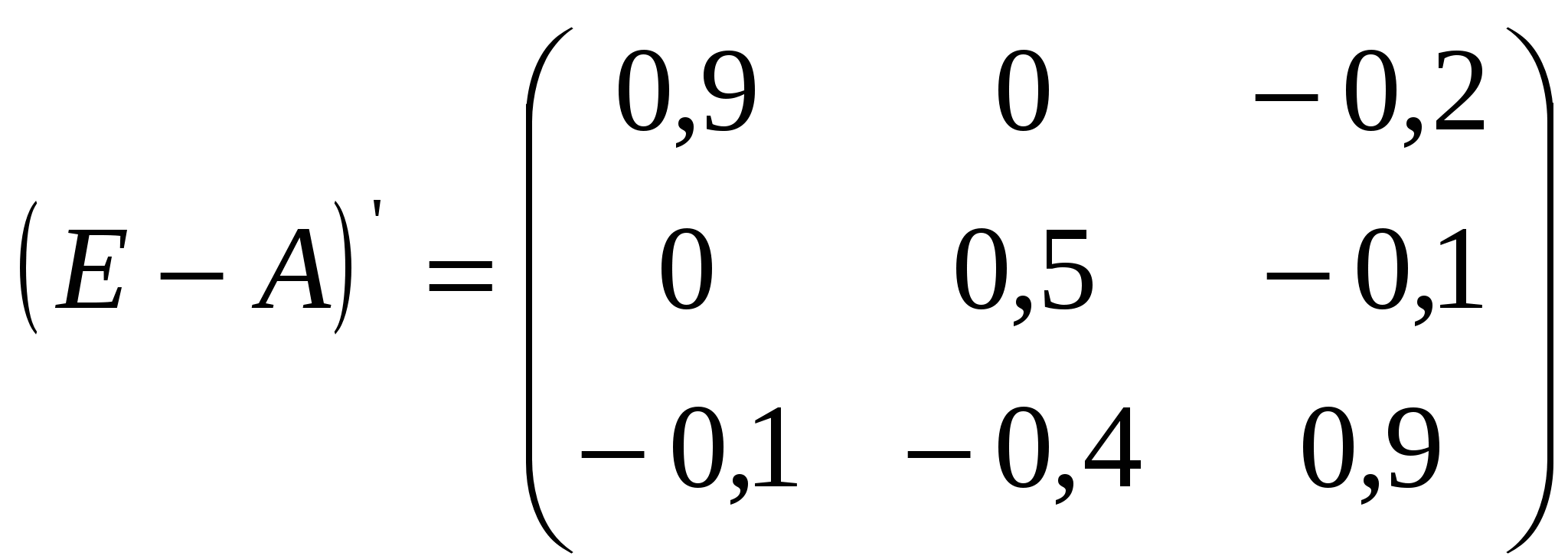
Алгебраические дополнения ∆1,1 = (0.5•0.9-(-0.4•(-0.1))) = 0.41 ∆1,2 = -(0•0.9-(-0.1•(-0.1))) = 0.01 ∆1,3 = (0•(-0.4)-(-0.1•0.5)) = 0.05 ∆2,1 = -(0•0.9-(-0.4•(-0.2))) = 0.08 ∆2,2 = (0.9•0.9-(-0.1•(-0.2))) = 0.79 ∆2,3 = -(0.9•(-0.4)-(-0.1•0)) = 0.36 ∆3,1 = (0•(-0.1)-0.5•(-0.2)) = 0.1 ∆3,2 = -(0.9•(-0.1)-0•(-0.2)) = 0.09 ∆3,3 = (0.9•0.5-0•0) = 0.45 Таким образом: 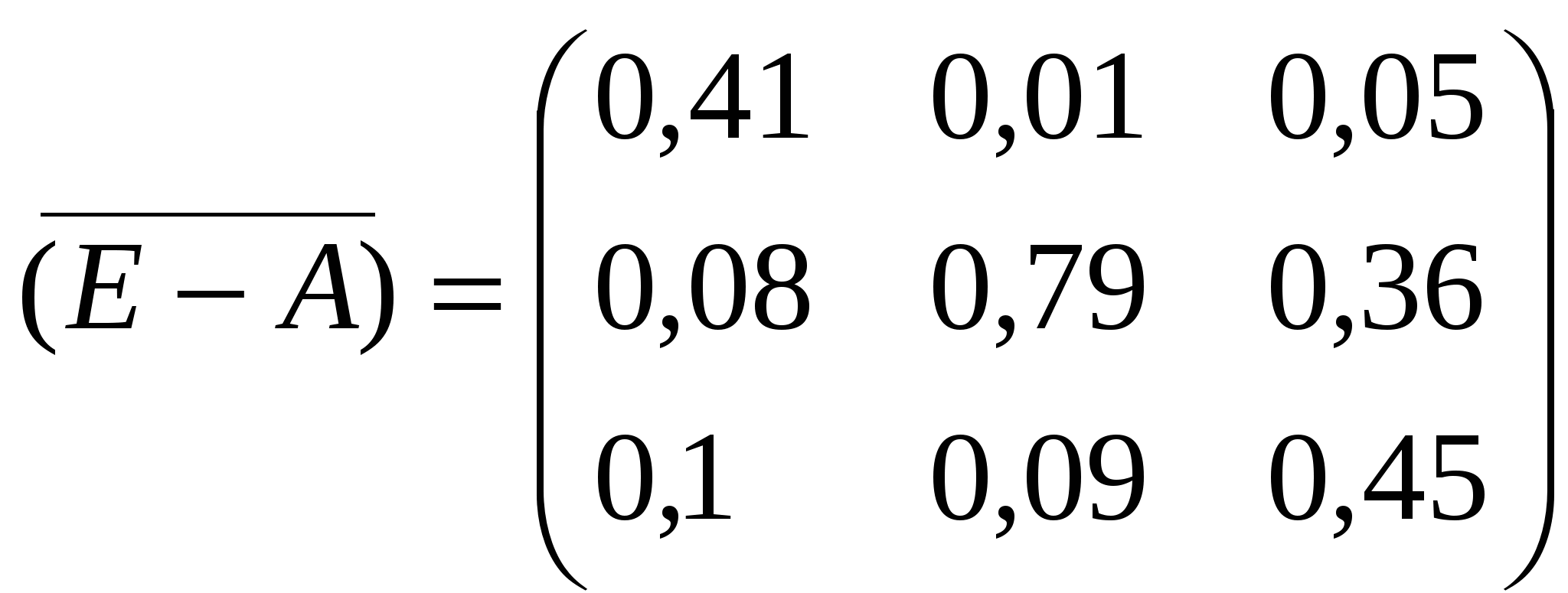
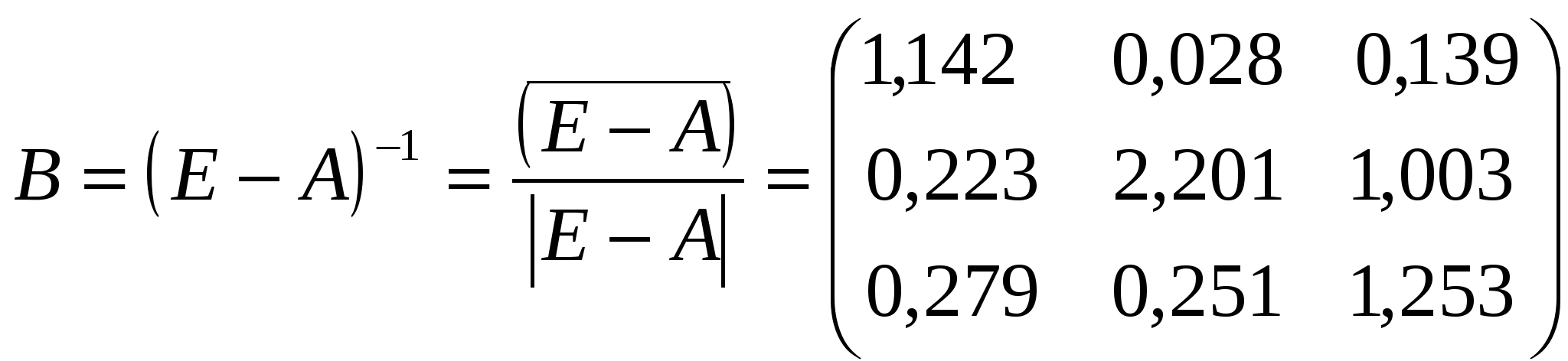 Таким образом, расчёты первым и вторым способом получились разные – это произошло из-за того, что второй способ наиболее точен (рассчитан по точным формулам), а первый способ рассчитан приближённо, без учёта косвенных затрат выше второго порядка. Для заполнения межотраслевого баланса необходимо найти величину валовой продукции: 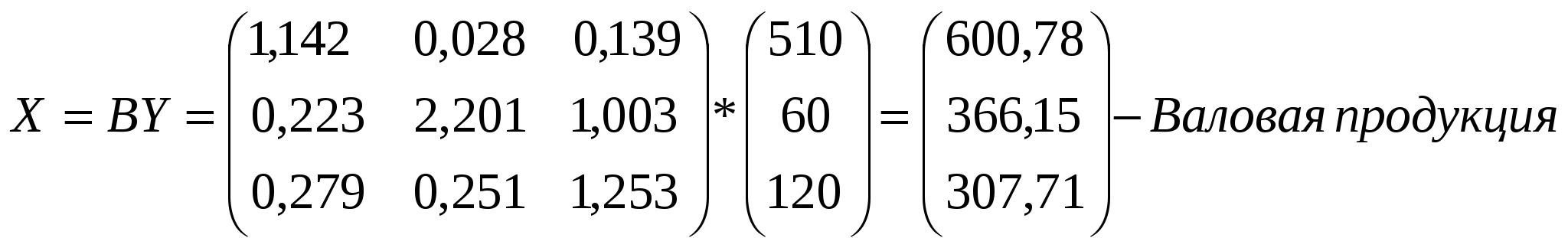 Схема межотраслевого баланса
Задание 5.
Решение:
Для выявления аномальных уровней воспользуемся формулой: 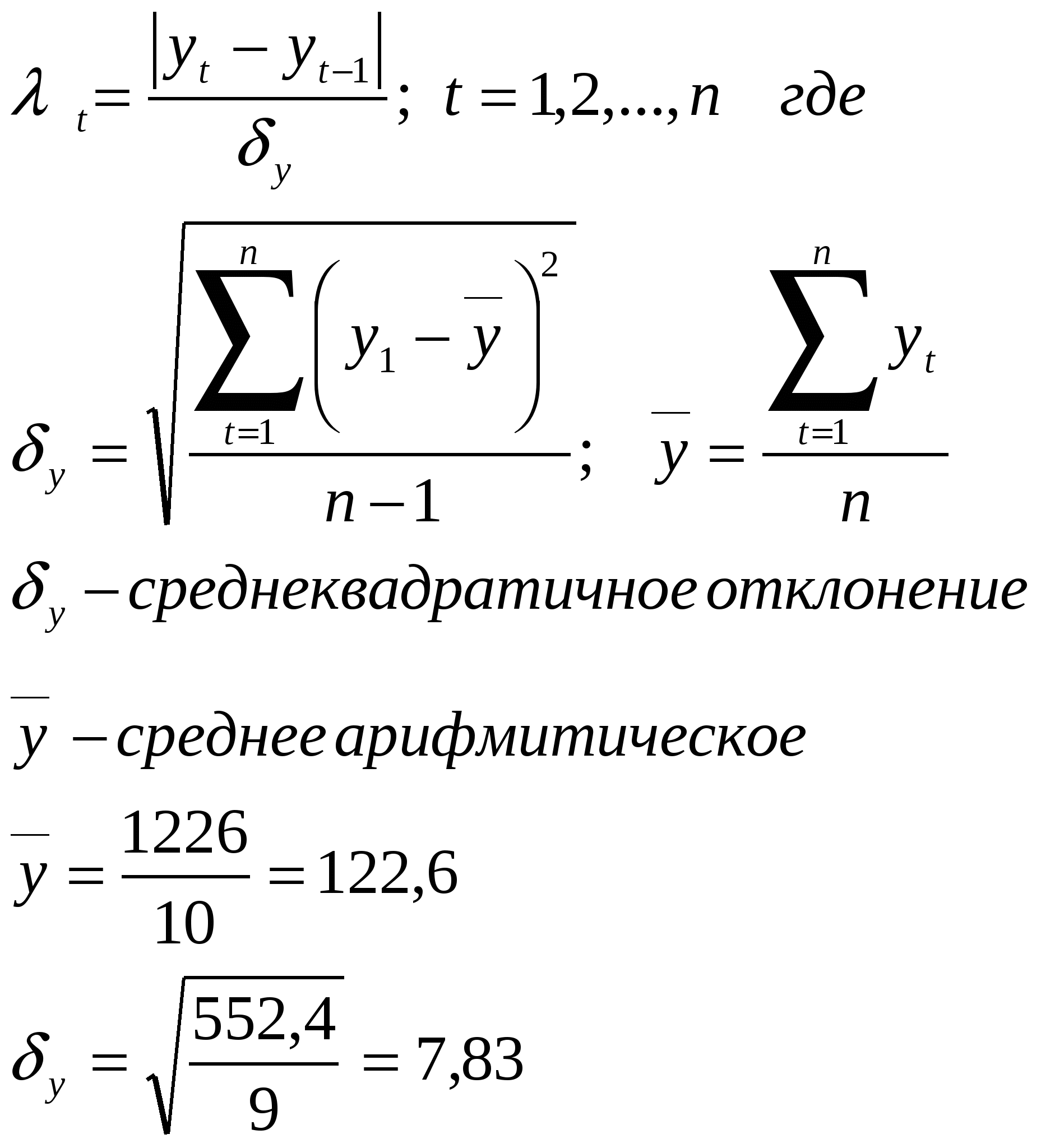 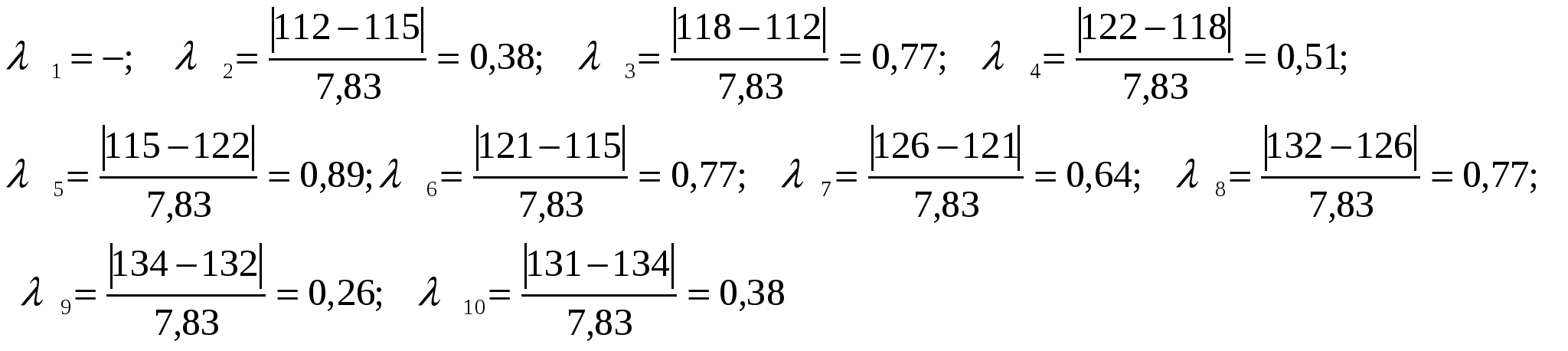 Расчётные значения: Расчётные значения:
Необходимо, расчётные значения сравнить с табличными критерия Ирвина Табличные значения для уровня значимости a=0,05, т.е. с 5% ошибкой:
Таким образом, при сравнении значений, обнаруживаем, что аномальных уровней нет, т.е.
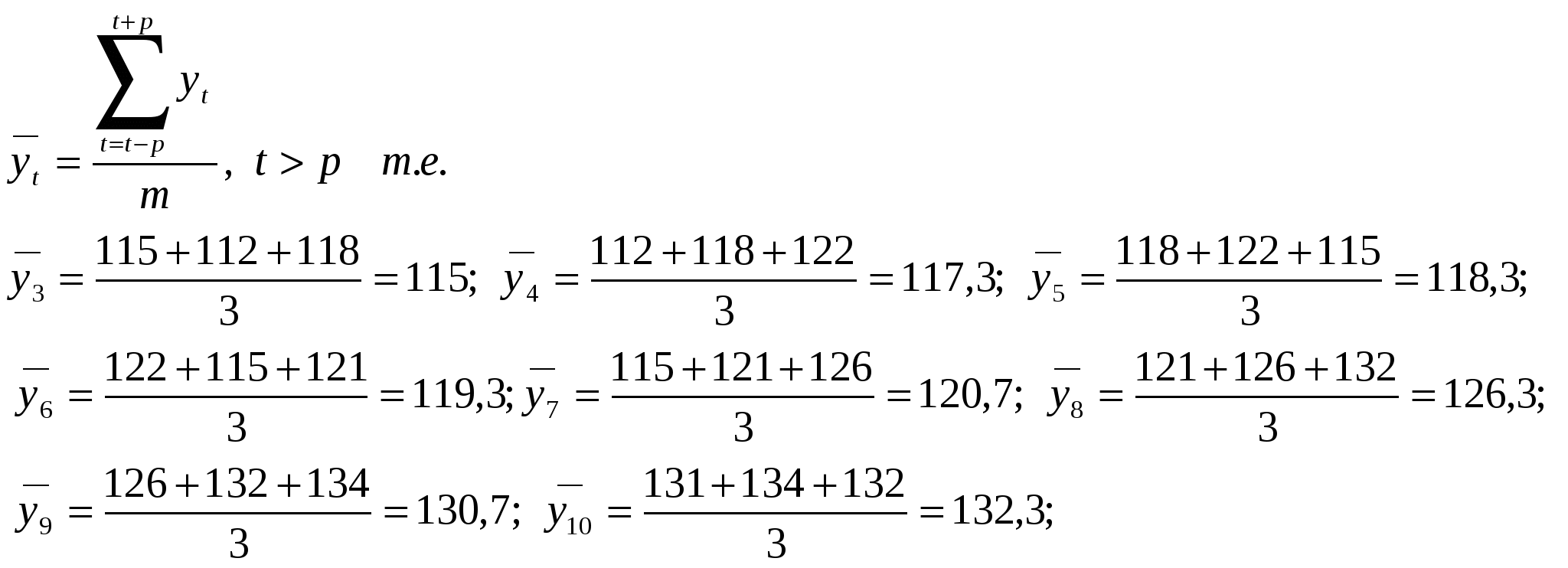

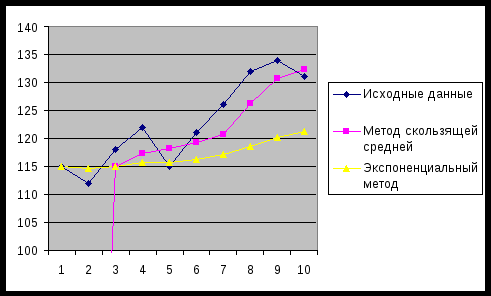
Линейное уравнение тренда имеет вид y = at + b Находим параметры уравнения методом наименьших квадратов. Система уравнений МНК: a0n + a1∑t = ∑y a0∑t + a1∑t2 = ∑y•t
Для наших данных система уравнений имеет вид: 10a0 + 55a1 = 1226 55a0 + 385a1 = 6936 Из первого уравнения выражаем а0 и подставим во второе уравнение Получаем a0 = 2.34, a1 = 109.73 Уравнение тренда y = 2.34 t + 109.73 y(11) = 2.34*11 + 109.73 = 135.47 y(12) = 2.34*12 + 109.73 = 137.81 y(13) = 2.34*13 + 109.73 = 140.15 Задание 6. Пункт по приёму квартир работает в режиме отказа и состоит из двух бригад. Интенсивность потока Решение: Коэффициент использования (количество заявок, поступающих за время использования одной заявки)
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
