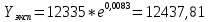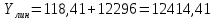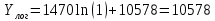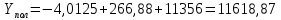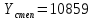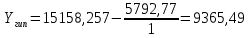3.1 Краткие теоретические сведения
Анализ временного ряда начинается с построения его графика, выявления наличия и характера тренда, наличия и характера сезонности.
Метод аналитического выравнивания позволяет определить проявляющуюся во времени тенденцию развития изучаемого явления. Развитие исследуемого процесса предстает перед исследователем как бы в зависимости только от течения времени. В ходе выравнивания временного ряда получают наиболее общий, суммарный, проявляющийся во времени результат действия всех причинных факторов. Отклонение конкретных уровней ряда от уровней, соответствующих общей тенденции, объясняют действием факторов, проявляющихся случайно или циклически.
Тренд представляет собой общую систематическую линейную или нелинейную компоненту, которая может изменяться во времени, то есть это закономерная, неслучайная составляющая временного ряда, которая может быть вычислена по вполне определенному однозначному правилу. Поэтому обычно предполагают, что тренд - это некоторая функция простого вида (линейная, квадратичная и т.п.), описывающая “поведение в целом” ряда или процесса. В практических исследованиях в качестве модели тренда в основном используют следующие функции: линейную, полиноминальную, степенную, показательную, экспоненциальную. Выбор функции тренда осуществляется по целому ряду статистических критериев, например, по дисперсии, корреляционному отношению, коэффициенту детерминации. При этом критерии являются критериями аппроксимации, а не прогноза.
Таким образом, целью аналитического выравнивания динамического ряда является определение аналитической или графической зависимости. На практике по имеющемуся временному ряду задают вид и находят параметры функции, а затем анализируют отклонение от тенденции. Функцию выбирают таким образом, чтобы она давала содержательное объяснение изучаемого процесса.
Для выявления основной тенденции (тренда) необходимо рассчитать параметры функции, описывающей эмпирический ряд. Наиболее распространенными методами оценки параметров являются:
метод наименьших квадратов и его модификации,
метод экспоненциального сглаживания,
метод вероятностного моделирования и метод адаптивного сглаживания.
Использование методов сглаживания рядов необходимо для того, чтобы исключить возможности «сглаживания» значимых моментов в поведении системы случайных выбросов и кратковременных изменений параметров.
Под сезонными колебаниями понимаются более или менее устойчивые внутригодовые колебания уровней развития социально-экономических явлений.
Большое практическое значение статистического изучения сезонных колебаний состоит в том, что получаемые при анализе рядов внутригодовой динамики количественные характеристики отображают специфику развития изучаемых явлений по месяцам и кварталам годового цикла. Это необходимо для познания закономерностей развития социально-экономических явлений во внутригодовой динамике, прогнозирования и разработки оперативных мер по своевременному управлению их развитием во времени.
При статистическом изучении в рядах внутригодовой динамики сезонных колебаний решаются следующие две взаимосвязанные задачи: выявление специфики развития изучаемого явления во внутригодовой динамике; измерение сезонных колебаний изучаемого явления с построением модели сезонной волны. [2]
Используя установленный программный пакет Microsoft Excel построим график (рисунок 3.1) исходных данных, на котором отобразим 5 видов уравнений тренда (экспоненциальный, линейный, логарифмический, полиномиальный, степенной).
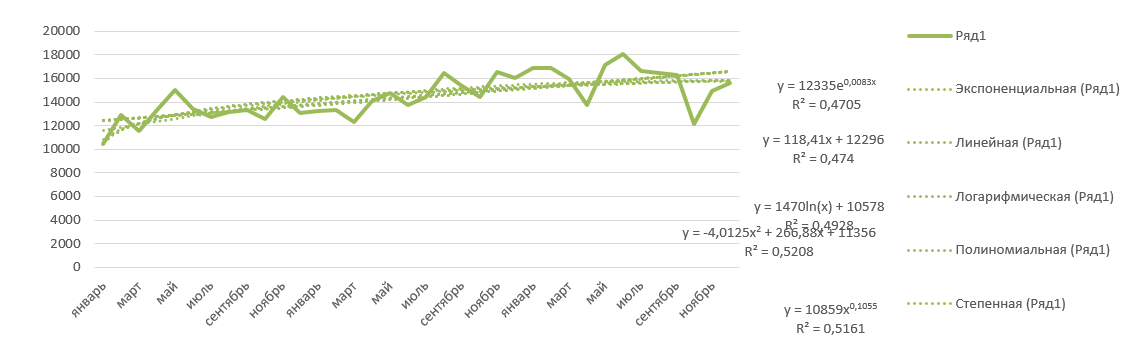
Рисунок 3.1 – График исходных данных и линий тренда
Экспоненциальное уравнение линии тренда имеет вид:
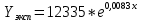 , (3.1) , (3.1)
где х – номер месяца.
Линейное уравнение линии тренда имеет вид:
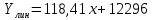 (3.2) (3.2)
Логарифмическое уравнение линии тренда имеет вид:
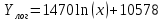 (3.3) (3.3)
Полиномиальное уравнение линии тренда имеет вид:
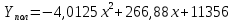 (3.4) (3.4)
Степенное уравнение линии тренда имеет вид:
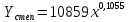 (3.5) (3.5)
Гиперболическое уравнение тренда имеет вид:
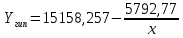 (3.6) (3.6)
Коэффициенты детерминации приведены в таблице 3.1.
Таблица 3.1 – Коэффициенты детерминации для уравнений тренда
Уравнение
|
R2
|
Экспоненциальное
|
0,4705
|
Линейное
|
0,474
|
Логарифмическое
|
0,4928
|
Полиномиальное
|
0,5208
|
Степенное
|
0,5161
|
Гиперболическое
|
0,3769
|
Рассчитаем значения методом аналитического выравнивания:
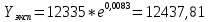
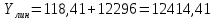
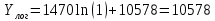
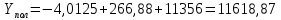
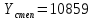
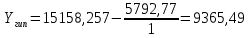
Остальные расчеты сведем в таблицу 3.2.
Таблица 3.2 – Результаты расчета
Номер месяца
|
Исходные данные
|
Экспоненциальная
|
Линейная
|
Логарифмическая
|
Полиномиальная
|
Степенная
|
Гиперболическая
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
1
|
10428
|
12437,807
|
12414,410
|
10578,000
|
11618,868
|
10859,000
|
9365,487
|
2
|
12863
|
12541,470
|
12532,820
|
11596,926
|
11873,710
|
11682,842
|
12261,872
|
3
|
11539
|
12645,997
|
12651,230
|
12192,960
|
12120,528
|
12193,437
|
13227,334
|
4
|
13301
|
12751,396
|
12769,640
|
12615,853
|
12359,320
|
12569,186
|
13710,065
|
5
|
15009
|
12857,673
|
12888,050
|
12943,874
|
12590,088
|
12868,596
|
13999,703
|
6
|
13439
|
12964,836
|
13006,460
|
13211,886
|
12812,830
|
13118,518
|
14192,795
|
7
|
12736
|
13072,892
|
13124,870
|
13438,488
|
13027,548
|
13333,608
|
14330,718
|
8
|
13153
|
13181,848
|
13243,280
|
13634,779
|
13234,240
|
13522,775
|
14434,161
|
9
|
13321
|
13291,713
|
13361,690
|
13807,920
|
13432,908
|
13691,859
|
14514,616
|
10
|
12604
|
13402,493
|
13480,100
|
13962,800
|
13623,550
|
13844,900
|
14578,980
|
11
|
14456
|
13514,197
|
13598,510
|
14102,906
|
13806,168
|
13984,816
|
14631,642
|
12
|
13112
|
13626,831
|
13716,920
|
14230,813
|
13980,760
|
14113,784
|
14675,526
|
13
|
13281
|
13740,405
|
13835,330
|
14348,476
|
14147,328
|
14233,472
|
14712,659
|
14
|
13354
|
13854,925
|
13953,740
|
14457,414
|
14305,870
|
14345,191
|
14744,488
|
15
|
12293
|
13970,399
|
14072,150
|
14558,834
|
14456,388
|
14449,987
|
14772,072
|
16
|
14075
|
14086,836
|
14190,560
|
14653,705
|
14598,880
|
14548,710
|
14796,209
|
17
|
14731
|
14204,243
|
14308,970
|
14742,824
|
14733,348
|
14642,060
|
14817,506
|
18
|
13731
|
14322,629
|
14427,380
|
14826,846
|
14859,790
|
14730,622
|
14836,436
|
19
|
14412
|
14442,002
|
14545,790
|
14906,325
|
14978,208
|
14814,887
|
14853,374
|
20
|
16463
|
14562,369
|
14664,200
|
14981,726
|
15088,600
|
14895,274
|
14868,619
|
21
|
15391
|
14683,740
|
14782,610
|
15053,448
|
15190,968
|
14972,143
|
14882,411
|
22
|
14424
|
14806,122
|
14901,020
|
15121,832
|
15285,310
|
15045,805
|
14894,949
|
23
|
16517
|
14929,524
|
15019,430
|
15187,176
|
15371,628
|
15116,530
|
14906,397
|
24
|
16003
|
15053,955
|
15137,840
|
15249,739
|
15449,920
|
15184,557
|
14916,892
|
Продолжение таблицы 3.2
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
25
|
16887
|
15179,423
|
15256,250
|
15309,747
|
15520,188
|
15250,093
|
14926,546
|
26
|
16884
|
15305,936
|
15374,660
|
15367,402
|
15582,430
|
15313,326
|
14935,458
|
27
|
15935
|
15433,504
|
15493,070
|
15422,880
|
15636,648
|
15374,419
|
14943,710
|
28
|
13786
|
15562,135
|
15611,480
|
15476,341
|
15682,840
|
15433,521
|
14951,372
|
29
|
17147
|
15691,839
|
15729,890
|
15527,925
|
15721,008
|
15490,763
|
14958,506
|
30
|
18111
|
15822,623
|
15848,300
|
15577,760
|
15751,150
|
15546,267
|
14965,165
|
31
|
16663
|
15954,497
|
15966,710
|
15625,961
|
15773,268
|
15600,140
|
14971,393
|
32
|
16442
|
16087,471
|
16085,120
|
15672,632
|
15787,360
|
15652,480
|
14977,233
|
33
|
16325
|
16221,552
|
16203,530
|
15717,866
|
15793,428
|
15703,377
|
14982,719
|
34
|
12145
|
16356,752
|
16321,940
|
15761,750
|
15791,470
|
15752,912
|
14987,881
|
35
|
14933
|
16493,078
|
16440,350
|
15804,362
|
15781,488
|
15801,161
|
14992,749
|
36
|
15621
|
16630,540
|
16558,760
|
15845,773
|
15763,480
|
15848,193
|
14997,347
|
Рассчитаем сезонные компоненты S для каждого вида зависимости.
Для этого найдем разницу между фактическими значения и значениями тренда, затем найдем среднее значение разницы за 3 года для каждого месяца (обозначим Yср). Затем определим общее среднее значение разницы за 3 года (Yср.общ). Тогда сезонная компонента для каждого месяца будет находиться по формуле (3.7).
S = Yср i – Yср.общ (3.7)
Сведем расчеты сезонных компоненты для всех видов зависимости в таблицы 3.3-3.8.
Таблица 3.3 – Расчет сезонной компоненты для экспоненциальной зависимости
Рассчитанные разницы
|
|
|
1-ый год
|
2-ой год
|
3-ий год
|
Среднее значение, Yср
|
Сезонная компонента, S
|
-2009,807
|
-459,405
|
1707,577
|
-253,878
|
-304,693
|
321,530
|
-500,925
|
1578,064
|
466,223
|
415,408
|
-1106,997
|
-1677,399
|
501,496
|
-760,967
|
-811,782
|
549,604
|
-11,836
|
-1776,135
|
-412,789
|
-463,604
|
2151,327
|
526,757
|
1455,161
|
1377,748
|
1326,933
|
474,164
|
-591,629
|
2288,377
|
723,637
|
672,822
|
-336,892
|
-30,002
|
708,503
|
113,870
|
63,055
|
-28,848
|
1900,631
|
354,529
|
742,104
|
691,289
|
29,287
|
707,260
|
103,448
|
279,998
|
229,183
|
-798,493
|
-382,122
|
-4211,752
|
-1797,456
|
-1848,271
|
941,803
|
1587,476
|
-1560,078
|
323,067
|
272,252
|
-514,831
|
949,045
|
-1009,540
|
-191,775
|
-242,591
|
Yср.общ
|
|
|
|
|
50,815
|
|
|
|
|
Таблица 3.4 – Расчет сезонной компоненты для линейной зависимости
Рассчитанные разницы
|
|
|
1-ый год
|
2-ой год
|
3-ий год
|
Среднее значение, Yср
|
Сезонная компонента, S
|
-1986,410
|
-554,330
|
1630,750
|
-303,330
|
-303,273
|
330,180
|
-599,740
|
1509,340
|
413,260
|
413,317
|
-1112,230
|
-1779,150
|
441,930
|
-816,483
|
-816,426
|
531,360
|
-115,560
|
-1825,480
|
-469,893
|
-469,836
|
2120,950
|
422,030
|
1417,110
|
1320,030
|
1320,087
|
432,540
|
-696,380
|
2262,700
|
666,287
|
666,344
|
-388,870
|
-133,790
|
696,290
|
57,877
|
57,934
|
-90,280
|
1798,800
|
356,880
|
688,467
|
688,524
|
-40,690
|
608,390
|
121,470
|
229,723
|
229,781
|
-876,100
|
-477,020
|
-4176,940
|
-1843,353
|
-1843,296
|
857,490
|
1497,570
|
-1507,350
|
282,570
|
282,627
|
-604,920
|
865,160
|
-937,760
|
-225,840
|
-225,783
|
Yср.общ
|
|
|
|
|
-0,057
|
|
|
|
|
Таблица 3.5 – Расчет сезонной компоненты для логарифмической зависимости
Рассчитанные разницы
|
|
|
1-ый год
|
2-ой год
|
3-ий год
|
Среднее значение, Yср
|
Сезонная компонента, S
|
-150,000
|
-1067,476
|
1577,253
|
119,926
|
119,952
|
1266,074
|
-1103,414
|
1516,598
|
559,752
|
559,779
|
-653,960
|
-2265,834
|
512,120
|
-802,558
|
-802,532
|
685,147
|
-578,705
|
-1690,341
|
-527,966
|
-527,940
|
2065,126
|
-11,824
|
1619,075
|
1224,126
|
1224,152
|
227,114
|
-1095,846
|
2533,240
|
554,836
|
554,862
|
-702,488
|
-494,325
|
1037,039
|
-53,258
|
-53,232
|
-481,779
|
1481,274
|
769,368
|
589,621
|
589,647
|
-486,920
|
337,552
|
607,134
|
152,589
|
152,615
|
-1358,800
|
-697,832
|
-3616,750
|
-1891,127
|
-1891,101
|
353,094
|
1329,824
|
-871,362
|
270,519
|
270,545
|
-1118,813
|
753,261
|
-224,773
|
-196,775
|
-196,748
|
Yср.общ
|
|
|
|
|
-0,026
|
|
|
|
|
Таблица 3.6 – Расчет сезонной компоненты для полиномиальной зависимости
Рассчитанные разницы
|
|
|
1-ый год
|
2-ой год
|
3-ий год
|
Среднее значение, Yср
|
Сезонная компонента, S
|
-1190,868
|
-866,327
|
1366,813
|
-230,128
|
-229,669
|
989,290
|
-951,870
|
1301,570
|
446,330
|
446,788
|
-581,528
|
-2163,388
|
298,353
|
-815,521
|
-815,062
|
941,680
|
-523,880
|
-1896,840
|
-493,013
|
-492,555
|
2418,913
|
-2,347
|
1425,993
|
1280,853
|
1281,311
|
626,170
|
-1128,790
|
2359,850
|
619,077
|
619,535
|
-291,548
|
-566,208
|
889,733
|
10,659
|
11,118
|
-81,240
|
1374,400
|
654,640
|
649,267
|
649,725
|
-111,908
|
200,033
|
531,573
|
206,566
|
207,024
|
-1019,550
|
-861,310
|
-3646,470
|
-1842,443
|
-1841,985
|
649,833
|
1145,373
|
-848,487
|
315,573
|
316,031
|
-868,760
|
553,080
|
-142,480
|
-152,720
|
-152,262
|
Yср.общ
|
|
|
|
|
-0,459
|
|
|
|
|
Таблица 3.7 – Расчет сезонной компоненты для степенной зависимости
Рассчитанные разницы
|
|
|
1-ый год
|
2-ой год
|
3-ий год
|
Среднее значение, Yср
|
Сезонная компонента, S
|
-431,000
|
-952,472
|
1636,907
|
84,478
|
29,317
|
1180,158
|
-991,191
|
1570,674
|
586,547
|
531,386
|
-654,437
|
-2156,987
|
560,581
|
-750,281
|
-805,442
|
731,814
|
-473,710
|
-1647,521
|
-463,139
|
-518,300
|
2140,404
|
88,940
|
1656,237
|
1295,193
|
1240,033
|
320,482
|
-999,622
|
2564,733
|
628,531
|
573,370
|
-597,608
|
-402,887
|
1062,860
|
20,789
|
-34,372
|
-369,775
|
1567,726
|
789,520
|
662,490
|
607,330
|
-370,859
|
418,857
|
621,623
|
223,207
|
168,046
|
-1240,900
|
-621,805
|
-3607,912
|
-1823,539
|
-1878,700
|
471,184
|
1400,470
|
-868,161
|
334,497
|
279,337
|
-1001,784
|
818,443
|
-227,193
|
-136,844
|
-192,005
|
Yср.общ
|
|
|
|
|
55,161
|
|
|
|
|
Таблица 3.8 – Расчет сезонной компоненты для гиперболической зависимости
Рассчитанные разницы
|
|
|
1-ый год
|
2-ой год
|
3-ий год
|
Среднее значение, Yср
|
Сезонная компонента, S
|
1062,513
|
-1431,659
|
1960,454
|
530,436
|
530,436
|
601,128
|
-1390,488
|
1948,542
|
386,394
|
386,394
|
-1688,334
|
-2479,072
|
991,290
|
-1058,705
|
-1058,706
|
-409,065
|
-721,209
|
-1165,372
|
-765,215
|
-765,216
|
1009,297
|
-86,506
|
2188,494
|
1037,095
|
1037,095
|
-753,795
|
-1105,436
|
3145,835
|
428,868
|
428,868
|
-1594,718
|
-441,374
|
1691,607
|
-114,829
|
-114,829
|
-1281,161
|
1594,382
|
1464,767
|
592,663
|
592,662
|
-1193,616
|
508,589
|
1342,281
|
219,085
|
219,085
|
-1974,980
|
-470,949
|
-2842,881
|
-1762,937
|
-1762,937
|
-175,642
|
1610,603
|
-59,749
|
458,404
|
458,404
|
-1563,526
|
1086,108
|
623,653
|
48,745
|
48,745
|
Yср.общ
|
|
|
|
|
0,0002
|
|
|
|
|
Рассчитаем точность построенных моделей. Для этого найдем значение ошибки по формуле (3.8) и среднеквадратическое отклонение по формуле (3.9).
|
 Скачать 290.47 Kb.
Скачать 290.47 Kb.
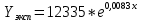 , (3.1)
, (3.1)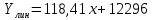 (3.2)
(3.2)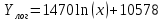 (3.3)
(3.3)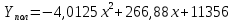 (3.4)
(3.4)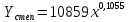 (3.5)
(3.5)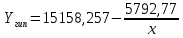 (3.6)
(3.6)