2. Курсовая работа РКМЧП младших школьников. Курсовая работа по теме Методы развития критического мышления как средство когнитивного развития младших школьников Работу
 Скачать 310.15 Kb. Скачать 310.15 Kb.
|
|
ГЛАВА 2. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ТЕХНОЛОГИИ КРИТИЧЕСКОГО МЫШЛЕНИЯ КАК СРЕДСТВА КОГНИТИВНОГО РАЗВИТИЯ МЛАДШИХ ШКОЛЬНИКОВ 2.1. Педагогические условия для развития критического мышления младших школьников Для эффективного процесса развития критического мышления младших школьников, необходимо соблюдать педагогические условия: Учет индивидуальных особенностей младших школьников для развития критического мышления; Анализ практического опыта применения методических приёмов РКМЧП в различных областях учебных предметов; Диагностика уровня сформированности критического мышления младших школьников. Рассмотрим подробно каждое из перечисленных условий. Учет индивидуальных особенностей для развития критического мышления Каждый возрастной этап развития личности характеризуется образованием общих и индивидуальных особенностей. Дети одного и того же возраста отличаются друг от друга мышлением, физическим и духовным развитием, способностями к обучению, личными интересами. Учитель уже с первого класса, изучив психологические возможности своих учеников, строит учебный процесс, применяя личностно-дифференцированный подход. Дифференцированный подход предполагает разумное сочетание фронтальных, групповых и индивидуальных форм работы. Суть такого подхода заключается в условном разделении класса на несколько подвижных групп, на определенных этапах урока в зависимости от учебных возможностей учащихся. Каждая группа овладевает навыками и умениями в различном темпе, имеет свой вариант. Осуществляя дифференцированный подход в обучении, можно использовать разнообразные формы индивидуального обучения: - разные варианты однотипных заданий; - задания разных степеней сложности; - помощь учащимся при выполнении задания; - временной режим для выполнения задания; - разные виды ключей, опор, схем, алгоритмов и т.д. Как видно, индивидуальный подход предполагает разные по трудности и сложности задания для достижения одних и тех же конечных целей обучения. Индивидуальный обучение строится в основном на подборе индивидуальных заданий, в зависимости от подготовки учеников, их психологических, личностных особенностей, с учетом затруднений учащихся. Индивидуальные задания, в свою очередь, неэффективны и невозможны без учета психологической структуры личности. [31] При работе с дифференцированными заданиями важно учитывать зону актуального и ближайшего развития. А для этого важно осуществлять постоянный контроль за результатами работы, диагностику и анализ результатов после изучения каждой темы, и в ходе изучения темы. Виды дифференцированных заданий зависят от цели, которую ставит учитель. По уровню трудностей: облегченный, средний, повышенный; Общее для всего класса задание с предложениями системы дополнительных упражнений возрастающей степени трудностей; Индивидуальные дифференцированные задания (карточки, дидактический материал); Групповые дифференцированные задания с учетом различной подготовленности учащихся; Равноценные вариативные задания с приложением к каждому варианту системы дополнительных заданий возрастающей трудности; Упражнения с указанием минимального и максимально количества заданий для обязательного выполнения. Если успех обучения каждого учащегося и развитие критического мышления волнует учителя, то он обязательно будет осуществлять индивидуальный подход в обучении. [1] Анализ практического опыта применения методических приёмов РКМЧП в различных областях учебных предметов Рассмотрим применение некоторых методических приёмов РМЧП на уроках математики в начальной школе. Применение методического приёма «Идеал» Пример использования стратегии «Идеал» при работе с текстовой задачей (3 класс). Задача. В третьем классе учатся 25 учеников. Им было предложено заниматься в 2 кружках: по математике и по природоведению. В каждый кружок записалось по 16 человек, причем 10 человек решили заниматься одновременно математикой и природоведением. Получив результаты, ребята удивились: «Можно подумать, что у нас в классе не 25 учеников, а все 42». Но один любитель математики сказал: «Вовсе нет! У нас есть несколько ребят, которые не хотят заниматься ни в одном из кружков. Я даже могу сказать, сколько их». Как он это узнал? 1 этап. «Интересно, в чем проблема?» - Сформулируйте проблему, начиная со слова «Как…?» Примерные варианты ответов: Как решить задачу? Как узнать, сколько ребят не хотят заниматься ни в одном кружке? Как любитель математики узнал, сколько ребят не занималось ни в одном кружке? Как узнать, сколько ребят не хотят заниматься ни в одном кружке, зная, что из 25 человек в каждый кружок записалось по 16 человек, причем 10 человек решили заниматься в двух кружках одновременно? И т.д. Останавливаемся на одной из формулировок и переходим к следующему этапу. 2 этап. - Предложите как можно больше вариантов решения. На раздумие даётся 10 минут. - Сначала необходимо узнать, сколько ребят собирается заниматься только природоведением и только математикой. Сколько ребят, которые не хотят заниматься ни в одном из кружков. И т.д. - Кто может предложить хорошие решения? 3 этап первичной оценки. - Отметим «+» те способы, которые могут быть осуществимы. Сделайте выбор! - Из тех вариантов, что отмечены «+», выберем самый удачный. - Теперь составим план действий. 1. Найти количество учеников, которые будут заниматься только математикой. 2. Найти количество учеников, которые будут заниматься только природоведением. 3. Найти количество человек, записавшихся в кружки. 4. Найти количество человек, которые не записались в кружки. - Сейчас математическим языком запишем наш план. 1) 16 – 10 = 6 (чел.) – будут заниматься только математикой; 2) 16 – 10 = 6 (чел.) – будут заниматься только природоведением; 3) 6 + 6 + 10 = 22 (чел.) – записались в кружки; 4) 25 – 22 = 3 (чел.) Ответ: 3 учащихся класса не записались ни в один из кружков. Рассмотрим пример применения данного приёма при решении задания (2 класс). На доске записаны числа в таком порядке: 5, 10, 15, 20, … - Внимательно рассмотрите числа. Подумайте, в чём заключается закономерность, на основании которой записаны эти три числа. Назовите следующие три числа. 1 этап. «Интересно, в чем проблема?» - Сформулируйте проблему, начиная со слова «Как…?» Примерные варианты: Как найти закономерность? Как найти следующие три числа? Как найти закономерность, для того, чтобы найти следующие три числа? 2 этап. - Предложите как можно больше вариантов решения. На предложение вариантов решения даётся 10 минут. Примерные варианты: Нужно найти разность соседних чисел; Нужно к последнему числу прибавить разность соседних чисел; Нужно первое число вычесть из второго, второе из третьего, третье из четвертого, чтобы выявить закономерность; Если во всех случаях ответ одинаковый, прибавить его к последнему числу. - Кто может предложить хорошие решения? 3 этап первичной оценки. - Отметим «+» те способы, которые могут быть осуществимы. Сделайте выбор! - Из тех вариантов, что отмечены «+», выберем самый удачный. - Теперь составим план действий. Любопытно, как это будет на практике? - Давайте составим план действий: 1. Из 10 вычесть 5. 2. Из 15 вычесть 10. 3. Из 20 вычесть 15. 4. Сравнить полученные результаты, сделать вывод. 5. Если полученный результат одинаковый, прибавить его к 20. 6. Еще раз прибавить данный результат к полученному в сложении числу. 7. К последнему числу еще раз прибавить полученный результат. - Сейчас математическим языком запишем наш план. 10 – 5 = 5 15 – 10 = 5 20 – 15 = 5 - Разность всех пар чисел одинакова, значит закономерность заключается в том, что каждое следующее число больше предыдущего на 5. 20 + 5 = 25 25 + 5 = 30 30 + 5 = 35 Применение методического приёма «Фишбон» На доске учитель записывает следующие выражения: 2 + 5 * 3 = 21 2 + 5 * 3 = 17 Запись вызывает удивление детей. Возникает проблемный вопрос: «Как записать этот пример, чтобы получить правильный ответ?». Запишем его в нижнем прямоугольнике. Обсуждая, учащиеся находят всевозможные варианты записи примера. Эти варианты записываются по левую сторону схемы. Затем, для каждого варианта подбирается аргумент, доказывающий его правильность. Аргументы записываются по правую сторону. Последним этапом данной стратегии является запись вывода, который получают учащиеся при анализе всего, о чем говорилось ранее. Вывод записывается в треугольнике (Приложение 1). Применение методического приёма «Мозаика проблем» Пример использования данного приёма при работе по вычислению площади прямоугольника. 1 этап - Мы продолжаем тему «Площадь прямоугольника». Сегодня на уроке вспомним известные способы нахождения площади прямоугольника и узнаем новый. А в конце выберем самый удобный (рациональный) способ нахождения площади прямоугольника. Для того чтобы решить все эти задачи, используем стратегию «Мозаика проблем» (Приложение 2). Разбейтесь на три команды. 2 этап - Давайте вспомним известные способы нахождения площади прямоугольника. Вы будете их называть, а я записывать на листе ватмана (дети называют два способа: измерение с помощью палетки, пересчитывание квадратных единиц). - Я тоже расскажу способ нахождения площади прямоугольника. Необходимо измерить ширину и длину, затем длину умножить на ширину. 3 этап - У нас получилось три способа. Они записаны на ватмане, в разных отсеках. Я вырежу эти отсеки ножницами и раздам каждой команде по одному варианту нахождения площади прямоугольника. 4 этап - Сейчас вы работаете в группах. У каждой команды свой прямоугольник. Вы находите его площадь тем способом, который написан у вас на полученной карточке, проводите необходимые измерения, вычисления и сопровождаете все это записями в тетради. После того, как вы найдете площадь данным способом, вы отдаете карточку соседней команде и получаете новую. Так до тех пор, пока каждая команда не использует все три способа. 5 этап - Сравним результаты, полученные в ходе наших исследований. Что можно сказать о полученных вами результатах? - Результаты одинаковые. 6 этап - Мы вспомнили известные способы нахождения площади прямоугольника и познакомились с новым. Что еще мы должны сделать? - выбрать наиболее удобный способ нахождения площади прямоугольника. - Правильно! Давайте обсудим, какой способ более удобный? Все команды участвуют в обсуждении. Итогом становится вывод о том, что способ нахождения площади прямоугольника с помощью вычисления (умножения длины на ширину) более рациональный, так как не требует особых приспособлений и проводится с меньшей затратой времени, в отличие от других двух способов. В следующем примере рассмотрим применение методического приёма «Мозаика проблем» в работе над задачей (Приложение 3). 1 этап Сегодня на уроке мы будим работать над задачей. Работа будет необычной. Мы сами будим составлять условие, схемы и вопросы на основе данного решения. Все это мы будим делать с использованием стратегии «Мозаика проблем». Разбейтесь на три команды. 2 этап То, что вы будите делать в командах, зафиксировано на ватмане, в разных отсеках. Вы будите последовательно выполнять задания из первого отсека, затем из второго и третьего. После мы сравним, что у вас получилось. 3 этап Послушайте задание. Дано решение задачи: 180 + 180 : 2 4 этап Приступаем к работе в группах. Как только вы выполните задание на первой карточке, поднимаете руку, и я даю вам следующую. Так до тех пор, пока каждая команда не выполнит все три задания. 5 этап Сравним результаты. У кого какие получились задачи, у кого какие схемы, какие вопросы? Делаем вывод, что условия и схемы должны быть одинаковые, а вопросы у всех могли получиться разные. Проверяем соответствие условий, схем и вопросов данному решению. Диагностика уровня сформированности критического мышления младших школьников Исходя из понимания термина "критическое мышление", который обозначает один из видов интеллектуальной деятельности человека, который характеризуется высоким уровнем восприятия, понимания, объективности подхода к окружающему его информационному полю, нами были выделены следующие критерии для выявления уровней развития критического мышления (таблица 2, 3). Критерии_и_показатели_развития_критического_мышления'>Критерии и показатели развития критического мышления Таблица 2
Уровни развития критического мышления Таблица 3
Другими словами, критерии оценки результата в условиях ТКМЧП раскрываются следующими показателями: Оценка (Где ошибка?); Диагноз (В чём причина?); Самоконтроль (Каковы недостатки?); Критика (Согласны ли вы? Опровергните. Приведите контраргументы); Прогноз (Постройте прогноз) 2.2. Опытно-экспериментальная работа по развитию критического мышления младших школьников на уроках математики С целью практического обоснования выводов полученных в ходе теоретического изучения по вопросу развития критического мышления младших школьников было проведено педагогическое исследование. В эксперименте приняли участие 15 учащихся 4-го класса МБОУ СОШ с. Победино. Цель эксперимента: выявление уровня развития критического мышления. Задачи: 1) Разработать тестовый материал для определения уровня развития критического мышления младших школьников. 2) Провести исследовательскую работу и на основе полученных данных выявить уровень развития мыслительных операций учащихся на начало эксперимента. 3) Разработать систему заданий и провести формирующий эксперимент. 4) Разработать тестовый материал для контрольного эксперимента, на основе которого сделать выводы об эффективности разработанной методики. Опытно-экспериментальная работа проводилась в 3 этапа: 1) Констатирующий этап. Был разработан материал и проведен тест, направленный на изучение начального уровня развития критического мышления младших школьников. 2) Формирующий этап заключается во внедрении в учебно-воспитательный процесс системы упражнений, способствующих развитию критического мышления. Была проведена проверочная работа в форме теста, с целью выявления эффективности разработанной системы упражнений. 3) Контролирующий этап. Анализ проведенной работы на 1 и 2 этапах. Констатирующий этап. Для исследования уровня развития критического мышления ученикам была предложена тестовая работа по математике. На данном этапе были разработаны уровни сформированности критического мышления младшего школьника: - Высокий уровень ─ если учащийся набрал более 25 баллов; - Средний уровень ─ если учащийся набирает от 12 до 25 баллов; - Низкий уровень – если учащийся набирает меньше 12 баллов. Предложенная учащимся диагностическая тестовая работа даст нам представление об уровне критического мышления развития у учащихся на начало эксперимента. Результаты тестирования представлены в диаграмме 1. Диаграмма 1. 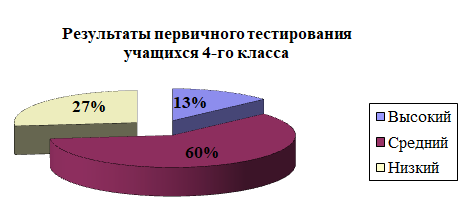 Из данной диаграммы видно, что большой процент класса имеет средний (60%) и низкий уровень (27%) развития мышления. 3 учащихся показали высокий уровень мышления. |
