жбк курсовая. Курсовая работа Расчёт сборных железобетонных конструкций многоэтажного производственного здания Студент гр. 181 Сильченко М. К
 Скачать 5.32 Mb. Скачать 5.32 Mb.
|
1.2 Расчет плиты по прочности(первая группа предельных состояний) Расчет полки плиты. Толщина полки принята h′ƒ = 50 мм. Пролёты полки в свету по рисунку 2: l2 = В1 – 240 мм = 1510 – 240 = 1270 мм. Меньший размер:  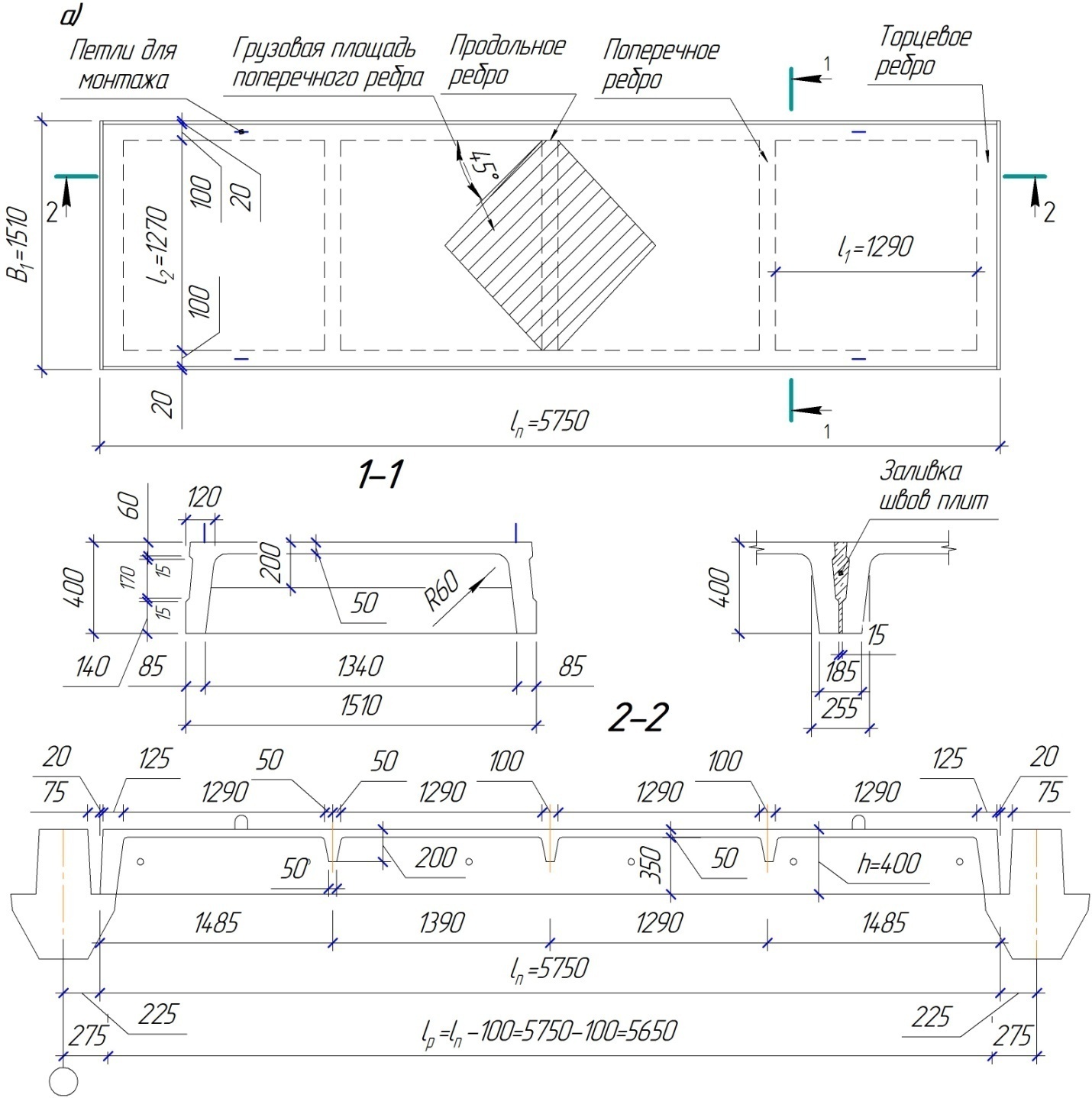 Рисунок 2 – К расчёту ребристой плиты Расчётная нагрузка на 1 м2 полки: Постоянная с коэффициентом надежности по нагрузке γƒ = 1,1: вес полки: γƒ ∙ h′ƒ ∙ ρ = 1,1 ∙ 0,05 ∙ 25 = 1,375 кН/м2, где ρ=25 кН/м3- вес 1 м3 тяжелого железобетона; вес пола и перегородок 1,1 ∙ 2,5 = 2,75 кН/м2. (при отсутствии сведений о конструкции пола и перегородок, их нормативный вес принят 2,5 кН/м2). Итого постоянная нагрузка: g0 = 1,375+2,75 = 4,13 кН/м2. Временная нагрузка (с γƒ = 1,2): p0 = 1,2 ∙ 20 = 24,0 кН/м2. Полная расчётная нагрузка (с γn = 1,0): q= γn (g0+p0)=1,0 (4,13+24) = 28,13 кН/м2. Схема армирования плиты и эпюра моментов в полке плиты представлена на рисунке 3. 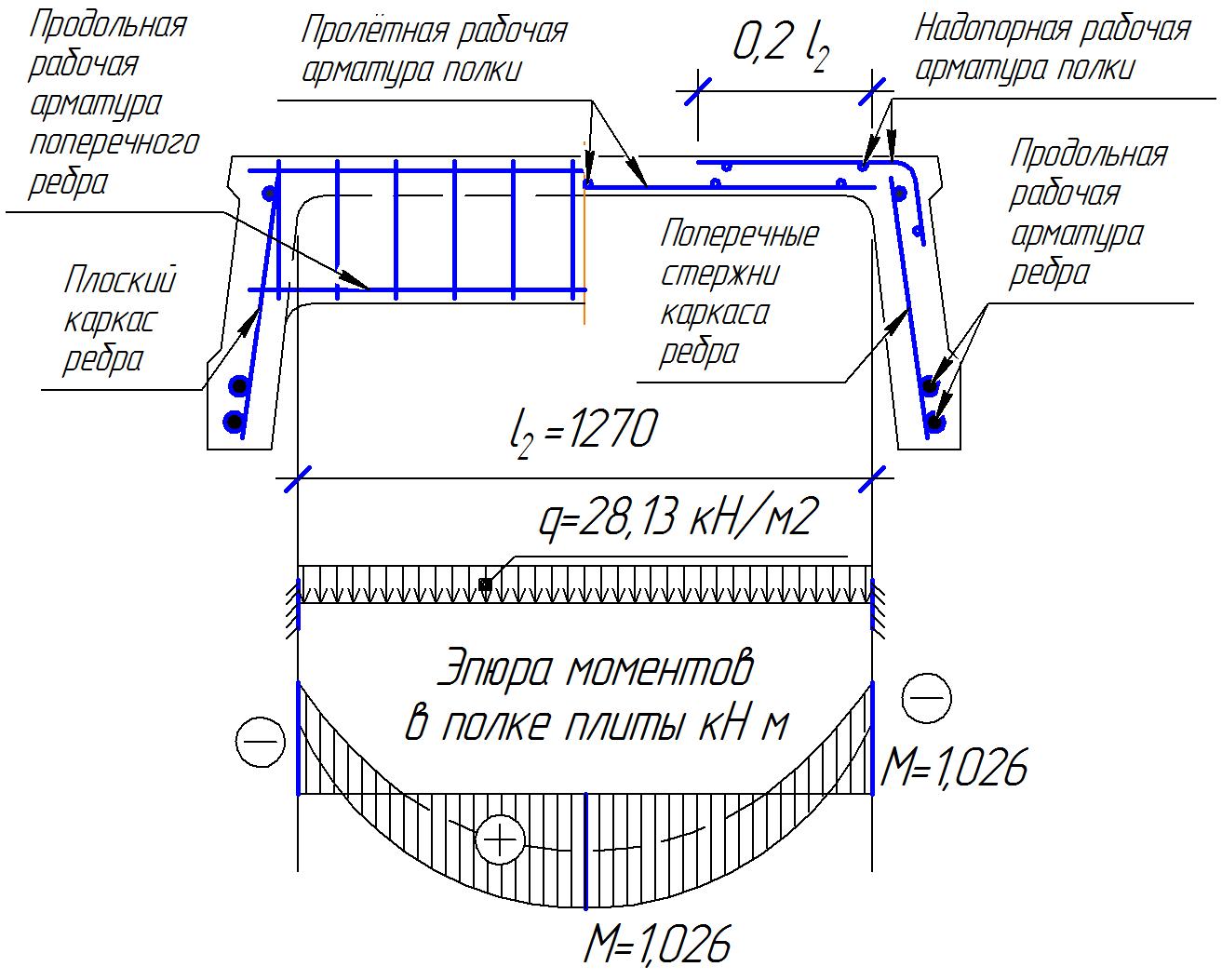 Рисунок 3 – Схема армирования плиты и эпюра М в полке плиты Изгибающий момент в полке (в пролете и на опорах) при прямоугольных полях (l1 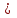 l2): l2):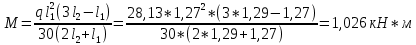 Площадь арматуры при h0 = h – a = 50 – 19 = 31мм (a = защитный слой 15мм + расстояние до середины толщины сетки при арматуре Ø4 В500). Расчетное сопротивление арматуры Rs = 435 МПа (таблица Приложения «В»). 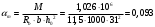 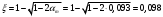 Проверка условия αm < αR:  αR = 0,376 Таким образом, условие αm = 0,093 < αR = 0,376 выполняется 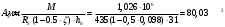 Принята сетка: 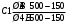 ; Аs =83,8 мм2 (+4,5%) ; Аs =83,8 мм2 (+4,5%)Процент армирования полки: 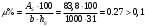 Расчёт поперечных рёбер. Расчёт прочности нормальных сечений Высота ребра hр = 200мм, арматура А400, расчётный пролёт lр =l2= 1270мм. Расчётная нагрузка от собственного веса ребра: 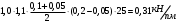 Временная расчётная нагрузка на ширине ребра 0,1м 1,0·24,0·0,10 = 2,4  Расчётная схема ребра, эпюра нагрузки и моментов представлена на рисунке 4. 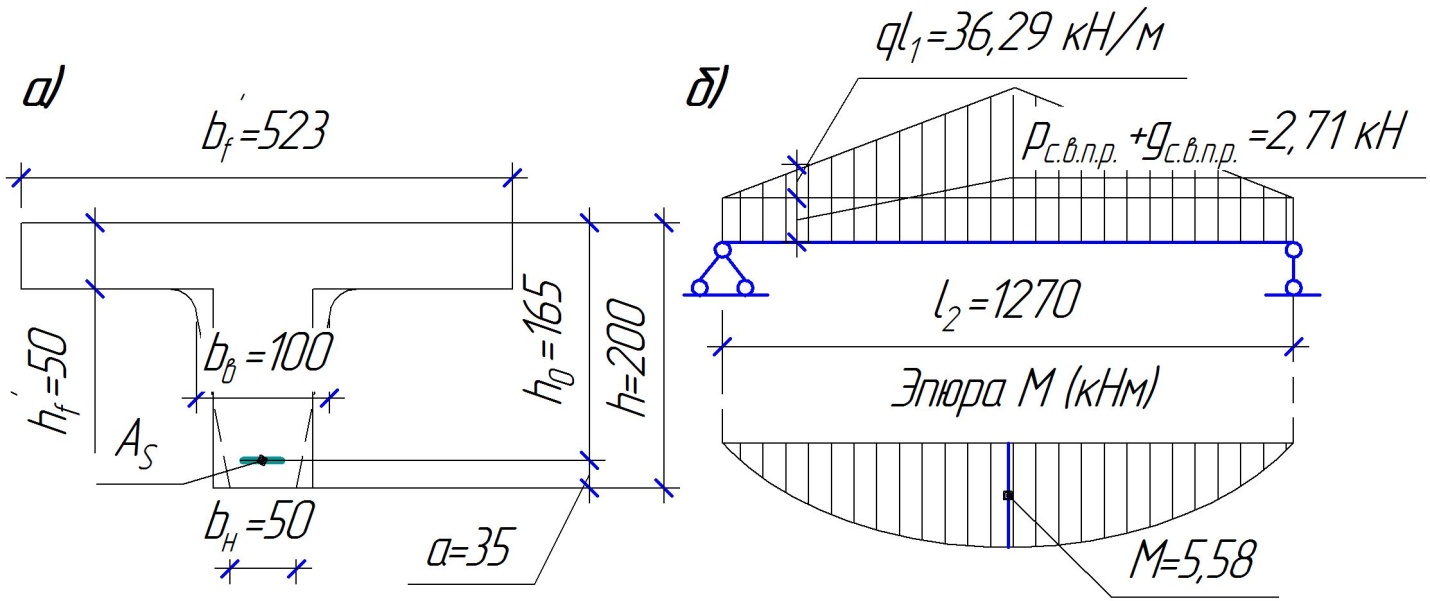 Рисунок 4 – Расчётная схема и эпюра М поперечного ребра Таким образом, изгибающий момент в пролёте поперечного ребра будет равен: 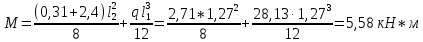 Сечение тавровое, расчётная ширина полки: 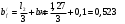 h0 = h – a = 200 – 35 = 165 мм (amin = 35мм) Расчёт арматуры: 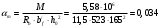 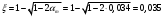 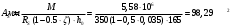 Принят 1Ø12 А400 с Аs = 113,1 мм2 (+13,1%). Продольные рёбра рассчитываются в составе всей плиты, рассматриваемой как балка П-образного сечения с высотой h= 400 мм и конструктивной шириной В1=1510 мм (номинальная ширина В=1,525 м). Толщина сжатой полки h′ƒ = 50 мм. Расчётный пролет при определении изгибающего момента принимается равным расстоянию между центрами опор на ригелях: l=lп– 100= 5750 – 100 = 5650 мм; расчетный пролет при определении поперечной силы: l0 = lп– 200= 5750 – 200=5550 мм, Нагрузка на 1 пог. м плиты (или на 1 пог. м двух продольных ребер) составит: - постоянная 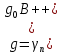 где 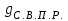 - расчётная нагрузка отсобственного веса трёх поперечных рёбер - расчётная нагрузка отсобственного веса трёх поперечных рёбер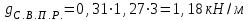 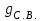 - расчётная нагрузка от собственного веса двух продольных рёбер с заливкой швов - расчётная нагрузка от собственного веса двух продольных рёбер с заливкой швов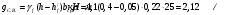 где: 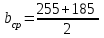 =220 мм - средняя ширина двух рёбер и шва; =220 мм - средняя ширина двух рёбер и шва; = 25 кН/м3- вес 1 м3 тяжелого железобетона. временная p= γn p0 B= 1,0 · 24· 1,525= 36,6 кН/м; полная q= g+ p= 9,59 + 36,6 = 46,19 кН/м; Усилия от расчетной нагрузки для расчёта на прочность 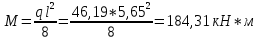 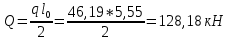 Расчет прочности нормальных сечений Продольная рабочая арматура в рёбрах принята в соответствии с заданием класса А400, расчётное сопротивление Rs=350 МПа (таблица Приложения «В»). Сечение тавровое с полкой в сжатой зоне представлено на рисунке 5; расчетная ширина полки b´f= B = 1525 мм; h′ƒ =50мм, h0 = h – a= 400 – 50 = 350 мм (а=50 мм при двухрядной арматуре). 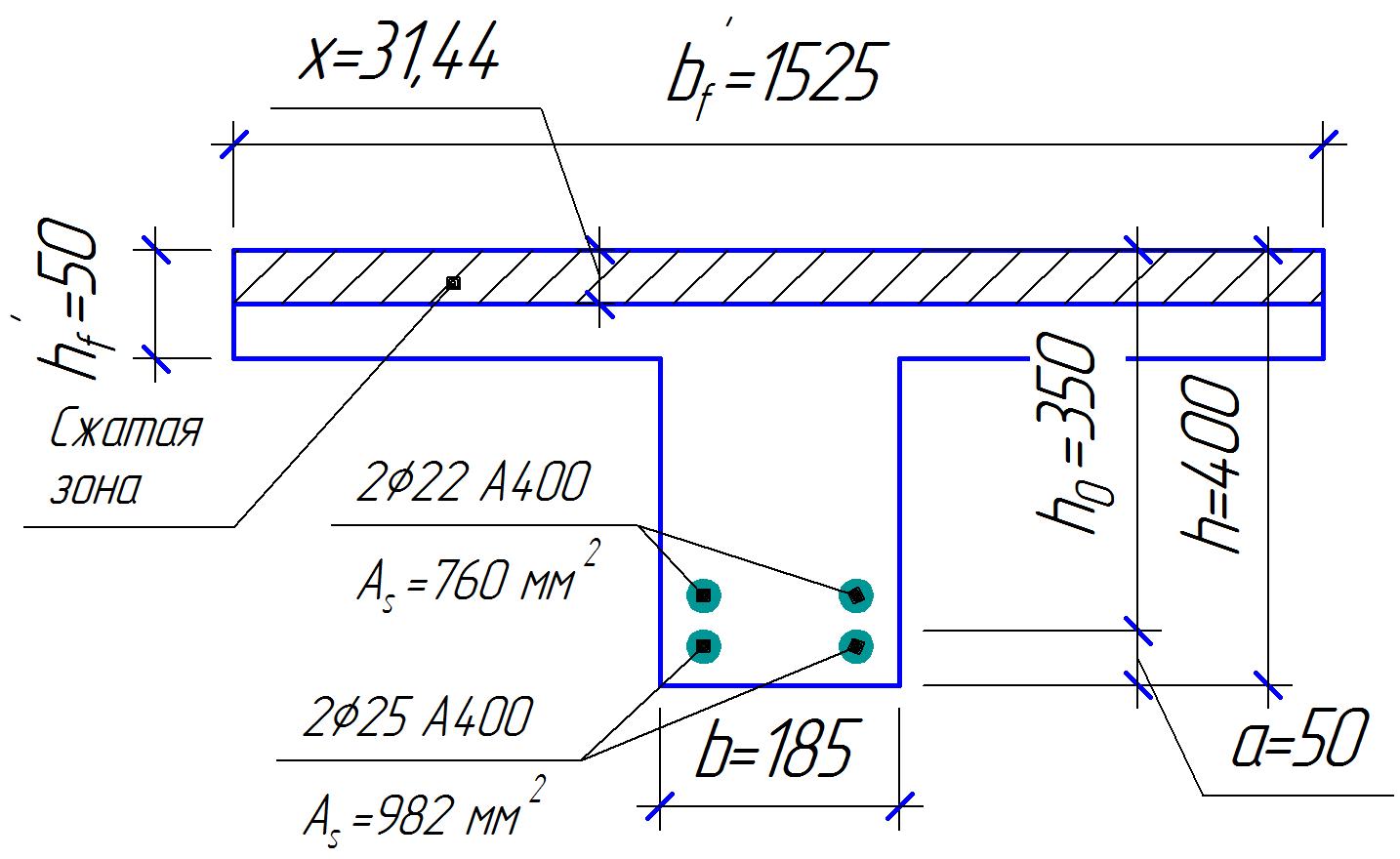 Рисунок 5 – Расчётное сечение продольного ребра по прочности Полагая, что нейтральная ось лежит в полке, αm и ξ будут равны: 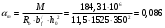 ; ;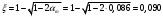 ; ;Проверка условия: x= h0 = 0,09 350 = 31,44 мм < hf=50 мм; 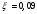 < < Площадь сечения продольной арматуры: 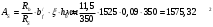 Принимаем продольную арматуру 222 +225 А400 с Аs= 1742 мм2 (+9,6%) по два стержня в каждом ребре. Расчёт нормальных сечений к продольной оси элемента по деформационной модели Расчет по прочности производят из условий: 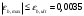 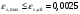 Деформации в продольной арматуре в предельном состоянии при двузначной эпюре деформаций согласно гипотезе плоских сечений равны: 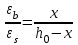 откуда, откуда, 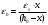 , ,где: х – фактическая высота сжатой зоны бетона:  где: х1 – высота сжатой зоны при прямоугольной эпюре напряжений, полученная при расчёте по предельным усилиям. Используя расчёты, выполненные выше (х1=31,44 мм, h0=350 мм), и задавшись 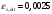 , проверим предельные деформации в бетоне: , проверим предельные деформации в бетоне: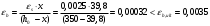 - деформации в бетоне не превышают предельных. - деформации в бетоне не превышают предельных.Расчет прочности наклонных сечений на поперечную силу Поперечная сила на грани опоры Qmax = 128,18 кН. В каждом продольном ребре устанавливается по одному каркасу с односторонним расположением двух рабочих стержней диаметром d= 25 мм (рис.3,5). Диаметр поперечных стержней из условия требований свариваемости должен быть не менее 0,25 диаметра продольной арматуры. В данном случае принимаем поперечные стержни диаметром dsw= 8 мм > 0,25∙25 = 6,25 мм из арматуры класса А240, Asw1=50,3 мм2; расчетное сопротивление Rsw= 170 МПа. При Asw1=50,3 мм2 и n= 2 (на оба ребра) имеем: Asw = nAsw1=250,3 = 100,6 мм2. Бетон тяжелый класса В20 (Rb = 11,5 МПа; Rbt = 0,9 МПа; коэффициент условий работы бетона γb1=1,0 т.к. кратковременная нагрузка составляет более 10% от всей временной нагрузки). Предварительно принятый шаг хомутов: Sw1 = 125 мм (Sw1 ≤ 0,5h0 = 0,5 ∙ 350 = 175мм; Sw1≤300мм) Sw2= 250 мм (Sw2 ≤ 0,75h0= 0,75 ∙ 350 = 262,5мм;Sw2≤500мм) Прочность бетонной сжатой полосы из условия: 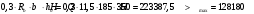 , то есть прочность полосы обеспечена. , то есть прочность полосы обеспечена.Интенсивность хомутов определяется по формуле (13) [10]: 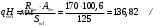 Поскольку qsw1 = 136,82 Н/мм >0,25Rвt·b = 0,250,9185 =41,6 Н/мм - хомуты полностью учитываются в расчете и значение Мb определяется по формуле: 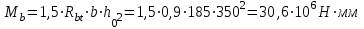 Самая невыгодная длина проекции наклонного сечения C определяется из выражений: 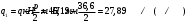 Поскольку 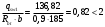 , значение С определяется по формуле: , значение С определяется по формуле: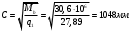 < 3h0=3350=1050 мм, < 3h0=3350=1050 мм,ПринятоС = 1048 мм. Длина проекции наклонной трещины С0 принимается не более С и не более 2h0. В данном случае с0 = 2h0 = 2 350 = 700 мм. Тогда  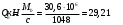 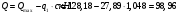 . .Проверяем условие (8) [10]: 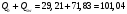 кН > кН >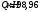 (+2,1%), (+2,1%),т.е. прочность наклонных сечений обеспечена, увиличить шаг мы не можем т.к.Sw1 = 125 мм (Sw1 ≤ 0,5h0 = 0,5 ∙ 350 = 175мм . Проверка требования: 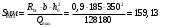 > Sw1=100 мм. > Sw1=100 мм.т.е. требование 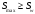 выполнено. выполнено.Определение длины приопорного участка А. Аналитический метод. При равномерно распределённой нагрузке длина приопорного участка определяется в зависимости от: 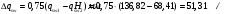 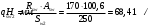 Так какΔqsw=51,31 Н/мм > q1=27,89 Н/мм, длина приопорного участка определится по формуле: 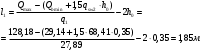 где: Qb,min = 0,5Rbtbh0 = 0,5∙0,9∙185∙350 =29,14 кН Б. Графический метод.  Рисунок 6 - К определению l1 графическим методом Длина приопорного участка l1 принимается большая из двух значений, то есть по рисунку 6 l1 = 2,15 м. |
