жбк курсовая. Курсовая работа Расчёт сборных железобетонных конструкций многоэтажного производственного здания Студент гр. 181 Сильченко М. К
 Скачать 5.32 Mb. Скачать 5.32 Mb.
|
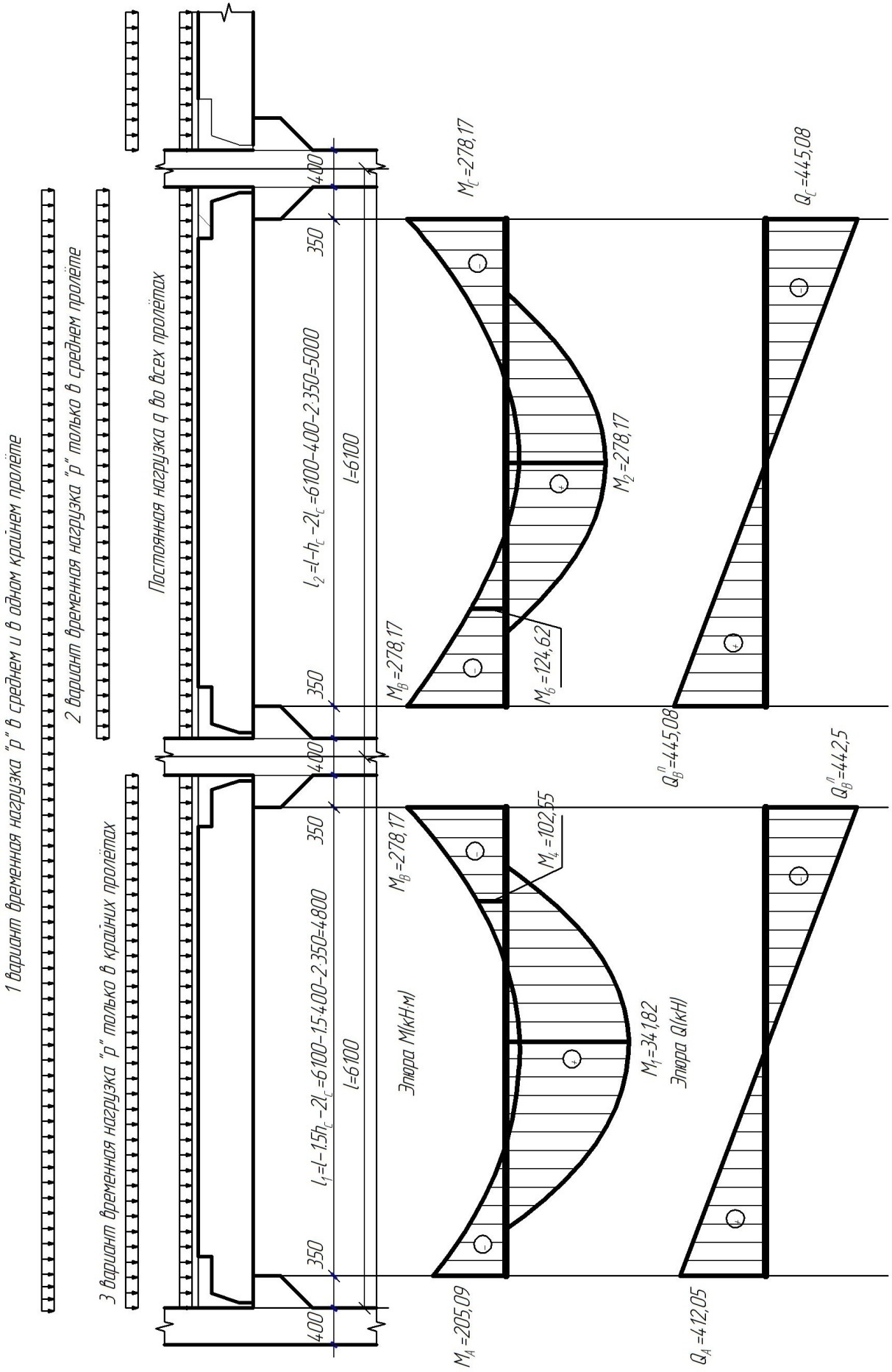
1.3.3 Расчёт плиты по прогибамПолная кривизна для участков с трещинами в растянутой зоне определяется по формуле 7.3.8 [4]: 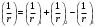 , а полный прогиб плиты: , а полный прогиб плиты:  где: где: 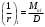 - кривизна от продолжительного действия постоянной и длительной нагрузки - кривизна от продолжительного действия постоянной и длительной нагрузкиИз расчёта acrc1: Ebred =Eb1= 6818,18 МПа, αs1 = 29,33, xm = 147,24 мм. 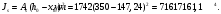 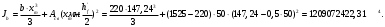 Момент инерции приведённого сечения без учёта растянутого бетона: 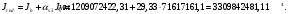 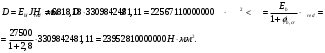 где: 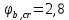 - коэффициент ползучести бетона для бетона В20. - коэффициент ползучести бетона для бетона В20.Принято: 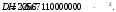 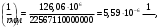 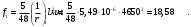 Кривизна от непродолжительного действия всей нагрузки: 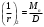 , где Мn =156,49 кН∙м , где Мn =156,49 кН∙мИз расчёта acrc2: Ebred =Eb1= 10000 МПа, αs2 = 20,0, xm = 121,82 мм. 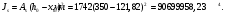 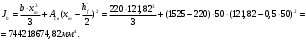 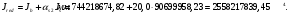 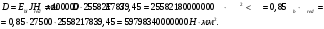 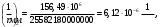 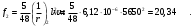 Кривизна от непродолжительного действия постоянной и длительной нагрузки: 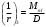 , где Mnl = 126,06 кН∙м , где Mnl = 126,06 кН∙мИз расчёта acrc2, (так как нагрузка носит непродолжительный характер): Ebred =Eb1= 10000 МПа, αs2 = 20,0, xm = 121,82 мм, 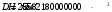 . .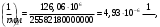   Плита удовлетворяет требованиям таблицы 19 [2]: а) эстетико-психологическим  б) конструктивным  Вывод: плита удовлетворяет требованиям по второй группе предельных состояний. 2. Расчёт сборного ригеля поперечной рамыДля сборного железобетонного перекрытия, план и разрез которого представлены на рис. 1, требуется рассчитать сборный ригель, используя данные и результаты расчёта плиты. Сетка колонн llк = 6,1 х6,2 м. Для ригеля среднего пролета необходимо построить эпюры моментов от нагрузки и его несущей способности. Армирование ригеля представлено на рисунке 8: ригель с двумя продольными каркасами и двух рядным расположение стержней. 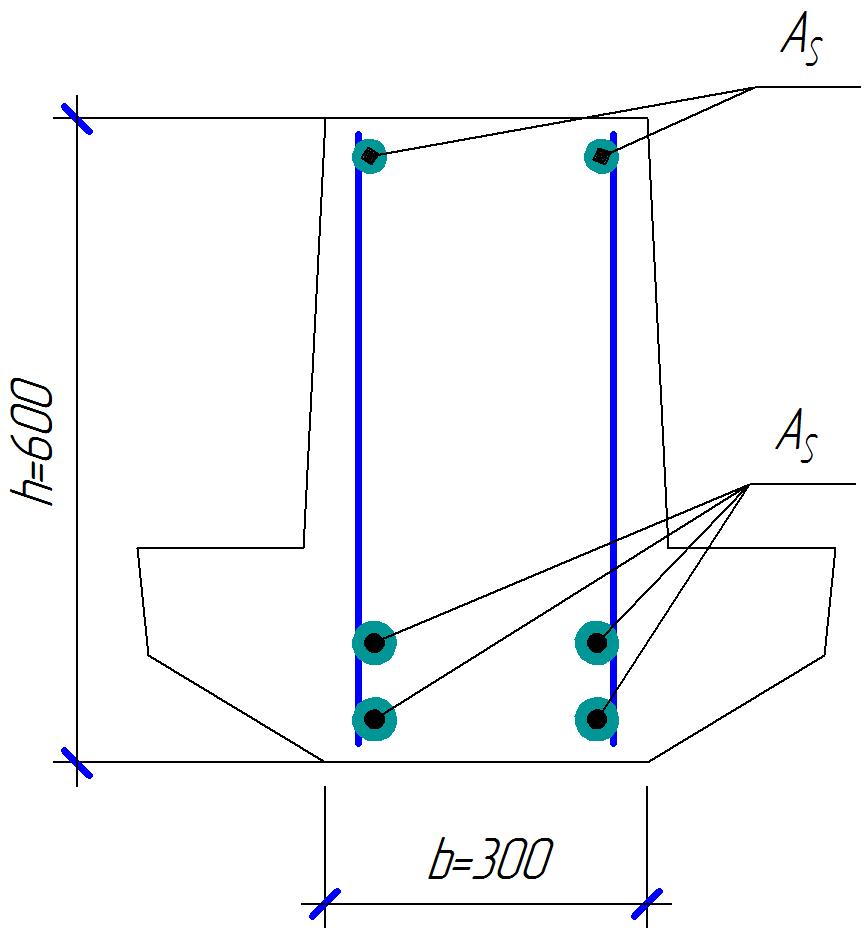 Рисунок 8 – Поперечное сечение ригеля 2.1 Вариант ригеля с двумя каркасамиДанные для расчёта: бетон тяжелый, класс бетона B15, коэффициент работы бетона γb1 = 1,0. Расчётные сопротивления бетона с учетом γb1 = 1,0 равны: Rb = 1,0∙8,5 = 8,5 МПа; Rbt = 1,0∙0,75 = 0,75 МПа. Продольная и поперечная арматура – класса A500. Коэффициент снижения временной нагрузки к1 = 0,9. 2.1.1 Расчётные нагрузкиНагрузка на ригель собирается с грузовой полосы (представленной на рисунке 1) шириной lк = 6,2 м, равной расстоянию между осями ригелей (по lк/2 с каждой стороны от оси ригеля). а) постоянная нагрузка (с γn = 1,0 и γƒ = 1,1): вес железобетонных плит с заливкой швов gn = 3,0кН/м2 принят по данным типовой серии ИИ 24-1 данных плит: 1,0∙1,1∙3,0∙6,2 = 20,46 кН/м; вес пола и перегородок: 1,0∙1,1∙2,5∙6,2 = 17,05 кН/м; собственный вес ригеля с приведённой шириной b = 0,4м и высотой h = 0,6 м (размеры предварительные) 1,0∙1,1∙0,4∙0,6∙25 = 6,6 кН/м; Итого постоянная нагрузка g = 44,11 кН/м. б) Временная нагрузка с коэффициентом снижения к1 = 0,9, γn = 1,0 и γƒ = 1,2: p = 1,0∙0,9∙1,2∙20∙6,2 = 133,92 кН/м. Полная расчетная нагрузка: q = g + p= 44,11+ 133,92 = 178,03 кН/пм. 2.1.2 Расчётные пролёты ригеляПри поперечном сечении колонн 400400 мм (hc = 400 мм) и вылете консолей lc = 350 мм расчётные пролёты ригеля равны (см. рис. 9): крайний пролет l1 = l – 1,5hc - 2lc = 6,1 – 1,5*0,4 – 2 ∙ 0,35 = 4,8 м. средний пролет l2 = l - hc - 2lc = 6,1 – 0,4 – 2 ∙ 0,35 = 5,0 м. 2.1.3 Расчетные изгибающие моментыВ крайнем пролёте: 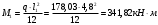 На крайней опоре: 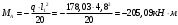 В средних пролетах и на средних опорах: 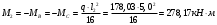 Отрицательные моменты в пролетах при p/g = 133,92/ 44,11= 3,04: в крайнем пролёте для точки «4» при β = -0,025 M4=β (g+p) l12 = -0,025∙178,03∙4,8 2 = - 102,55 кН∙м. в среднем пролёте для точки «6» при β = -0,028 M6=β (g+p) l22 = -0,028∙178,03∙5,0 2 = - 124,62 кН∙м.
2.1.4 Расчетные поперечные силыПоперечная сила в каждом пролёте определяется как для простой балки с опорными моментами на концах. На крайней опоре: 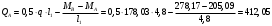 кН кННа опоре B слева: 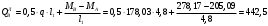 кН кННа опоре B справа и на средних опорах: 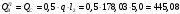 кН кН2.1.5 Расчет ригеля на прочность по нормальным сечениямДля арматуры класса A500 ξR = 0,493 . Ширина сечения ригеля b = 300мм. Высота ригеля определяется по моменту в крайнем пролёте 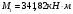 , задаваясь значением ξ = 0,35 < ξR = 0,493. Откуда αm = ξ (1 – 0,5ξ) = 0,35(1 – 0,5∙0,35) = 0,289. Сечение рассчитывается как прямоугольное по формуле: , задаваясь значением ξ = 0,35 < ξR = 0,493. Откуда αm = ξ (1 – 0,5ξ) = 0,35(1 – 0,5∙0,35) = 0,289. Сечение рассчитывается как прямоугольное по формуле: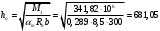 мм ммh = h0+a = 585,5 + 70 = 751,05 мм; принимаем h = 600 мм (hпл+ 200мм), что соответствует предварительно принятой величине. Пересчёт нагрузки и усилий не требуется. Расчёт арматуры Расчётное сопротивление арматуры класса A500 Rs = 435 МПа а) Крайний пролёт. M1 = 341,82 кН∙м; b = 300 мм; h= 600 мм; а=70 мм (предварительно), тогда h0 = h - a = 600 – 70 = 530 мм. Расчётное сечение представлено на рисунке 10. 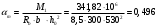 ; ;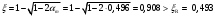 , т.к. ξ> ξR и разрушение произойдет по сжатой зоне бетона, что недопустимо! Принимаем бетон класса В20. Rb = 1,0∙11,5 = 11,5 МПа; Rbt = 1,0∙0,9 = 0,9 МПа. , т.к. ξ> ξR и разрушение произойдет по сжатой зоне бетона, что недопустимо! Принимаем бетон класса В20. Rb = 1,0∙11,5 = 11,5 МПа; Rbt = 1,0∙0,9 = 0,9 МПа.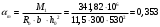 ; ;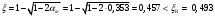  Принято 4Ø25A500 с АS = 1963 мм2 (+2,1%). a = 30+27/2+60/2 = 73,5 мм (где 30мм - толщина закладной детали, к которой привариваются продольные стержни; 60мм - расстояние между стержнями диаметром 25 мм принимается по приложению К; 27 мм диаметр арматуры 25 по рифам принимается по приложению И), пересчёт а не требуется. б) Крайняя опора. MA= -205,09кН∙м;b = 300 мм; h = 600 мм; а=65 мм (предварительно), тогда h0 = h - a = 600 – 65 = 535 мм (арматура расположена в один ряд по высоте). 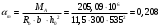 ; ;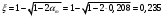 ; ;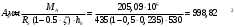 принято 228 A500 с As = 1232 мм2 (+18,9%). В этом случае h0 = h - a = 600 – (80 – d/2) = 600 – (80 – 30/2) = 535 мм (где 80мм - расстояние от верха ригеля до низа арматурного стержня), что соответствует предварительно принятому. в) Верхняя пролетная арматура крайнего пролета по моменту в сечении «4» M4 = -102,55 кН∙м; h0 = h - a = 600 - 65 = 535 мм (однорядная арматура). 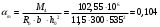 ; ;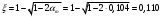 ; ;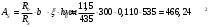 принято 218 A400 с As= 509 мм2 (+8,4 %), принято 218 A400 с As= 509 мм2 (+8,4 %), 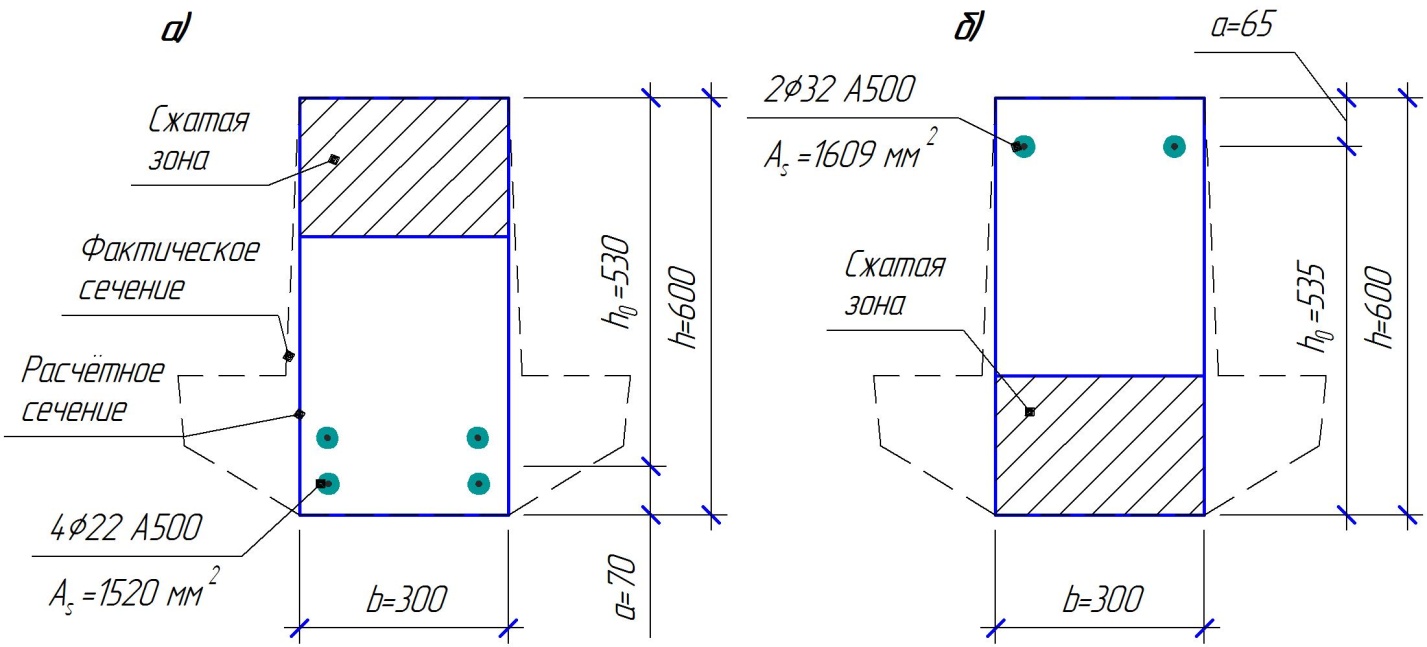 Рисунок 10–Расчётные сечения среднего ригеля в пролёте (а) и на опоре В (б) г) Средний пролет. MB= MC= M2= 278,17 кН∙м; b = 300 мм; h= 600 мм; а=70 мм (предварительно), тогда h0 = h - a = 600 – 70 = 530 мм 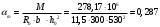 ; ;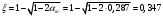 ; ; принято 422 A500 с As = 1520 мм2 (+3,9 %). д) Средняя опора. M2 =MВ= MС= 278,17 кН∙м; b = 300 мм; h= 600 мм; а=65 мм тогда h0 = h - a = 600 – 65= 535 мм (арматура расположена в один ряд по высоте). 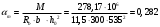 ; ;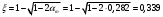 ; ;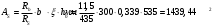 принято 232 A500 с As = 1609 мм2 (+10,5 %). е) Верхняя пролётная арматура среднего пролета по моменту в сечении «6» M6 = -124,62 кН∙м; b = 300 мм; h = 600 мм; h0 =h - a = 600-65=535мм (однорядная арматура). 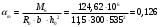 ; ;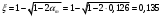 ; ;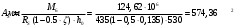 принято 220 A500 с As= 628 мм2 (+8,5%), 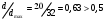 2.1.6 Определение площади поперечного сечения поперечной арматуры на отрывНагрузка на ригель приложена в пределах высоты его сечения. Поэтому необходима дополнительная вертикальная (поперечная) арматура, площадь которой определяется расчётом на отрыв. Отрывающая нагрузка, приходящаяся на 1пм длины ригеля и передающаяся через его полки на среднюю часть равна (без учёта нагрузки от собственного веса ригеля и нагрузки на его ширине равной 0,3м):  где: 0,3м - ширина поперечного сечения ригеля. 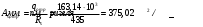 Так как шаг поперечных хомутов Swменьше 1000 мм, площадь 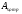 будет уменьшаться пропорционально будет уменьшаться пропорционально 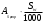 2.1.7 Расчет среднего ригеля на прочность по наклоннымсечениям на действие поперечных силВ крайнем и средних пролетах ригеля устанавливаются по два плоских сварных каркаса с односторонним расположением рабочих продольных стержней. Наибольший диаметр продольных стержней в крайнем и среднем пролёте в данном примере Ø 32 мм. Для обеспечения требованиям качественной сварки минимальный диаметр поперечных стержней будет равен в крайнем и среднем пролёте Ø 8мм. Средний пролет 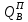 = 445,08 кН, h = 600 мм, h0 = 535 мм. = 445,08 кН, h = 600 мм, h0 = 535 мм.Предварительно принято dsw = 8мм, Sw1 = 50мм (Sw1≤ 0,5 h0; Sw1 ≤ 300 мм). Класс арматуры А 240. Проверка прочности наклонной сжатой полосы QA = 318,4 кН<0,3∙Rb∙b∙h0=0,3∙11,5∙300∙535 = 553,73 кН - прочность сжатой полосы обеспечена Проверка прочности наклонного сечения 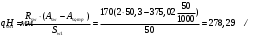 Поскольку qsw1=278,29 Н/мм > 0,25Rbtb = 0,25∙0,9∙300 = = 67,5 Н/мм - хомуты не учитываются в расчете и Мb определяется по формуле: 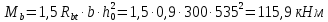 q1 = g + p/2 = 44,11 + 133,92/2 = 111,07 кН/м Поскольку 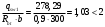 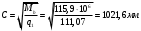 < 3h0=3*535=1605 мм, < 3h0=3*535=1605 мм,Принято: С1 = 1021,6 мм; С01 = 2h0 = 2∙535 = 1070мм 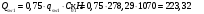 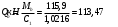 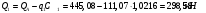 Проверка условия 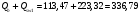 кН > кН >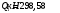 (+11,3%), (+11,3%),Прочность наклонного сечения обеспечена, уменьшение запаса несущей способности путём увеличения Sw до 75мм невозможно, так как прочность наклонного сечения становиться меньше действующего усилия. 2.1.8 Определение длины приопорных участков крайнего ригеляА. Аналитический метод При равномерно распределённой нагрузке длина приопорного участка определяется в зависимости от: 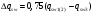 где: qsw3 - погонное усилие, воспринимаемое поперечными стержнями в середине пролёта изгибаемого элемента (ригеля). Приопорный участок у опоры А: Шаг поперечных стержней в середине пролёта Sw3 принимается по конструктивным соображениям п. 5.21 [5], но не более 0,75h0 и 500мм. В данном случае предварительно принятdsw3 = 8мм,Sw3 = 250мм (Sw3≤ 0,75 h0 = 0,75∙535 = 397,5 мм; Sw3 ≤ 500 мм), арматура класса А400. 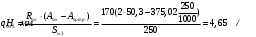 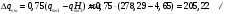 Так какΔqsw=205,22 Н/мм > q1=111,07 Н/мм, длина приопорного участка определится по формуле: 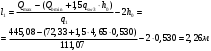 где: Qb,min = 0,5Rbtbh0 = 0,5∙0,9∙300∙530 =72,33кН Б. Графический метод 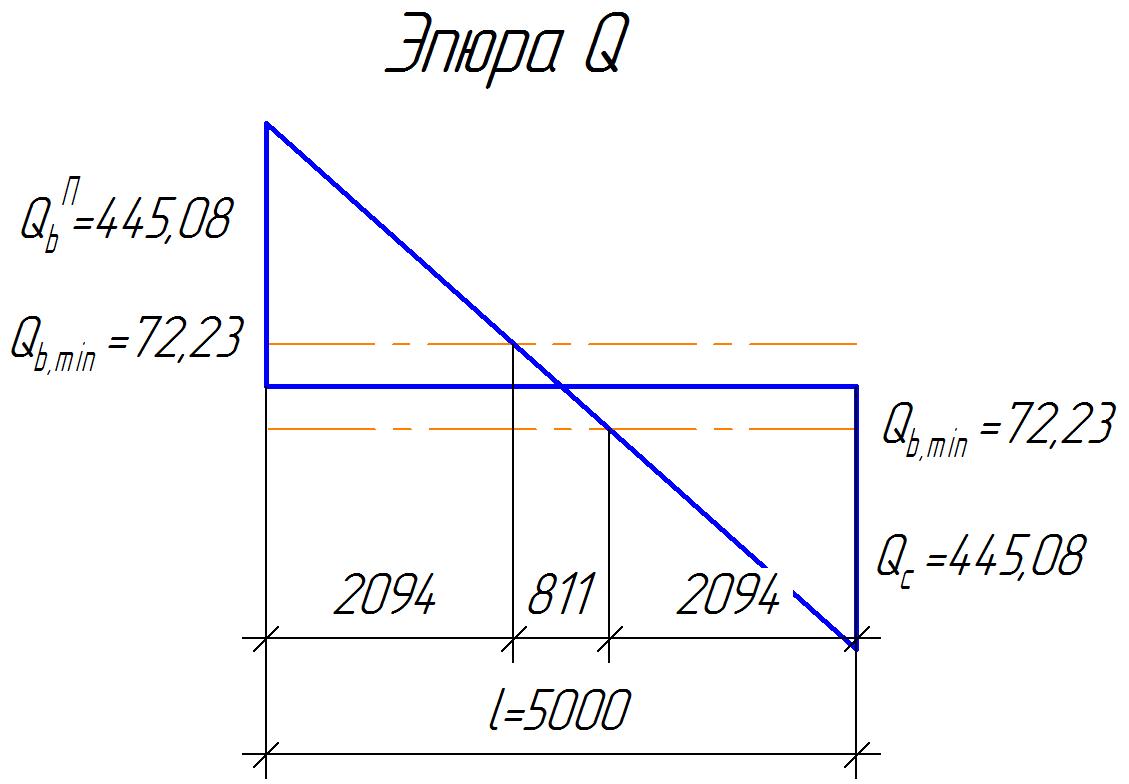 Рисунок 11 - К определению l1 графическим методом в среднем ригеле Длина приопорного участка l1 принимается по большему значению, то есть 2260 мм 2.1.9 Обрыв продольной арматуры в среднем ригеле.Построение эпюры несущей способности ригеляВ целях экономии до 50% продольной арматуры её можно обрывать там, где она уже не нужна. Для определения места обрыва продольной арматуры строится огибающая эпюра изгибающих моментов от внешних нагрузок и эпюра несущей способности сечений ригеля Mult. Моменты от внешней нагрузки в пяти точках огибающей эпюры определяются по формуле: 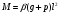 Расчётные моменты эпюры несущей способности в каждом сечении равны: 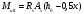 где: где: 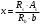 As - площадь арматуры в рассматриваемом сечении ригеля. Место фактического обрыва стержней отстаёт от теоретического на расстояние W, принимаемое не менее величины:  , при этом, если , при этом, если 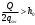 , ,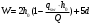 где: Q, qsw и d- соответственно поперечная сила, поперечное усилие в поперечных стержнях и диаметр обрываемого стержня в месте его теоретического обрыва. По всей длине ригеля должно соблюдаться условие: 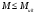 . .Подсчёт моментов при отношении p/g = 133,92 / 44,11 = 3,04. q=178,03 кН/м сведён в таблицу 1. Нулевые точки эпюры положительных моментов располагаются на расстоянии 0,1l2 = 0,5м от грани левой опоры и 0,125l2 = 0,625м от грани правой опоры. Таблица 1 - Изгибающие моменты М в крайнем пролете
На положительный момент М2 = 278,17 кН∙м в п.2.1.5а была принята арматура 4Ø22А500 с As = 1520 мм2; h0=530 мм. 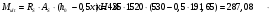 где: 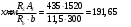 Ввиду убывания положительного момента к опорам 222 А500 обрываются в пролёте. Момент Мult, отвечающий оставшейся 222 А500 будет равен: h0=h-30-d/2=600-30-24/2=558 мм (24 мм – диаметр арматуры 22 по рифам, приложение И) 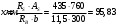 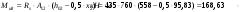 На отрицательный опорный момент на опоре MВ =MС =-278,17 кН∙м в п.2.1.5 приняты 2Ø32А500 с As = 1609мм2; h0=535 мм. 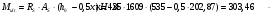 где: 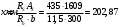 В сечении «6» М6 = -124,62 кН∙м; арматура 2Ø20 А500 с Аs = 628мм2; h0 = 535мм 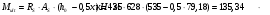 где: 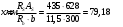 Обрываемые опорные стержни заводятся за место теоретического обрыва на величину W. Расстояние от опорных стержней до мест теоретического обрыва стержней а(1,2) и значение Q(1,2) определяется из эпюры графически по рисунку 12. Из расчёта ригеля на прочность по поперечной силе п. 2.1.7 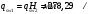 , , h01=530, h02=535 мм. , , h01=530, h02=535 мм.Значения W будут (см. рис.12): для пролетных стержней слева 2Ø22 А500: 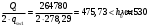 , поэтому , поэтому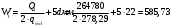 для надопорных стержней 232 A500 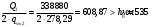 , поэтому , поэтому 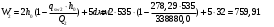 Принято W1=590 мм; W2=760 мм, 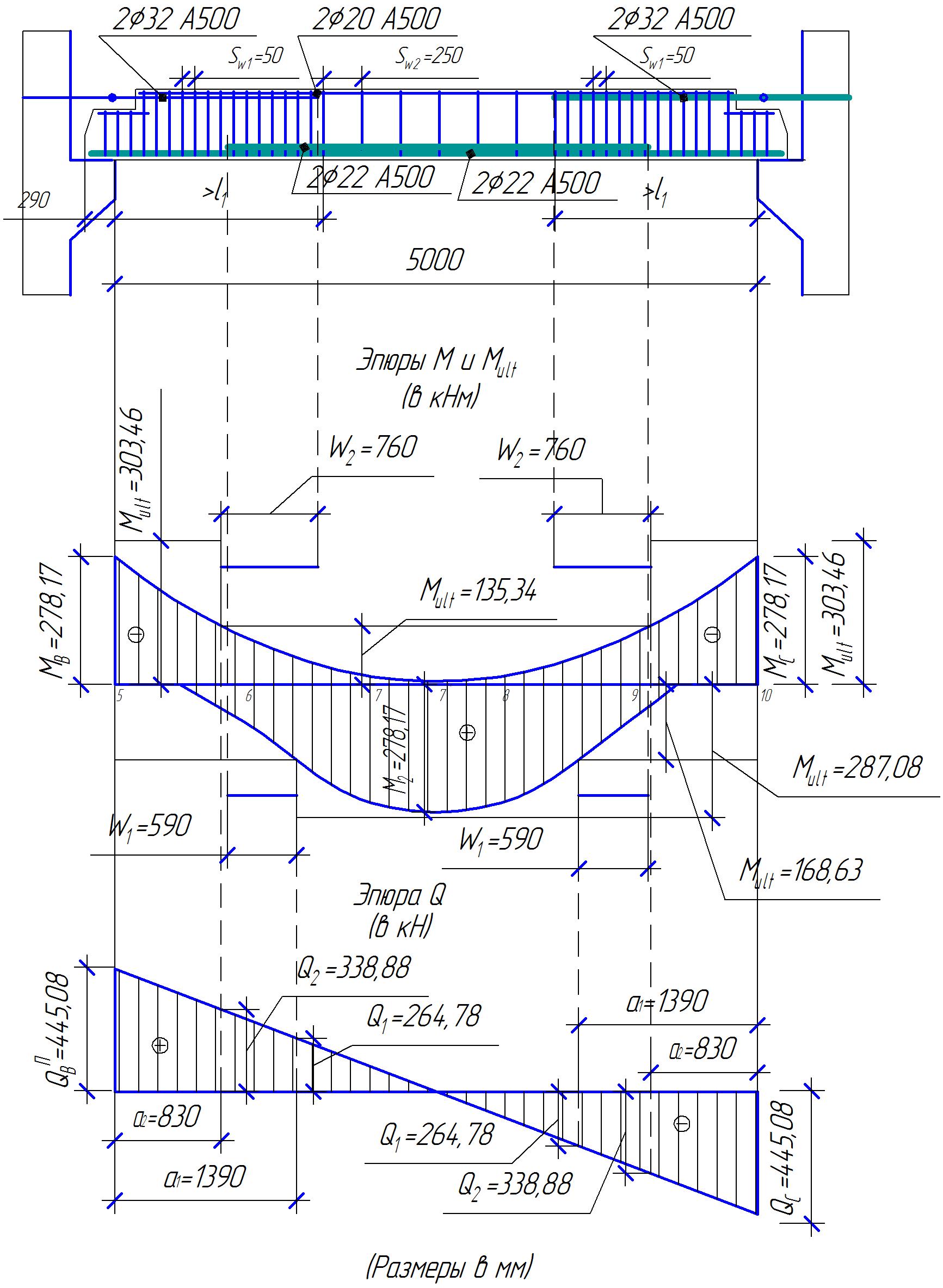 Рисунок 12- Огибающая эпюра моментов и «эпюра арматуры» крайнего ригеля | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||