ТОЭ Курсовая 3 вариант. Тоэ Курсовая 3 вариант. Курсовая работа студент гр. Проверил Елисеев С. Н. Москва 2021 г. Оглавление Задание 1 3 Введение 3
 Скачать 1.17 Mb.
|
Метод узловых потенциаловС помощью метода узловых потенциалов определим токи во всех ветвях. Произвольно выбираем направление всех токов в ветвях на исходной схеме (рис.5): 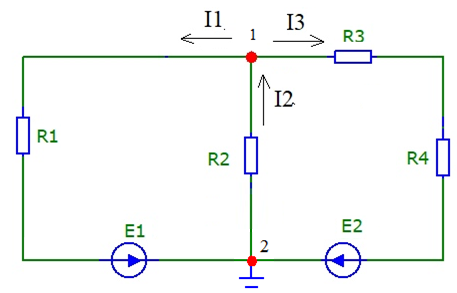 Рисунок 5 - Схема с направлениями токов Число уравнений:  Принимаем потенциал узла 2 равен нулю:  . Тогда составим уравнение для нахождения потенциала узла 1:  Где  – потенциал узла 1; - сумма проводимостей ветвей, сходящихся в узле 1; - сумма проводимостей ветвей, непосредственно соединяющих узел 1 с узлом 2; – алгебраическая сумма произведения ЭДС ветвей, примыкающих к узлу 1, на их проводимости.С помощью программы Mathcad находим: 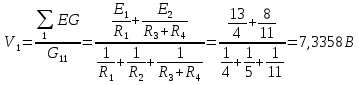 Найдя потенциал V1 подставим его в уравнения для токов и получим значения всех токов с помощью программы Mathcad. Токи в ветвях, согласно обобщенному закону Ома, при V2=0 В равны:    Ответ:  ;  ;  Метод двух узловС помощью двух узлов определим токи во всех ветвях. Метод двух узлов является частным случаем метода узловых потенциалов и наиболее рационален для расчёта цепей, содержащих два узла. Для расчёта методом двух узлов находят напряжение между этими узлами U12. Нужно определить напряжение между двух узлов и рассчитать исходя из этого все токи в ветвях. Схема с учётом данного метода представлена на рис. 6: 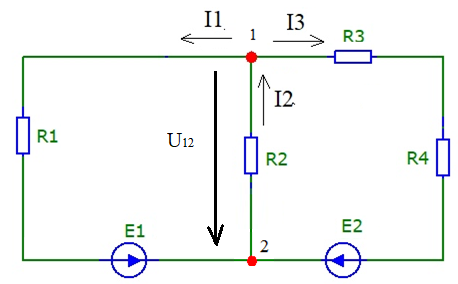 Рисунок 6 - Схема для метода 2 узлов Примем потенциал узла 2 равным нулю V2=0 В. Тогда напряжение U12 будет направлено из точки с большим потенциалом, к точке с меньшим. 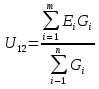 ,где  - алгебраическая сумма произведения ЭДС ветвей, примыкающих к узлу 1, на их проводимости; - алгебраическая сумма проводимостей всех ветвей схемы.Определяем напряжение U12 между узлами по формуле: 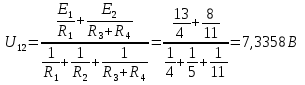 Знак ЭДС определяется ее направлением. Если к узлу, то отрицательное, если от узла - положительное. С помощью программы MathCad получаем значения всех токов:    Ответ: ; ; |