ТОЭ Курсовая 3 вариант. Тоэ Курсовая 3 вариант. Курсовая работа студент гр. Проверил Елисеев С. Н. Москва 2021 г. Оглавление Задание 1 3 Введение 3

• Название: Курсовая работа студент гр. Проверил Елисеев С. Н. Москва 2021 г. Оглавление Задание 1 3 Введение 3
• Анкор: ТОЭ Курсовая 3 вариант
• Дата: 11.11.2021
• Размер: 1.17 Mb.
• Имя файла: Тоэ Курсовая 3 вариант.docx
• Тип: Курсовая; #269270
• страница: 7 из 8

2.2. Метод контурных токов

Для использования метода контурных токов необходимо произвольно задать положительные направления токов во всех ветвях цепи, а также положительные направления контурных токов, что продемонстрировано на рисунке 26: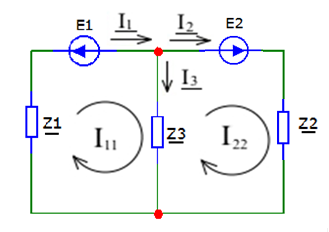



Рисунок 26 - Схема с положительными направлениями токов

Рассчитываем необходимое количество уравнений по 2-му закону Кирхгофа:



- количество ветвей;

- количество узлов

Для каждого контура запишем уравнение относительно контурных токов:















Составим систему и решим ее: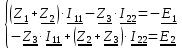







Данная система в эквивалентной матричной форме: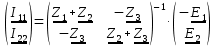



Вычисление на компьютере с помощью программы Mathcad: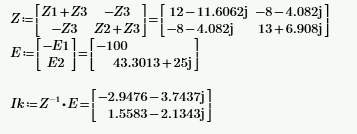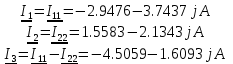





Ответ: ; ; .

2.3. Метод узловых потенциалов

Произвольно выбираем направление всех токов в ветвях на исходной схеме рисунок 27: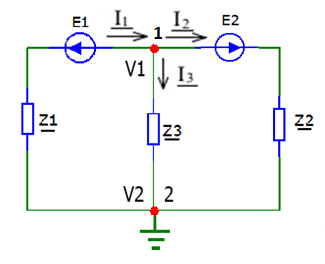



Рисунок 27 - Схема с направлениями токов

Число уравнений:



Принимаем потенциал узла 2 равен нулю: V₂ = 0 В. Тогда составим уравнение для нахождения потенциала узла 1:

,

где V₁ – потенциал 1 узла;

– сумма проводимостей ветвей, сходящихся в узле 1;

– алгебраическая сумма произведения ЭДС ветвей, примыкающих к узлу 1, на их проводимости.

Рассчитаем с помощью программы Mathcad: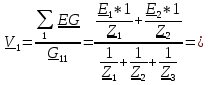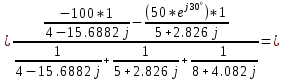







Найдя потенциал V₁, подставим его в уравнения для комплексных токов и получим значения всех комплексных токов с помощью программы Mathcad. Токи в ветвях, согласно обобщенному закону Ома, при V₂ = 0 В 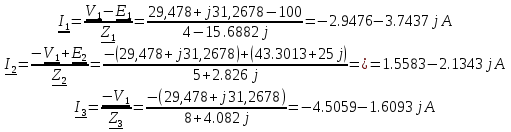равны:



Ответ: ; ; .