ТОЭ Курсовая 3 вариант. Тоэ Курсовая 3 вариант. Курсовая работа студент гр. Проверил Елисеев С. Н. Москва 2021 г. Оглавление Задание 1 3 Введение 3

• Название: Курсовая работа студент гр. Проверил Елисеев С. Н. Москва 2021 г. Оглавление Задание 1 3 Введение 3
• Анкор: ТОЭ Курсовая 3 вариант
• Дата: 11.11.2021
• Размер: 1.17 Mb.
• Имя файла: Тоэ Курсовая 3 вариант.docx
• Тип: Курсовая; #269270
• страница: 8 из 8

Метод двух узлов

Метод двух узлов является частным случаем метода узловых потенциалов и наиболее рационален для расчёта схем с двумя узлами. Схема с учётом данного метода представлена на рисунке 28: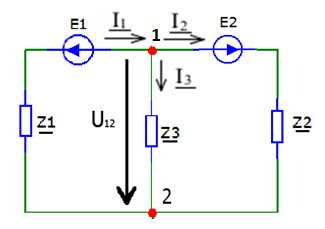



Рисунок 28 - Схема для метода 2 узлов

Примем потенциал узла 2 равным нулю V₂ = 0 В. Тогда напряжение U₁₂ будет направлено из точки с большим потенциалом, к точке с меньшим.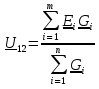

, где

– алгебраическая сумма произведения ЭДС ветвей, примыкающих к узлу 1, на их проводимости G_i = 1/Z_i;

– арифметическая сумма проводимостей всех ветвей схемы

Определяем напряжение U₁₂ между узлами по формуле: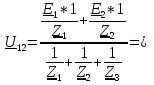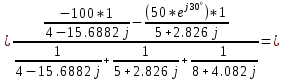







Подставим значения в формулу для расчета тока: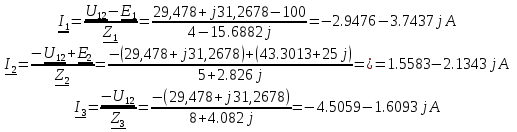



Ответ: ; ; .

4. Метод наложения

Рассчитаем все комплексные токи в цепи методом наложения. Произвольно выбираем направления комплексных токов в цепи. Схема представлена на рисунке 29: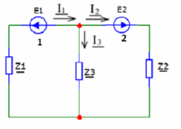



Рисунок 29 - Схема с направлениями комплексных токов

Положить равными нулю все источники ЭДС и тока кроме второго. При этом независимые источники, ЭДС которых равны нулю, заменяем короткозамкнутыми отрезками. Для удобства частичные токи будем обозначать штрихами. Исходная схема представлена на рис. 30: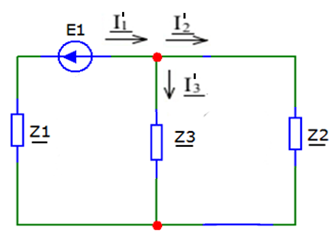



Рисунок 30 - Схема с источниками тока = 0, кроме 2

В полученной схеме с одним независимым источником E2 рассчитаем все частичные токи методом конутрных токов:

Z₁₁I'₁₁ + Z₁₂I'₂₂ = E₁₁

Z₁₂I'₁₁ + Z₂₂I'₂₂ = E₂₂

где

Z₁₁ = Z₁ + Z₃ – сумма сопротивлений всех ветвей контура 1, т.е. собственное сопротивление контура 1;

Z₂₂ = Z₂ + Z₃ – сумма сопротивлений всех ветвей контура 2, т.е. собственное сопротивление контура 2;

Z₁₂ =Z₂₁ = - Z₃ – общее сопротивление контуров 1 и 2;

I'₁₁ - контурный ток первого контура;

I'₂₂ - контурный ток второго контура;

E₁₁ = -E₁– алгебраическая сумма ЭДС контура 1;

E₂₂ =0– алгебраическая сумма ЭДС контура 2.

С помощью программы Mathcad, найдем контурные токи I’₁₁ и I’₂₂:

I'₁₁ = А

I'₂₂ = А

I'₃ = I'₁₁ -I'₂₂ = А

Пусть источник ЭДС E2 отключён. Методом контурных токов найдем частичные токи.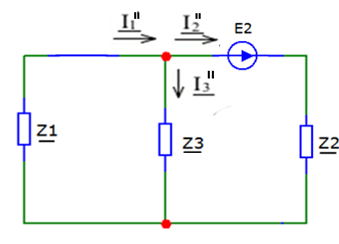



Рисунок 31 - Схема с частичными токами

Z₁₁I''₁₁ + Z₁₂I''₂₂ = E₁₁

Z₁₂I''₁₁ + Z₂₂I''₂₂ = E₂₂

где

Z₁₁ = Z₁ + Z₃ – сумма сопротивлений всех ветвей контура 1, т.е. собственное сопротивление контура 1;

Z₂₂ = Z₂ + Z₃ – сумма сопротивлений всех ветвей контура 2, т.е. собственное сопротивление контура 2;

Z₁₂ =Z₂₁ = -Z₃ – общее сопротивление контуров 1 и 2;

I''₁₁ - контурный ток первого контура;

I''₂₂ - контурный ток второго контура;

E₁₁ = 0 – алгебраическая сумма ЭДС контура 1;

E₂₂ = E₂ – алгебраическая сумма ЭДС контура 2;

С помощью программы Mathcad, найдем контурные токи I''₁₁ и I''₂₂:

I’'₁₁ = А

I’'₂₂ = А

I’'₃ = I'₁₁ -I'₂₂ = А

Токи ветвей находятся по формулам с помощью программы Mathcad:







Ответ: ; ; .

4. Метод эквивалентного генератора ЭДС

Произвольно выбираем положительное направление искомого тока I₁ в ветви на исходной схеме. Исходная схема 1 представлена на рисунке 32: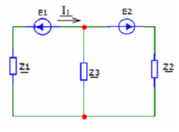



Рисунок 32 - Схема с выбранным направлением

Составим схему 2, исключив ветвь, по которой течет искомый ток. Данная схема представлена на рисунке 33: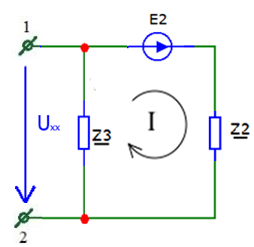



Рисунок 33 - Схема с исключённой ветвью

Для расчета найдем ток по закону Ома для замкнутого контура:





Схема для расчета 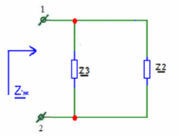. В схеме 2 заменим все источники ЭДС на короткозамкнутые отрезки:



Рисунок 34 - Схема с короткозамкнутыми отрезками



И последний этап в этом методе: составляем схему, изображающую одноконтурную цепь с ветвью, исключенной при составлении схемы 2. Направление E_эк принимаем противоположным направлению U_xx.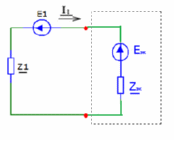



Рисунок 35 - Схема одноконтурной цепи



Ответ:

Кривая изменений комплексного тока во времени (рис.36):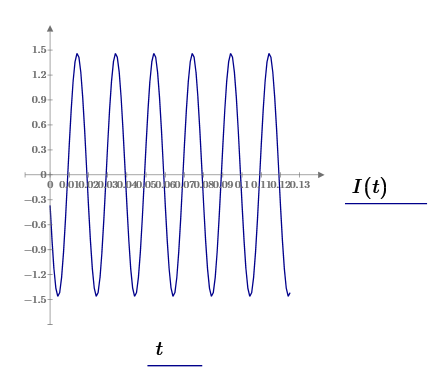



Рисунок 36

4. Метод эквивалентного генератора тока

Произвольно выбираем положительное направление искомого тока I₃ в ветви. Исходная схема 1 представлена на рисунке 37: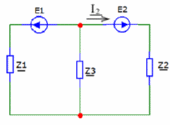



Рисунок 37 - Схема с направлением I3

Заменим ветвь, по которой протекает искомый ток короткозамкнутым отрезком. Направление тока короткого замыкания I_k выбираем совпадающим с направлением тока I. Искомая схема представлена на рисунке 38: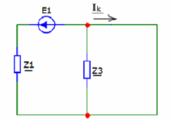



Рисунок 38 - Схема с короткозамкнутым отрезком

Вычисляем ток I_k методом наложения:



Cоставим схему 3 для вычисления Z_эк. Для этого источники ЭДС заменяем короткозамкнутыми отрезками. Исходная схема представлена на рисунке 39: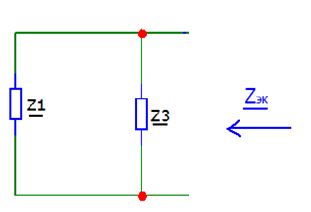



Рисунок 36 - Исходная схема



Составим схему эквивалентного генератора тока: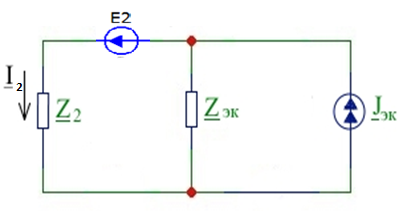



Рисунок 40 - Схема эквивалентного генератора тока

Из схемы:



Ответ:

4. Баланс комплексных мощностей

Исходная электрическая цепь представлена на рисунке 41: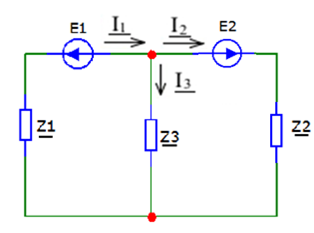



Рисунок 37 - Исходная цепь

Рассчитанные комплексные токи: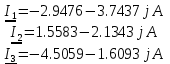



Задаем значения комплексно-сопряженных токов: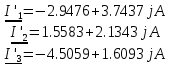



Мощность источников:



Мощность приёмников:



Относительная погрешность баланса мощностей по действительной части: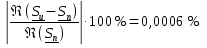

Таким образом, баланс сошёлся с точностью .

Относительная погрешность баланса мощностей по мнимой части: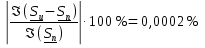



Таким образом, баланс сошёлся с точностью .

Диаграммы мощностей действительной и мнимой части представлены соответственно на рисунках 42 и 43.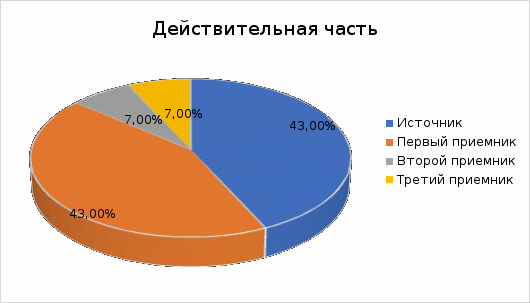



Рисунок 38 - Диаграмма мощности действительной части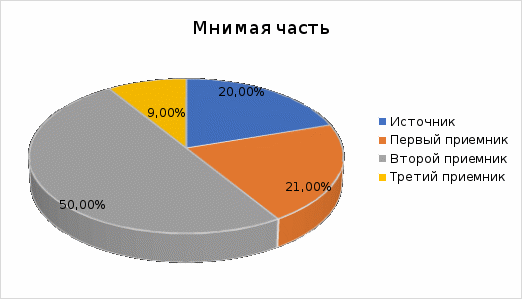



Рисунок 39 - Диаграмма мощности мнимой части

4. Заключение

В курсовой работе были применены методы для расчета комплексных токов такие как: метод уравнений Кирхгофа для комплексных величин, метод контурных токов для комплексных величин, узловых потенциалов для комплексных величин, метод двух узлов для комплексных величин, метод наложения для комплексных величин, метод эквивалентного генератора ЭДС для комплексных величин, метод эквивалентного генератора тока для комплексных величин.

Методами уравнения Кирхгофа, контурных токов, узловых потенциалов, двух узлов и наложения для комплексных величин были найдены все три комплексных тока в цепи.

Метод эквивалентного генератора ЭДС для комплексных величин был найден ток I₁.

Метод эквивалентного источника тока для комплексных величин был найден ток I₂.

В каждом методе значения комплексных токов совпали.

Баланс активной мощности сошелся с точностью 0,0006%, а баланс реактивной мощности с точностью 0,0002%.

Список использованных источников

• 
  ГОСТ 7.32-2001. Отчет о научно-исследовательской работе.
  
• 
  http://frisk.ucoz.com/
  
• 
  http://model.exponenta.ru
  
• 
  electricalschool.info
  
• 
  https://www.scilab.org/
  
• 
  https://svetotehnika.pro/tools/toecalc/
  
• 
  Фриск В.В. Основы теории цепей. Учебное пособие. –М.: ИП РадиоСофт, 2002.
  
• 
  Фриск В.В. Основы теории цепей. Сборник задач с примерами применения персонального компьютера. –М.:СОЛОН-Пресс, 2003.
  
• 
  Смирнов Н.И., Фриск В.В. Теория электрических цепей: конспект лекций. Учебное пособие для вузов.–М.:Горячая линия – Телеком, 2016.
  
• 
  Фриск В.В. Основы теории цепей. Расчёты и моделирование с помощью пакета компьютерной математики Mathcad. – М.:СОЛОН-Пресс, 2006.
  
• 
  Шебес М.Р., Каблукова М.В. Задачник по теории линейных электрических цепей. – М.: Высшая школа, 1990.
  
• 
  Колесников В.В. Основы теории цепей. – СПб., 2006.
  
• 
  Бакалов В.П., Дмитриков В.Ф., Крук Б.И. Основы теории цепей. –М.: Радио и связь, 2003.
  
• 
  Добротворский И.Н. Теория электрических цепей. – М: Радио и связь, 1989.
  
• 
  Зевеке Г.В., Ионкин П.А., Нетушил А.В.,Страхов. С.В. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. – М.:Энергия, 1975.
  
• 
  Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. – М.: Гардарики, 2007.
  
• 
  Бакалов В.П., Дмитриков В.Ф., Крук Б.И. Основы теории цепей. –М.: Радио и связь, 2003