ТОЭ Курсовая 3 вариант. Тоэ Курсовая 3 вариант. Курсовая работа студент гр. Проверил Елисеев С. Н. Москва 2021 г. Оглавление Задание 1 3 Введение 3

• Название: Курсовая работа студент гр. Проверил Елисеев С. Н. Москва 2021 г. Оглавление Задание 1 3 Введение 3
• Анкор: ТОЭ Курсовая 3 вариант
• Дата: 11.11.2021
• Размер: 1.17 Mb.
• Имя файла: Тоэ Курсовая 3 вариант.docx
• Тип: Курсовая; #269270
• страница: 6 из 8

Обозначения и сокращения

f – частота Гц;

L – индуктивность Гн;

C – емкость Ф;

ω – угловая частота ;

I – комплексный ток А;

E – комплексное напряжение В;

Z – комплексное сопротивление Ом;

S_и – комплексная мощность источника ВА;

S_пр – комплексная мощность приемника ВА;

R – сопротивление, Ом;

V – потенциал, В;

U – напряжение, В;

Ny – число узлов;

Nв – число ветвей;

Nт– число источников тока;

Nи – число ветвей, соединяющих только идеальные источники ЭДС;

- сумма проводимостей ветвей, присоединенных к первому узлу;

- алгебраическая сумма произведений ЭДС ветвей, примыкающих к 1-ому узлу, на их проводимость;

– напряжение холостого хода, В.

2. Расчёт разветвлённых цепей синусоидального тока

Объектом исследования данной работы являлась электрическая схема, представленная на рисунке 23: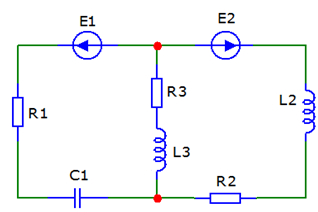



Рисунок 23 - Исходная схема

Исходные данные:

N = 3;

;

;

;

;

;



;

;

;

ω = 2·π·f;

ω = 314,1593

Преобразованная схема показана на рисунке 24.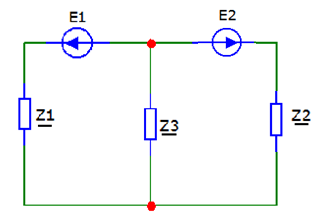



Рисунок 24 - Преобразованная схема

= 4 – 15,6882j Ом

= 5 + 2,8260j Ом

= 8 + 4,0820j Ом

2.1. Метод уравнений Кирхгофа

Для использования данного метода необходимо произвольно задать направление токов во всех ветвях цепи, что продемонстрировано на рисунке 25: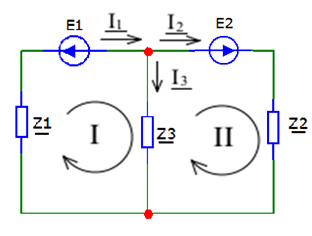



Рисунок 25 - Схема с направлениями токов

Рассчитываем необходимое количество уравнений по первому и второму законам Кирхгофа:



- количество ветвей;

- количество узлов.

Уравнение по 1-ому Закону Кирхгофа:



Для записи уравнений по 2-ому закону Кирхгофа произвольно выбирается первый контур и в нём произвольно задаётся положительное направление обхода контура. Затем из цепи мысленно удаляется какая-либо ветвь (для обеспечения независимости уравнений во 2-ом законе Кирхгофа друг от друга) и снова задаётся положительное направление обхода контура для оставшегося участка.

Для каждого контура записываются уравнения по 2-ому закону Кирхгофа:

(I)

(II)

В итоге составляем систему уравнений и решаем ее: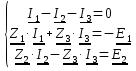



Данная система в эквивалентной матричной форме: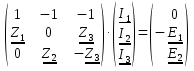



Значения токов вычисляются решением матричного уравнения:

Z*I=E

I=Z^-1*E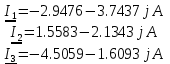



Ответ: ; ; .