готовая курсовая 2. Курсоваяработ а по дисциплине Математический анализ Поверхностные интегралы и их приложения Выполнил(а) студент (ка)
 Скачать 0.52 Mb. Скачать 0.52 Mb.
|
1.2 Физические приложения поверхностных интегралов первого типа1. С помощью поверхностных интегралов можно определять массы, моменты, координаты центров тяжести и т.п. величины для материальных поверхностей, вдоль которых распределены массы с определенной в каждой точке поверхностной плотностью. Масса оболочки Пусть S представляет собой тонкую гладкую оболочку. Распределение массы оболочки описывается функцией плотности 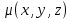 . Тогда полная масса оболочки выражается через поверхностный интеграл первого рода по формуле: . Тогда полная масса оболочки выражается через поверхностный интеграл первого рода по формуле: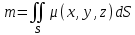 Центр масс и моменты инерции оболочки Пусть распределение массы m в тонкой оболочке описывается непрерывной функцией плотности 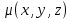 . Координаты центра масс оболочки определяются формулами . Координаты центра масс оболочки определяются формулами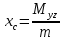 , ,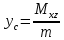 , ,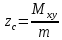 , где , где 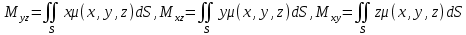 так называемые моменты первого порядка относительно координатных плоскостей x=0, y=0 и z=0, соответственно. Моменты инерции оболочки относительно осей 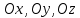 выражаются, соответственно, формулами: выражаются, соответственно, формулами:. 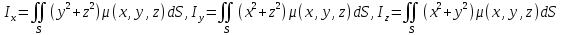 Моменты инерции оболочки относительно плоскостей 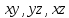 определяются формулами определяются формулами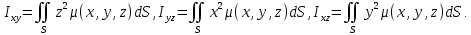   Рисунок3 Рисунок 4 П 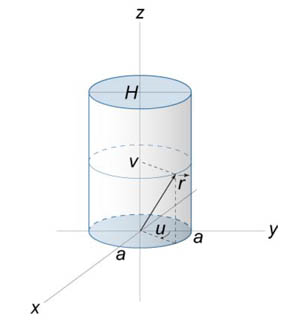 усть задана поверхность S, а в точке 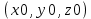 , не принадлежащей поверхности, находится тело массой m (рисунок 3,4) , не принадлежащей поверхности, находится тело массой m (рисунок 3,4) 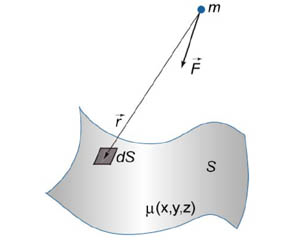 Сила притяжения между поверхностью S и точечным телом m определяется выражением Сила притяжения между поверхностью S и точечным телом m определяется выражением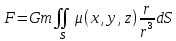 , ,где 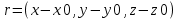 , G −гравитационная постоянная, , G −гравитационная постоянная, 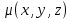 − функция плотности. − функция плотности.Сила давления Предположим, что поверхность S задана вектором r и находится под воздействием некоторой силы давления (это может быть плотина, крыло самолета, стенка баллона со сжатым газом и т.д.). Полная сила F, созданная давлением 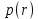 , находится с помощью поверхностного интеграла по формуле: , находится с помощью поверхностного интеграла по формуле: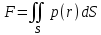 Давление, по определению, действует в направлении вектора нормали к поверхности S в каждой точке. Поэтому, мы можем записать 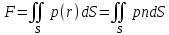 , где n − единичный нормальный вектор к поверхности S. , где n − единичный нормальный вектор к поверхности S.Поток жидкости и поток вещества Если в качестве векторного поля рассматривается скорость жидкости 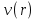 , то поток через поверхность S называется потоком жидкости. Он равен объему жидкости, проходящей через поверхность S в единицу времени и выражается формулой , то поток через поверхность S называется потоком жидкости. Он равен объему жидкости, проходящей через поверхность S в единицу времени и выражается формулой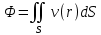 Аналогично, поток векторного поля 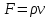 , где ρ − плотность, называется потоком вещества и определяется выражением , где ρ − плотность, называется потоком вещества и определяется выражением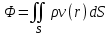 Он численно равен массе вещества, проходящего через поверхность S в единицу времени. (Основано на Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. Т.2. Санкт – Петербург: Лань, 1997 – 337 – 339с) 2. Притяжение простого слоя. Поверхностные интегралы первого типа естественно входят в рассмотрение при изучении притяжения масс, распределенных на поверхности. Пусть по поверхности (S) непрерывным образом распределены массы с заданной в каждой точке M (x, y, z) поверхности плотностью 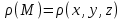 Пусть, далее, в точке 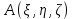 находится единица массы. Требуется определить, с какой по величине и по направлению силой находится единица массы. Требуется определить, с какой по величине и по направлению силой 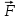 притягивается точка А поверхностью (S), если в основу положен ньютонов закон притяжения (закон всемирного тяготения). притягивается точка А поверхностью (S), если в основу положен ньютонов закон притяжения (закон всемирного тяготения).Если бы точка А притягивалась одной лишь материальной точкой М (x, y, z) с сосредоточенной в ней массой m, то величина силы притяжения была бы равна 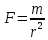 где r есть расстояние 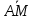 , т.е. , т.е.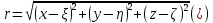 Так как эта сила направлена от А к М, то ее направляющие косинусы будут 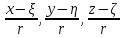 В случае системы притягивающих материальных точек эти выражения заменились бы суммами подобных выражений; наконец, при непрерывном распределении масс по поверхности появится вместо суммы интегралы. Применяя обычный прием изложения, можно было бы рассмотреть элемент dS поверхности с массой 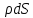 , как бы сосредоточенной в одной из его точек М (x, y, z). Оказываемое им на точку А притяжение будет иметь проекции на оси: , как бы сосредоточенной в одной из его точек М (x, y, z). Оказываемое им на точку А притяжение будет иметь проекции на оси: 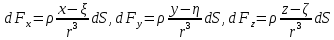 где r означает расстояние 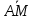 , выражаемое формулой (*). Теперь остается лишь просуммировать эти выражения, что приведет к следующим формулам для проекции силы , выражаемое формулой (*). Теперь остается лишь просуммировать эти выражения, что приведет к следующим формулам для проекции силы 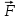 притяжения простого слоя на оси : притяжения простого слоя на оси :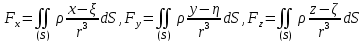 Этим сила 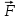 определена полностью как по величине, так и по направлению. определена полностью как по величине, так и по направлению.Если бы притягиваемая точка А и сама лежала на поверхности (S), то проекции притяжения на оси по-прежнему выражались бы этими интегралами, но на этот раз интегралы эти были бы несобственными, поскольку вблизи точки А подынтегральные функции все перестают быть ограниченными. 3.Потенциал простого поля (Основано на Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. Т.2. Санкт – Петербург: Лань, 1997 – 316 – 319с) |
