готовая курсовая 2. Курсоваяработ а по дисциплине Математический анализ Поверхностные интегралы и их приложения Выполнил(а) студент (ка)
 Скачать 0.52 Mb. Скачать 0.52 Mb.
|
1.3.1 Выражение поверхностного интеграла II-го рода через двойной интеграл.Пусть поверхность Ω задается уравнением  , где функция , где функция 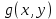 удовлетворяет условиям, сформулированным в примере 2 п.1.2, т.е. определена на ограниченной области D плоскости OXY, непрерывна на ней и имеет непрерывные частные производные первого порядка. Зададим, как и выше, разбиение T поверхности Ω, а проекции частей Ωk на плоскость OXY обозначим через Dk. Запишем интегральную сумму для поверхностного интеграла II-го рода от функции f(M), заданной на поверхности. Для верхней стороны поверхности интегральная сумма имеет вид: удовлетворяет условиям, сформулированным в примере 2 п.1.2, т.е. определена на ограниченной области D плоскости OXY, непрерывна на ней и имеет непрерывные частные производные первого порядка. Зададим, как и выше, разбиение T поверхности Ω, а проекции частей Ωk на плоскость OXY обозначим через Dk. Запишем интегральную сумму для поверхностного интеграла II-го рода от функции f(M), заданной на поверхности. Для верхней стороны поверхности интегральная сумма имеет вид: Учитывая, что точка Mk лежит на поверхности, т.е. 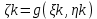 , равенство (8) можно переписать в виде: , равенство (8) можно переписать в виде: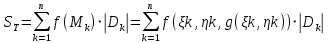 что представляет собой интегральную сумму для двойного интеграла: 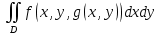 Переходя к пределу при Переходя к пределу при  , получаем: , получаем: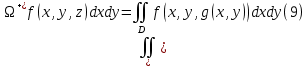 Для нижней стороны поверхности в силу формулы (2') получаем: 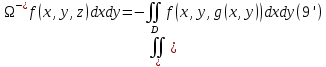 Аналогичные формулы могут быть записаны и для интегралов 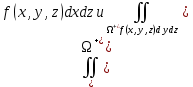 1.4 Формула Стокса.Формула Стокса обобщает формулу Грина на случай пространственной кривой. Она устанавливает связь между поверхностным интегралом по поверхности Ω и криволинейным интегралом II-го рода по ее границе. Пусть поверхность Ω, задана параметрически на ограниченной области ∆ в плоскости переменных (u, v) соотношениями (3) из п.1.2: 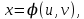 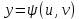 , , 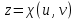 , ,причем для этих функций справедливы условия гладкости Выберем определенную сторону поверхности Ω, например, сторону 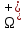 , на которой положительное направление обхода границы Г(Ω) поверхности Ω отвечает на плоскости переменных , на которой положительное направление обхода границы Г(Ω) поверхности Ω отвечает на плоскости переменных 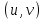 положительному обходу границы Г(∆) области ∆ (т.е. при движении точки по границе поверхности Ω в положительном направлении, ее проекция на границу области ∆ движется против часовой стрелки).Границы областей с выбранными на них положительными направлениями обхода будем обозначать через положительному обходу границы Г(∆) области ∆ (т.е. при движении точки по границе поверхности Ω в положительном направлении, ее проекция на границу области ∆ движется против часовой стрелки).Границы областей с выбранными на них положительными направлениями обхода будем обозначать через 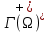 и и 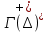 . .Пусть на поверхности Ω (вместе с некоторой ее окрестностью) функция 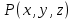 определена, непрерывна и имеет непрерывные частные производные. определена, непрерывна и имеет непрерывные частные производные. Рассмотрим криволинейный интеграл II-го рода от этой функции по кривой 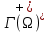 . Используя соотношения (3) п.1.2. и формулу для дифференциала сложной функции, получим: . Используя соотношения (3) п.1.2. и формулу для дифференциала сложной функции, получим: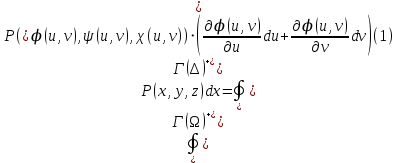 Кривая 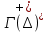 и ограниченная ею область ∆ лежат в плоскости и ограниченная ею область ∆ лежат в плоскости 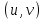 , поэтому к интегралам (1) можно применить формулу Грина: , поэтому к интегралам (1) можно применить формулу Грина: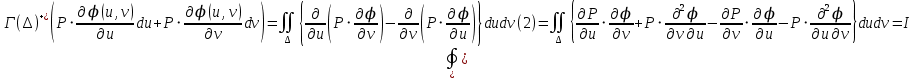 При условиях, наложенных на функции 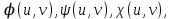 справедливо равенство: справедливо равенство: 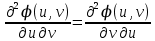 .Тогда из (2) получаем .Тогда из (2) получаем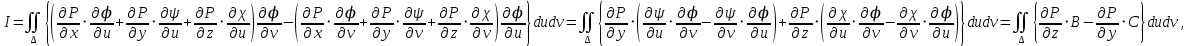 где 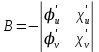 , , 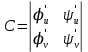 Теперь по формулам (10) и (7) из п.1.3. окончательно получаем 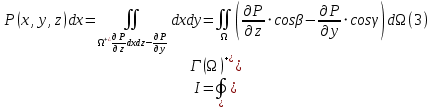 Аналогично можно получить равенства: 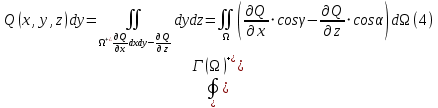 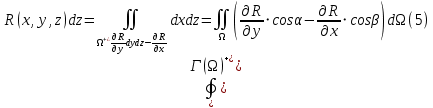 ( В равенствах (3) – (5) величины cosα, cosβ, cosγ есть направляющие косинусы вектора нормали к поверхности 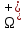 ). ). Складывая соотношения (3) – (5) получаем формулу Стокса: 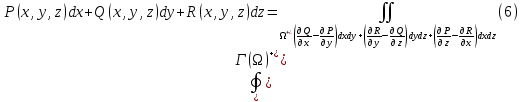 Формулу Стокса можно записать и через поверхностный интеграл I-го рода: 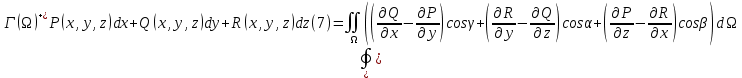 Замечание 1. Вектор 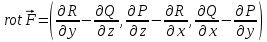 называется ротором, или вихрем векторной функции называется ротором, или вихрем векторной функции 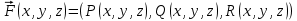 .Компоненты ротора удобно выразить с помощью определителя: .Компоненты ротора удобно выразить с помощью определителя: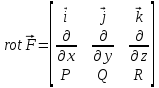 С использованием понятия ротора формула Стокса записывается короче: 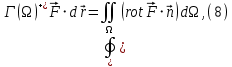 и выражает циркуляцию вектора через поверхностный интеграл от его ротора. (Основано на Калинин В.В., Петрова И.В. К 18 Математика в нефтегазовом образовании. Теория и задачи: Учеб. пособие. − М.: РГУ нефти и газа им. И.М. Губкина, 2005. Вып. 3. Часть 2: Кратные, криволинейные и поверхностные интегралы – 161- 165с) |
