Дмиок курсовой редуктор. пз. Курсовой проект по Детали машин и основы конструирования наименование дисциплины
 Скачать 0.73 Mb. Скачать 0.73 Mb.
|
3 РАСЧЕТ БЫСТРОХОДНОЙ ЦИЛИНДРИЧЕСКОЙ КОСОЗУБОЙ ПЕРЕДАЧИ РЕДУКТОРА3.1 Цель Провести проектный и проверочный расчеты цилиндрической зубчатой косозубой быстроходной передачи редуктора. 3.2 Расчетная схема 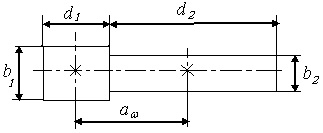 Рисунок 2.1 – Геометрические параметры цилиндрической зубчатой передачи 3.3 Данные для расчета Данные для расчета передачи берем из кинематического расчета. Для шестерни берем значения с первого вала, а для колеса со второго вала. Таблица 2.1 Силовые и скоростные параметры для расчета промежуточной передачи
3.4 Условие расчета Проектный расчет ведем по условию прочности на контакт, так как основной вид разрушения закрытых зубчатых передач - это поверхностное выкашивание зубьев в зоне контакта. Проверочный расчет проводим и на контакт и на изгиб. 3.5 Выбор материала и расчет допускаемых напряжений Материал и расчет допускаемых напряжений быстроходной цилиндрической прямозубой передачи совпадает с материалом и расчетом допускаемых напряжений тихоходной цилиндрической косозубой передачи и описан в пункте 2.5 3.6 Проектный расчет передачи Определяем межосевое расстояние по формуле 2.9: 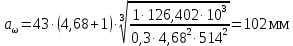 Коэффициент ширины венца колеса, принимаем ba=0,3 (с 20 [1]). Полученное значение межосевого расстояния aω округляют в большую сторону до стандартного по СТ СЭВ 310-76: 40, 50, 63, 71, 80, 90, 100, 112, 125, 140, 160, 180, 200, 220, 250, 280, 315 мм. Принимаем межосевое расстояние равным, (табл.19.1 [1]): 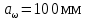 Определяем модуль зацепления. Выбирают модуль по формуле 2.10 в интервале: 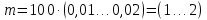 Модуль принимаем из стандартного ряда равным: 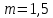 Определяем суммарное число зубьев по формуле 2.11: 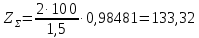 Принимаем суммарное число зубьев равным: 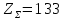 Определяем число зубьев шестерни по формуле 2.12: 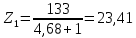 Принимаем число зубьев шестерни равным: 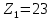 Определяем число зубьев колеса по формуле 2.13: 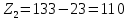 Уточняем фактическое передаточное отношение по формуле 2.14: 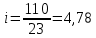 Уточняем угол наклона зуба по формуле 2.15: 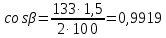 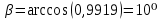 Определяем размеры зубчатых колес. Делительный диаметр шестерни рассчитываем по формуле 2.16: 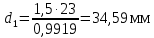 Делительные диаметры колеса по формуле 2.17: 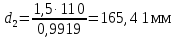 Диаметры окружности впадин зубьев шестерни по формуле 2.18: 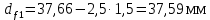 Диаметры окружности впадин зубьев колеса по формуле 2.19: 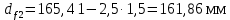 Диаметры окружности вершин зубьев шестерни по формуле 2.20: 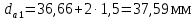 Диаметры окружности вершин зубьев колеса по формуле 2.21: 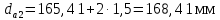 Определяем ширину шестерни и колеса. Ширину колеса находим по формуле 2.22: 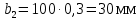 Принимаем ширину колеса равную: 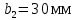 Определяем ширину шестерни по формуле 2.23: 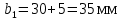 Принимаем ширину шестерни равную: 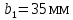 3.7 Проверка зубьев колес по напряжениям изгиба Определяем силы в зацеплении. Окружная сила направлена по касательной в точки касания колеса и шестерни и определяется по формуле 2.24: 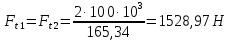 Радиальная сила направлена к центру окружности и определяется по формуле 2.25: 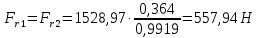 Осевая сила направлена вдоль оси и находится по формуле 2.26: 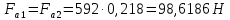 Проверяем зубья колес по напряжениям изгиба. Должны выполняться неравенства 2.27 и 2.28. Определяем напряжение на изгиб зуба колеса по формуле 2.29: 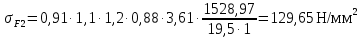 Значения коэффициентов KFα,KFv,KFβ,Yβ, YFS совпадает со значениями коэффициентов KFα,KFv,KFβ,Yβ, YFS в пункте 2.9. Так как [σ]F2=256 Н/мм2 и σF2= 124,61 Н/мм2, что удовлетворяет условию 2.27 , то колесо прошло проверку по напряжениям на изгиб. 3.8 Проверка зубьев колес по напряжениям на контакт Проверяем зубья колес по напряжениям контакта. Расчётное контактное напряжение вычисляется по формуле 2.30: 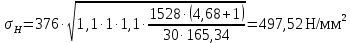 Значения коэффициентов KH, KH, KHV совпадает со значениями коэффициентов KH, KH, KHV в пункте 2.8. Допускаем 10% перегруза и 5% недогруза, то есть должно выполнятся условие формулы 2.30. 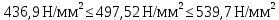 Так как [σ]H= 497,52 Н/мм2, что находится в допустимых пределах, то колеса прошли проверку по напряжениям на изгиб. |

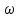 , с-1
, с-1