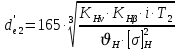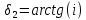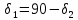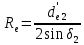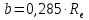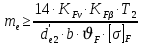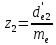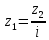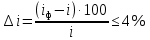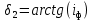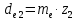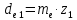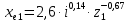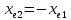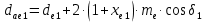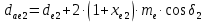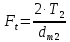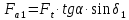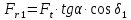Дмиок курсовой редуктор. пз. Курсовой проект по Детали машин и основы конструирования наименование дисциплины

• Название: Курсовой проект по Детали машин и основы конструирования наименование дисциплины
• Анкор: Дмиок курсовой редуктор
• Дата: 13.05.2023
• Размер: 0.73 Mb.
• Имя файла: пз.docx
• Тип: Курсовой проект; #1126245
• страница: 4 из 12

4 РАСЧЕТ ОТКРЫТОЙ КОНИЧЕСКОЙ ПЕРЕДАЧИ

4.1 Цель

Провести проектный и проверочный расчеты открытой конической передачи.

4.2 Расчетная схема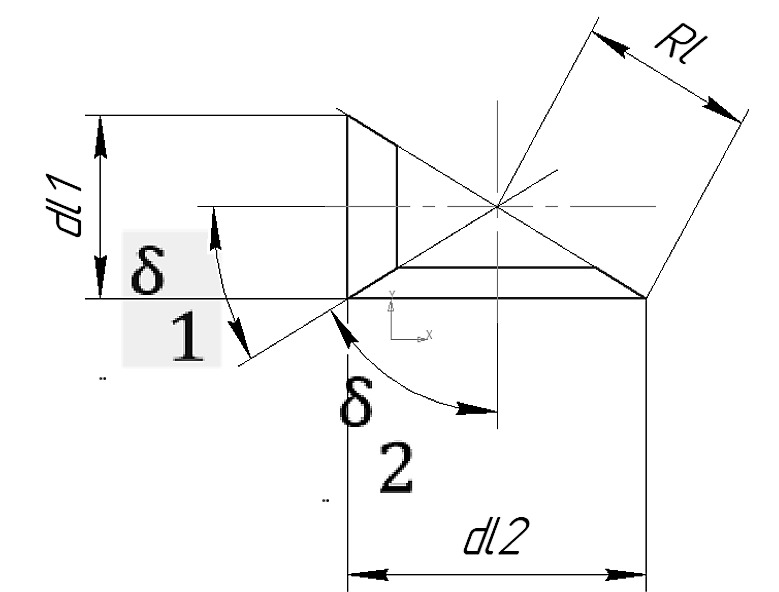

Рисунок 4.1 – Схема конической передачи

4.3 Данные для расчета

Данные для расчета передачи берем из кинематического расчета.

P₁ = P_III = 7,891 кВт;

P₂ = P_IV = 7,5 кВт;

n₁ = n_III = 171,79 об/мин;

n₂ = n_IV = 53,68 об/мин;

ω₁ = ω_III = 17,98 с^-1;

ω₂ = ω_IV = 5,61 с^-1;

T₁ = T_III = 438,85 Н·м;

T₂ = T_IV = 1334,75 Н·м;

i_кп = 3,2.

4.4 Условие расчета

Проектный расчет открытой конической передачи ведем так же на контакт, но для компенсации повышенного износа модуль выбираем побольше и проверяем зубья на изгиб.

4.5 Выбор материала и расчет допускаемых напряжений

Материал и расчет допускаемых напряжений открытой конической передачи совпадает с материалом и расчетом допускаемых напряжений тихоходной цилиндрической прямозубой передачи и описан в пункте 2.5.

4.6 Проектный расчёт

Диаметр внешней делительной окружности колеса определяется по формуле (с 28 [1]):

(4.1)

где K_Hv - Коэффициент, учитывающий внутреннюю динамику нагружения. Для прямозубых при твердости зубьев ≤ 350 HB K_Hv = 1,25 (с 27[1]);

K_H - коэффициент неравномерности распределения нагрузки по длине зуба. Для круговых зубьев K_H= 1 (с 27[1]);

i - передаточное отношение передачи;

Т₂ - вращающий момент на валу колеса (по заданию значение берем с 4 вала), Н·м;

_H – коэффициент, _H= 0,85; (с 27[1]);

[]_H - допускаемое контактное напряжение колеса с менее прочным зубом или среднее допускаемое контактное напряжение, []_H= 514 Н/мм².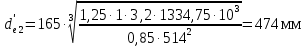

Определяем углы делительных конусов колеса по формуле (с 28 [1]):

(4.2)

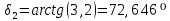Определяем углы делительных конусов шестерни по формуле (с 28 [1]):

(4.3)

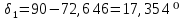Определяем конусное расстояние по формуле (с 28 [1]):

(4.4)

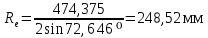Определяем ширину колёс (с 28 [1]):

(4.5)

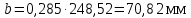Принимаем ширину колёс :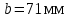

Определяем модуль передачи.

Внешний окружной модуль передачи:

(4.6)

где 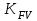- коэффициент динамической нагрузки, зависящий от ок­ружной скорости колес и степени точности передачи , 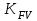=1,5 (с 28 [1]);

K_Fβ- коэффициент неравномерности нагрузки по длине зуба, для прямозубых колёсK_Fβ =1 (с 28 [1]);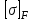

- допускаемое изгибное напряжение колеса с менее прочным зубом или среднее допускаемое изгибное напряжение, 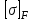= 256 Н/мм²;

_F - коэффициент, для прямозубых колёс равный _F= 0,85; (с 28 [1]).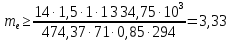

Принимаем модуль равный: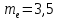
мм
Определяем число зубьев колеса по формуле (с 29 [1]):

(4.7)

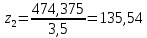Принимаем число зубьев колеса равное: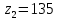

Определяем число зубьев шестерни по формуле (с 29 [1]):

(4.8)

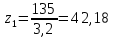Принимаем число зубьев шестерни равное: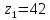

Уточняем фактическое передаточное отношение по формуле 2.14: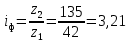

Отклонение от заданного передаточного числа не должно превышать 4%:

(4.9)

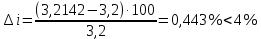Отклонения фактического передаточного числа от заданного в пределах нормы.

Определяем окончательные значения размеров колес.

Уточняем углы делительных конусов колеса по формуле (с 29 [1]):

(4.10)

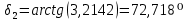Уточняем углы делительных конусов шестерни по формуле (с 29 [1]):

(4.11)

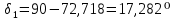Делительные диаметры колеса и шестерни (с 29 [1]):

(4.12)

(4.13)

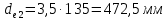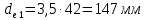Коэффициенты x_e1 и x_e2 смещения для шестерни и колеса (с 30 [1]):

(4.14)

(4.15)

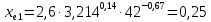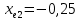Внешние диаметры колёс (c 30 [1]):

(4.16)

(4.17)

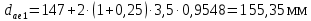
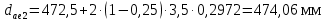Силы зацепления.

Окружная сила на среднем диаметре колеса (c 31 [1]):

(4.20)

где d_m2 = 0,857d_e2 = 404,93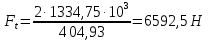

Осевая сила на шестерне (c 31 [1]):

(4.21)

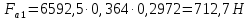Радиальная сила на шестерне (c 31 [1]):

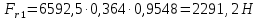(4.22)