Курсовая информатика. Курсовой проект по дисциплине Архитектура и организация эвм Тема Использование табличного редактора для выполнения операций с числами в различных системах счисления. Обзор языков программирования баз данных.

• Название: Курсовой проект по дисциплине Архитектура и организация эвм Тема Использование табличного редактора для выполнения операций с числами в различных системах счисления. Обзор языков программирования баз данных.
• Анкор: Курсовая информатика
• Дата: 01.06.2022
• Размер: 5.94 Mb.
• Имя файла: informatika.rtf
• Тип: Курсовой проект; #563583

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

(ФГБОУ ВО «ВГТУ», ВГТУ)

Факультет информационных технологий и компьютерной безопасности

(факультет)

Кафедра графики, конструирования и информационных технологий в промышленном дизайне
КУРСОВОЙ ПРОЕКТ
по дисциплине: «Архитектура и организация ЭВМ»

Тема: «Использование табличного редактора для выполнения операций с числами в различных системах счисления. Обзор языков программирования баз данных.»
	Расчетно-пояснительная записка
Разработал студент			Д.А. Босых

Подпись, дата Инициалы, фамилия
Руководитель А.В. Норман

Подпись, дата Инициалы, фамилия
Члены комиссии

Подпись, дата Инициалы, фамилия

Подпись, дата Инициалы, фамилия

Подпись, дата Инициалы, фамилия

Нормоконтролер

Подпись, дата Инициалы, фамилия

Защищена __________________ Оценка ____________________________

дата
ВОРОНЕЖ

2021

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

(ФГБОУ ВО «ВГТУ», ВГТУ)

Факультет информационных технологий и компьютерной безопасности

(Факультет)

Кафедра систем информационной безопасности
ЗАДАНИЕ

на курсовой проект

по дисциплине: «Информатика»
Тема: «Использование табличного редактора для выполнения операций с числами в различных системах счисления. Обзор языков программирования баз данных.»

Студент
		Группа, фамилия, имя, отчество
Номер варианта
Технические условия		процессор AMD Ryzen 3800 CPU 3.90 ГГц,

операционная система Windows 10 Pro, ОЗУ 16384 МБ
Содержание и объем работы (графические работы, расчеты и прочее):

Сроки выполнения этапов:

Срок защиты курсового проекта: г.
Руководитель

Подпись, дата Инициалы, фамилия
Задание принял студент

Подпись, дата Инициалы, фамилия

1. Системы счисления с различными основаниями и правила использования арифметических операций в них 7

1.1. Позиционные системы счисления с различным основанием 8

1.1.1. Перевод из одной системы счисления в другую 12

1.2. Изучение правил перевода чисел в различные системы счисления 14

1.3 Образование десятичной системы счисления 16

2. Разработка программы 18

2.1 Структура программы 20

2.2 Код программы и примеры выполнения 21

Список литературы 24

Введение
На ранних ступенях развития общества люди почти не умели считать. Они отличали друг от друга совокупности двух и трех предметов; всякая совокупность, содержавшая большее число предметов, объединялась в понятии «много». Это был еще не счет, а лишь его зародыш.

Впоследствии способность различать друг от друга небольшие совокупности развивалась; возникли слова для обозначений понятий «четыре», «пять», «шесть», «семь». Последнее слово длительное время обозначало также неопределенно большое количество.

С усложнением хозяйственной деятельности людей понадобилось вести счет в более обширных пределах. Для этого человек пользовался окружавшими его предметами, как инструментами счета: он делал зарубки на палках и на деревьях, завязывал узлы на веревках, складывал камешки в кучки и т.п. Это удобно, так как сразу визуально определяется количество знаков и сопоставляется с количеством предметов, которые эти знаки обозначают. Все мы ходили в первый класс и считали там на счетных палочках – это отзвук той далекой эпохи. Кстати, от счета с помощью камешков ведут свое начало различные усовершенствованные инструменты, как, например, русские счеты, китайские счеты («сван-пан»), древнеегипетский «абак» (доска, разделенная на полосы, куда клались жетоны). Аналогичные инструменты существовали у многих народов. Более того, в латинском языке понятие «счет» выражается словом «calculatio» (отсюда наше слово «калькуляция»); а происходит оно от слова «calculus», означающего «камешек».

Особо важную роль играл природный инструмент человека – его пальцы. Этот инструмент не мог длительно хранить результат счета, но зато всегда был «под рукой» и отличался большой подвижностью. Язык первобытного человека был беден; жесты возмещали недостаток слов, и числа, для которых еще не было названий, «показывались» на пальцах.

Поэтому, вполне естественно, что вновь возникавшие названия «больших» чисел часто строились на основе числа 10 – по количеству пальцев на руках; у некоторых народов возникали также названия чисел на основе числа 5 – по количеству пальцев на одной руке или на основе числа 20 – по количеству пальцев на руках и ногах.

На первых порах расширение запаса чисел происходило медленно. Сначала люди овладели счетом в пределах нескольких десятков и лишь позднее дошли до сотни. У многих народов число 40 долгое время было пределом счета и названием неопределенно большого количества. В русском языке слово «сороконожка» имеет смысл «многоножка»; выражение «сорок сороков» означало в старину число, превосходящее всякое воображение.

На следующей ступени счет достигает нового предела: десяти десятков, и создается название для числа 100. Вместе с тем слово «сто» приобретает смысл неопределенно большого числа. Такой же смысл приобретают потом последовательно числа тысяча, десять тысяч (в старину это число называлось «тьма»), миллион.

На современном этапе границы счета определены термином «бесконечность», который не обозначает, какое-либо конкретное число.

Обозначение чисел в разных системах счисления

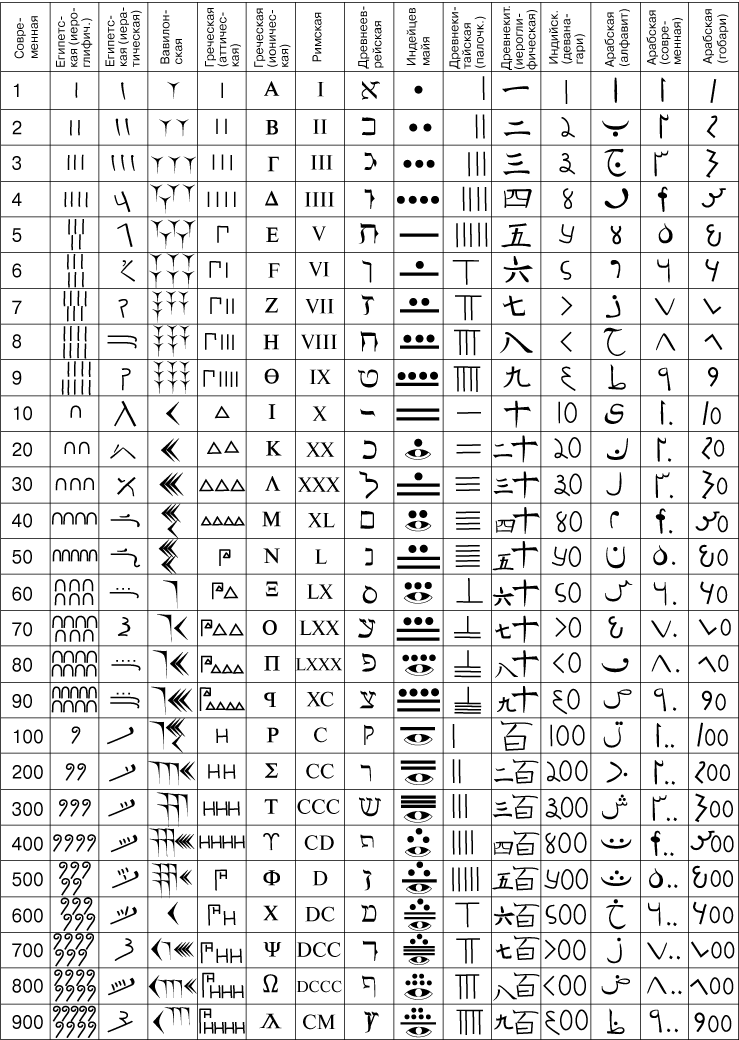1. Системы счисления с различными основаниями и правила использования арифметических операций в них
Система счисления — это способ записи (представления) чисел.

Что под этим подразумевается? Например, вы видите перед собой несколько деревьев. Ваша задача — их посчитать. Для этого можно — загибать пальцы, делать зарубки на камне (одно дерево — один палец\зарубка) или сопоставить 10 деревьям какой-нибудь предмет, например, камень, а единичному экземпляру — палочку и выкладывать их на землю по мере подсчета. В первом случае число представляется, как строка из загнутых пальцев или зарубок, во втором — композиция камней и палочек, где слева — камни, а справа — палочки.

Системы счисления подразделяются на позиционные и непозиционные, а позиционные, в свою очередь, — на однородные и смешанные.

- Непозиционная — самая древняя, в ней каждая цифра числа имеет величину, не зависящую от её позиции (разряда). То есть, если у вас 5 черточек — то число тоже равно 5, поскольку каждой черточке, независимо от её места в строке, соответствует всего 1 один предмет.

- Позиционная система — значение каждой цифры зависит от её позиции (разряда) в числе. Например, привычная для нас 10-я система счисления — позиционная. Рассмотрим число 453. Цифра 4 обозначает количество сотен и соответствует числу 400, 5 — кол-во десяток и аналогично значению 50, а 3 — единиц и значению 3. Как видим — чем больше разряд — тем значение выше. Итоговое число можно представить, как сумму 400+50+3=453.

- Однородная система — для всех разрядов (позиций) числа набор допустимых символов (цифр) одинаков. В качестве примера возьмем упоминавшуюся ранее 10-ю систему. При записи числа в однородной 10-й системе вы можете использовать в каждом разряде исключительно одну цифру от 0 до 9, таким образом, допускается число 450 (1-й разряд — 0, 2-й — 5, 3-й — 4), а 4F5 — нет, поскольку символ F не входит в набор цифр от 0 до 9.

- Смешанная система — в каждом разряде (позиции) числа набор допустимых символов (цифр) может отличаться от наборов других разрядов. Яркий пример — система измерения времени. В разряде секунд и минут возможно 60 различных символов (от «00» до «59»), в разряде часов – 24 разных символа (от «00» до «23»), в разряде суток – 365 и т. д.
1.1. Позиционные системы счисления с различным основанием
Как упоминалось выше — первые предпосылки к появлению позиционной системы возникли в древнем Вавилоне. В Индии система приняла форму позиционной десятичной нумерации с применением нуля, а у индусов эту систему чисел заимствовали арабы, от которых её переняли европейцы. По каким-то причинам, в Европе за этой системой закрепилось название “арабская”.

Десятичная система счисления:

Это одна из самых распространенных систем счисления. Именно её мы используем, когда называем цену товара и произносим номер автобуса. В каждом разряде (позиции) может использоваться только одна цифра из диапазона от 0 до 9. Основанием системы является число 10.

Для примера возьмем число 503. Если бы это число было записано в непозиционной системе, то его значение равнялось 5+0+3 = 8. Но у нас — позиционная система и значит каждую цифру числа необходимо умножить на основание системы, в данном случае число “10”, возведенное в степень, равную номеру разряда. Получается, значение равно 5*10² + 0*10¹ + 3*10⁰ = 500+0+3 = 503. Чтобы избежать путаницы при одновременной работе с несколькими системами счисления основание указывается в качестве нижнего индекса. Таким образом, 503 = 503₁₀.

Помимо десятичной системы, отдельного внимания заслуживают 2-, 8-, 16-ая системы.

Двоичная система счисления:

Эта система, в основном, используется в вычислительной технике. Почему не стали использовать привычную нам 10-ю? Первую вычислительную машину создал Блез Паскаль, использовавший в ней десятичную систему, которая оказалась неудобной в современных электронных машинах, поскольку требовалось производство устройств, способных работать в 10 состояниях, что увеличивало их цену и итоговые размеры машины. Этих недостатков лишены элементы, работающие в 2-ой системе. Тем не менее, рассматриваемая система была создана за долго до изобретения вычислительных машин и уходит “корнями” в цивилизацию Инков, где использовались кипу — сложные верёвочные сплетения и узелки.

Двоичная позиционная система счисления имеет основание 2 и использует для записи числа 2 символа (цифры): 0 и 1. В каждом разряде допустима только одна цифра — либо 0, либо 1.

Примером может служить число 101. Оно аналогично числу 5 в десятичной системе счисления. Для того, чтобы перевести из 2-й в 10-ю необходимо умножить каждую цифру двоичного числа на основание “2”, возведенное в степень, равную разряду. Таким образом, число 101₂ = 1*2² + 0*2¹ + 1*2⁰ = 4+0+1 = 5₁₀.

Хорошо, для машин 2-я система счисления удобнее, но мы ведь часто видим, используем на компьютере числа в 10-й системе. Как же тогда машина определяет какую цифру вводит пользователь? Как переводит число из одной системы в другую, ведь в её распоряжении всего 2 символа — 0 и 1?

Чтобы компьютер мог работать с двоичными числами (кодами), необходимо чтобы они где-то хранились. Для хранения каждой отдельной цифры применяется триггер, представляющий собой электронную схему. Он может находится в 2-х состояниях, одно из которых соответствует нулю, другое — единице.

Для запоминания отдельного числа используется регистр — группа триггеров, число которых соответствует количеству разрядов в двоичном числе.

А совокупность регистров — это оперативная память. Число, содержащееся в регистре — машинное слово. Арифметические и логические операции со словами осуществляет арифметико-логическое устройство (АЛУ). Для упрощения доступа к регистрам их нумеруют. Номер называется адресом регистра. Например, если необходимо сложить 2 числа — достаточно указать номера ячеек (регистров), в которых они находятся, а не сами числа. Адреса записываются в 8- и 16-ричной системах (о них будет рассказано ниже), поскольку переход от них к двоичной системе и обратно осуществляется достаточно просто.

Для перевода из 2-й в 8-ю число необходимо разбить на группы по 3 разряда справа налево, а для перехода к 16-ой — по 4. Если в крайней левой группе цифр не достает разрядов, то они заполняются слева нулями, которые называются ведущими. В качестве примера возьмем число 101100₂. В восьмеричной — это 101 100 = 54₈, а в шестнадцатеричной — 0010 1100 = 2С₁₆.

Отлично, но почему на экране мы видим десятичные числа и буквы? При нажатии на клавишу в компьютер передаётся определённая последовательность электрических импульсов, причём каждому символу соответствует своя последовательность электрических импульсов (нулей и единиц).

Программа драйвер клавиатуры и экрана обращается к кодовой таблице символов (например, Unicode, позволяющая закодировать 65536 символов), определяет какому символу соответствует полученный код и отображает его на экране. Таким образом, тексты и числа хранятся в памяти компьютера в двоичном коде, а программным способом преобразуются в изображения на экране.

Восьмеричная система счисления:

8-я система счисления, как и двоичная, часто применяется в цифровой технике. Имеет основание 8 и использует для записи числа цифры от 0 до 7.
Пример восьмеричного числа: 254. Для перевода в 10-ю систему необходимо каждый разряд исходного числа умножить на 8ⁿ, где n — это номер разряда. Получается, что 254₈ = 2*8² + 5*8¹ + 4*8⁰ = 128+40+4 = 172₁₀.

Шестнадцатеричная система счисления:

Шестнадцатеричная система широко используется в современных компьютерах, например при помощи неё указывается цвет: #FFFFFF — белый цвет. Рассматриваемая система имеет основание 16 и использует для записи числа: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B. C, D, E, F, где буквы равны 10, 11, 12, 13, 14, 15 соответственно.

В качестве примера возьмем число 4F5₁₆. Для перевода в восьмеричную систему — сначала преобразуем шестнадцатеричное число в двоичное, а затем, разбив на группы по 3 разряда, в восьмеричное. Чтобы преобразовать число в 2-е необходимо каждую цифру представить в виде 4-х разрядного двоичного числа. 4F5₁₆ = (100 1111 101)₂. Но в 1 и 3 группах не достает разряда, поэтому заполним каждый ведущими нулями: 0100 1111 0101. Теперь необходимо разделить полученное число на группы по 3 цифры справа налево: 0100 1111 0101 = 010 011 110 101. Переведем каждую двоичную группу в восьмеричную систему, умножив каждый разряд на 2ⁿ, где n — номер разряда: (0*2²+1*2¹+0*2⁰) (0*2²+1*2¹+1*2⁰) (1*2²+1*2¹+0*2⁰) (1*2²+0*2¹+1*2⁰) = 2365₈.

Помимо рассмотренных позиционных систем счисления, существуют и другие, например:

1. 
   Троичная
   
2. 
   Четверичная
   
3. 
   Двенадцатеричная
   

Позиционные системы подразделяются на однородные и смешанные.

Смешанные системы счисления:

К уже приведенному определению можно добавить теорему: “если P=Qⁿ (P,Q,n – целые положительные числа, при этом P и Q — основания), то запись любого числа в смешанной (P-Q)-ой системе счисления тождественно совпадает с записью этого же числа в системе счисления с основанием Q.”

Опираясь на теорему, можно сформулировать правила перевода из P-й в Q-ю системы и наоборот:

1. 
   Для перевода из Q-й в P-ю, необходимо число в Q-й системе, разбить на группы по n цифр, начиная с правой цифры, и каждую группу заменить одной цифрой в P-й системе.
   
2. 
   Для перевода из P-й в Q-ю, необходимо каждую цифру числа в P-й системе перевести в Q-ю и заполнить недостающие разряды ведущими нулями, за исключением левого, так, чтобы каждое число в системе с основанием Q состояло из n цифр.
   

Яркий пример — перевод из двоичной системы счисления в восьмеричную. Возьмем двоичное число 10011110₂, для перевода в восьмеричное — разобьем его справа налево на группы по 3 цифры: 010 011 110, теперь умножим каждый разряд на 2ⁿ, где n — номер разряда, 010 011 110 = (0*2²+1*2¹+0*2⁰) (0*2²+1*2¹+1*2⁰) (1*2²+1*2¹+0*2⁰) = 236₈. Получается, что 10011110₂ = 236₈. Для однозначности изображения двоично-восьмеричного числа его разбивают на тройки: 236₈ = (10 011 110)_2-8.
1.1.1. Перевод из одной системы счисления в другую

Иногда требуется преобразовать число из одной системы счисления в другую, поэтому рассмотрим способы перевода между различными системами.

Преобразование в десятичную систему счисления:

Имеется число a₁a₂a₃ в системе счисления с основанием b. Для перевода в 10-ю систему необходимо каждый разряд числа умножить на bⁿ, где n — номер разряда. Таким образом, (a₁a₂a₃)_b = (a₁*b² + a₂*b¹ + a₃*b⁰)₁₀.
Пример: 101₂ = 1*2² + 0*2¹ + 1*2⁰ = 4+0+1 = 5₁₀

Преобразование из десятичной системы счисления в другие:

Целая часть:

1. 
   Последовательно делим целую часть десятичного числа на основание системы, в которую переводим, пока десятичное число не станет равно нулю.
   
2. 
   Полученные при делении остатки являются цифрами искомого числа. Число в новой системе записывают, начиная с последнего остатка.\
   

Дробная часть:

1. 
   Дробную часть десятичного числа умножаем на основание системы, в которую требуется перевести. Отделяем целую часть. Продолжаем умножать дробную часть на основание новой системы, пока она не станет равной 0.
   
2. 
   Число в новой системе составляют целые части результатов умножения в порядке, соответствующем их получению.
   

Пример: переведем 15₁₀ в восьмеричную:15\8 = 1, остаток 7 1\8 = 0, остаток 1 Записав все остатки снизу вверх, получаем итоговое число 17. Следовательно, 15₁₀ = 17₈.

Преобразование из двоичной в восьмеричную и шестнадцатеричную системы:

Для перевода в восьмеричную — разбиваем двоичное число на группы по 3 цифры справа налево, а недостающие крайние разряды заполняем ведущими нулями. Далее преобразуем каждую группу, умножая последовательно разряды на 2ⁿ, где n — номер разряда.

В качестве примера возьмем число 1001₂: 1001₂ = 001 001 = (0*2² + 0*2¹ + 1*2⁰) (0*2² + 0*2¹ + 1*2⁰) = (0+0+1) (0+0+1) = 11₈

Для перевода в шестнадцатеричную — разбиваем двоичное число на группы по 4 цифры справа налево, затем — аналогично преобразованию из 2-й в 8-ю.

Преобразование из восьмеричной и шестнадцатеричной систем в двоичную:

Перевод из восьмеричной в двоичную — преобразуем каждый разряд восьмеричного числа в двоичное 3-х разрядное число делением на 2 (более подробно о делении см. выше пункт “Преобразование из десятичной системы счисления в другие”), недостающие крайние разряды заполним ведущими нулями.

Для примера рассмотрим число 45₈: 45 = (100) (101) = 100101₂

Перевод из 16-ой в 2-ю — преобразуем каждый разряд шестнадцатеричного числа в двоичное 4-х разрядное число делением на 2, недостающие крайние разряды заполняем ведущими нулями.

Преобразование дробной части любой системы счисления в десятичную:

Преобразование осуществляется также, как и для целых частей, за исключением того, что цифры числа умножаются на основание в степени “-n”, где n начинается от 1.

Пример: 101,011₂ = (1*2² + 0*2¹ + 1*2⁰), (0*2^-1 + 1*2^-2 + 1*2^-3) = (5), (0 + 0,25 + 0,125) = 5,375₁₀

Преобразование дробной части двоичной системы в 8-ую и 16-ую:
Перевод дробной части осуществляется также, как и для целых частей числа, за тем лишь исключением, что разбивка на группы по 3 и 4 цифры идёт вправо от десятичной запятой, недостающие разряды дополняются нулями справа.

Пример: 1001,01₂ = 001 001, 010 = (0*2² + 0*2¹ + 1*2⁰) (0*2² + 0*2¹ + 1*2⁰), (0*2² + 1*2¹ + 0*2⁰) = (0+0+1) (0+0+1), (0+2+0) = 11,2₈

Преобразование дробной части десятичной системы в любую другую:

Для перевода дробной части числа в другие системы счисления нужно обратить целую часть в ноль и начать умножение получившегося числа на основание системы, в которую нужно перевести. Если в результате умножения будут снова появляться целые части, их нужно повторно обращать в ноль, предварительно запомнив (записав) значение получившейся целой части. Операция заканчивается, когда дробная часть полностью обратится в нуль.

Для примера переведем 10,625₁₀ в двоичную систему:

0,625*2 = 1,25

0,250*2 = 0,5

0,5*2 = 1,0

Записав все остатки сверху вниз, получаем 10,625₁₀ = (1010), (101) = 1010,101₂
1.2. Изучение правил перевода чисел в различные системы счисления
Для рассмотрения выберем перевод чисел в наиболее распространенные системы счисления, а именно:

- Двоичную

- Восьмеричную

- Десятичную

- Шестнадцатеричную

Перевод будет осуществляться при помощи трёх функций:

- ROUNDDOWN()

- CONCATENATE()

Функция CONCATENATE объединяет до 255 текстовых строк в одну. Объединяемые элементы могут быть текстом, числами, ссылками на ячейки или сочетанием этих элементов. Например, если в ячейке A1 листа содержится имя человека, а в ячейке B1 — его фамилия, объединить эти два значения в третей ячейке можно с помощью следующей формулы.

Функция ROUNDDOWN округляет число до ближайшего меньшего по модулю значения.

Для перевода числе последовательно будет использоваться функция rounddown для получения остатков от деления которые в дальнейшем будут заноситься в отдельные ячейки и собираться вместе как строка при помощи функции concatenate.

Для этого воспользуемся правилами перевода чисел в различные системы счисления

Пример 1. Перевести СЕ.95₁₆ в двоичную систему счисления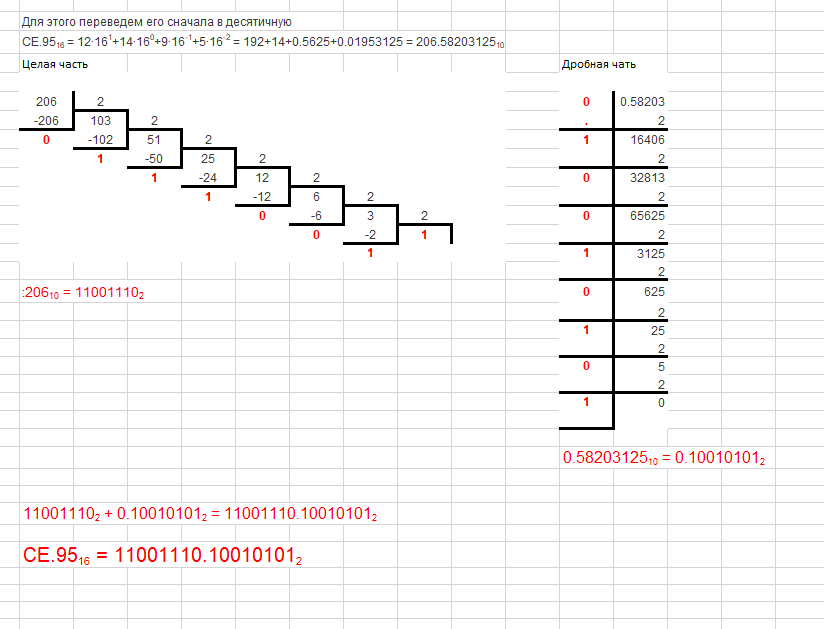


Рисунок 7 – перевод числа СЕ.95₁₆ из шестнадцатеричной системы счисления в двоичную.

Пример 2. Перевести 0.101₂ в десятичную систему счисления


Рисунок 8 – перевод числа 0.101₂ в десятичную систему счисления
Пример 3. Перевести 7883₁₀ в двоичную систему счисления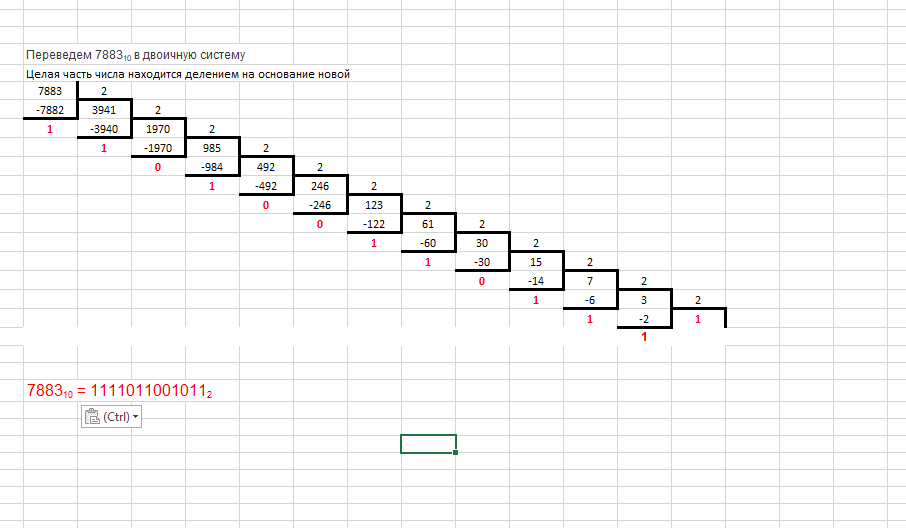


Рисунок 9 – перевод числа 7883₁₀ в двоичную систему счисления
Пример 4. Перевести 24.75₈ в десятичную систему счисления


Рисунок 10 – перевод числа 24.75₈ в десятичную форму

1.3 Образование десятичной системы счисления

В современном русском языке, а также в языках других народов названия всех чисел до миллиона составляются из 37 слов, обозначающих числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 , 12, 13, 14, 15, 16, 17, 18, 19, 20, 30, 40, 50, 60, 70, 80, 90, 100, 200, 300, 400, 500, 600, 700, 800, 900, 1000 (например, восемьсот пятнадцать тысяч триста девяносто четыре). В свою очередь названия этих 37 чисел, как правило, образованы из названий чисел первого десятка (1, 2, 3, 4, 5, 6, 7, 8, 9) и чисел 10, 100, 1000 (например, 18 = восемь на десять, 30 = тридесять и т.д.). В основе этого словообразования лежит число десять, и поэтому наша система наименований называется десятичной системой счисления.

Из упомянутого правила в разных языках имеются различные исключения, объясняющиеся историческими особенностями развития счета. В русском языке единственным исключением является наименование «сорок». Это исключение можно поставить в связь с тем, что число 40 играло некогда особую роль, означая неопределенно большое количество.

В тюркских языках (узбекском, казахском, татарском, башкирском, турецком и др.) исключение составляют наименования чисел 20, 30, 40, 50, тогда как названия чисел 60, 70, 80, 90 образованы из наименований для 6, 7, 8, 9. Во французском языке сохранились недесятичные названия чисел 20 и 80, причем 80 именуется quatrevingt, т.е. «четыре двадцать». Здесь мы имеем остаток древнего двадцатеричного счисления (по числу пальцев на руках и ногах). В латинском языке наименование числа 20 тоже недесятичное (viginti). Наименования чисел 18 и 19 образованы из названия 20 с помощью вычитания: 20–2 и 20–1 (duodeviginti, undeviginti, т.е. «два от двадцати», «один от двадцати»).

2. Разработка программы

Для выполнения цели курсовой работы необходимо реализовать программу, производящую перевод чисел из двоичной системы счисления в десятичную и обратную сторону. Для этого используется язык С++ и IDE Microsoft visual studio 2019.

Структура программы будет выглядеть следующим образом: две функции отвечающие за перевод чисел из десятичной в двоичную систему счисления и из двоичной в десятичную. Сама процедура перевода будет осуществляться с поразрядным занесением числа в массив для дальнейшего его преобразования. После этого пользователю будет выводиться результат перевода в обе системы счисления.

Блок-схема программы и код представлены ниже.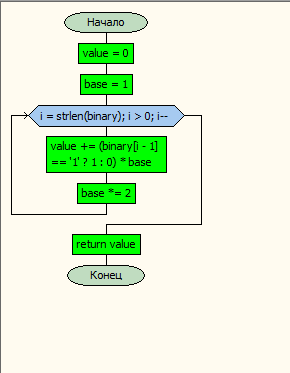


а)


б)


в)

Рис. 11 – блок-схема функций, использующихся при реализации программы

2.1 Структура программы

1. 
   Заголовок
   
2. 
   Подключение дополнительного модуля
   
3. 
   Раздел описания переменных
   
4. 
   Тело программы – блок основных вычислений, включает в себя функции перевода чисел при помощи массивов с поразрядным занесением числа.
   
5. 
   Вывод числа в двух системах счисления.
   

Программа запускается путем нажатия клавиш Shift и F9 в отдельном окне. Необходимо ввести число, которое требуется перевести числа из двоичной в десятичную систему и обратно. После того как вы ввели число на экран будет выведен результат работы программы.

2.2 Код программы и примеры выполнения

#include

#include

#include

using namespace std;

// Возвращает десятичное значение

int bin_to_dec(const char* binary) {

int value = 0;

int base = 1;

for (int i = strlen(binary); i > 0; i--) {

value += (binary[i - 1] == '1' ? 1 : 0) * base;

base *= 2;

}

return value;

}
// Возвращает количество символов двоичного представления

// записанного в binary

int dec_to_bin(int decimal_value, char* binary) {

int current = decimal_value;

int digit_counts = 1;

while (current != 1) {

current /= 2;

digit_counts++;

}

int n = digit_counts;

binary[n] = '\0';

current = decimal_value;

while (current != 1) {

int div = current / 2;

int mod = current - 2 * div;

binary[--n] = mod == 1 ? '1' : '0';

current = div;

}

binary[0] = '1';

return digit_counts;

}

int main()

{

setlocale(LC_ALL, "Rus");

char buf[100];

int value = 0;

cout << "Введите число: ";

cin >> value;

dec_to_bin(value, buf);

cout << "Перевести число " << value << " из двоичной системы счисления в десятичную: " << buf;

cout << endl;

value = bin_to_dec(buf);

cout << "Перевести число " << buf << " из десятичной системы счисления в двоичную: " << value;

return 0;

}



Заключение
По итогу работы можно сказать о достижении следующих результатов:

1. 
   Изучены принципы перевода чисел в различные системы счисления
   
2. 
   Исследованы принципы работы алгоритмов работы различных систем счисления, арифметических операций в них и перевода чисел из одной системы счисления в другую.
   
3. 
   Изучены базовые принципы работы с наиболее распространёнными языкам.
   

Цель работы, заключавшаяся в создании конвертера чисел в различные системы счисления успешно выполнена.

Полученные знания будут использованы в дальнейшем в задачах, связанных с математическими преобразованиями что может быть использовано для работы с алгоритмами шифрования.

Список литературы

1. 
   Кодирование информации (Двоичные коды). Березнюк Н. Т. Андрущенко А. Г. И др. Харьковю 1978.
   
2. 
   Выгодский М.Я. Справочник по элементарной математике, М.: Государственное издательство технико-теоретической литературы, 1956.
   
3. 
   Каган Б.М. Электронные вычислительные машины и системы, М.: Энергоатомиздат, 1985.
   
4. 
   Майоров С.А., Кириллов В.В., Приблуда А.А., Введение в микроЭВМ, Л.: Машиностроение, 1988.
   
5. 
   Фомин С.В. Системы счисления, М.: Наука, 1987.
   
6. 
   Ролич Ч. Н. – От 2 до 16, Минск, «Высшая школа», 1981г.
   
7. 
   Математическая энциклопедия. М: “Советская энциклопедия” 1985г.
   
8. 
   Шауман А. М. Основы машинной арифметики. Ленинград, Издательство Ленинградского университета. 1979г.