КУРСОВОЙ ПРОЕКТ ПО ДИСЦИПЛИНЕ «ДЕТАЛИ МАШИН» Тема: спроектировать привод цепного конвейера. КУРСОВАЯ. Курсовой проект по дисциплине детали машин
 Скачать 279.14 Kb. Скачать 279.14 Kb.
|
|
2 Расчёты зубчатых цилиндрических передач 2.1 Выбор материалов для зубчатых колёс Выбираем сталь как для колеса(2) (Колесо 45 ), так и для шестерни(1)(Шестерня 45). Механические свойства стали (табл. 2.1) Таблица 2.1. Механические свойства стали 45
Шестерня 45, НВ=170 Колесо 45, НВ=170 2.2 Расчёт допускаемых напряжений 2.2.1 Допускаемые контактные напряжения Допускаемые контактные напряженияσНР , МПа, определяют по формуле σНР = 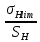 ZRZυKLKχH , (2.1) ZRZυKLKχH , (2.1)где σНlim — предел контактной выносливости поверхностей зубьев, соответствующий эквивалентному числу циклов перемены напряжения NH0, МПа; SH — коэффициент безопасностипри расчёте зубьев на контактную выносливость активных поверхностей зубьев, SH = 1,1; ZR— коэффициент, учитывающий шероховатость сопряженных поверхностей зубьев, общий для шестерни и колеса, ZR = 1 при 7 классе степени точности; Zυ— коэффициент, учитывающий окружную скорость, первоначально принимается, Zυ= 0,8 KL— коэффициент, учитывающий влияние смазки, KL = 1; KχH— коэффициент, учитывающий размеры зубчатого колеса, первоначально принимается KχH = 1. Предел контактной выносливости σНlim, МПа, определяют по формуле: σНlim = σНlimbKHL, (2.2) где σНlimb — предел контактной выносливости поверхностей зубьевсоответствующий базовому числу циклов перемены напряжения NH0; KHL— коэффициент долговечности; NHE— эквивалентное число циклов перемены напряжений, посчитано ранее. При расчете косозубых передач принимают усредненное значение, полученное для шестерни и колеса передачи по формуле: σНР = 0,45 ( σН Р 1 + σН Р 2 ) , (2.3) Базовое число циклов перемены напряжений: NH0= 30 × 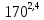 = 6, 76× 106 . = 6, 76× 106 . Коэффициент долговечности: KHL= 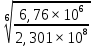 = 0,55 . = 0,55 . Предел контактной выносливости поверхностей зубьевсоответствующий базовому числу циклов перемены напряжения: σНlimb = 2 ×170 + 70 = 410 МПа. Предел контактной выносливости: σНlim = 410× 0,55= 225, 5 МПа. Допускаемые контактные напряжения для шестерни: σНР1 = 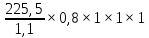 = 164 МПа . = 164 МПа . Так как материал шестерни и колеса один и тот же, их допускаемые контактные напряжения будут идентичны: σНР2 = σНР 1 , σНР2 = 164 МПа , Усредненное значение допускаемых контактных напряжений: σНР = 0,45 (164+ 164) = 147, 6 МПа . 2.2.2 Допускаемые напряжения при расчёте на выносливость зубьев при изгибе (Шестерня) Допускаемые напряжения определяют по формуле: σFР = 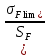 YSYRKχF ,(2.4) YSYRKχF ,(2.4)где σFlim — предел выносливости зубьев при изгибе, соответствующий эквивалентному числу циклов перемены напряжения NH0, МПа; SF — коэффициент безопасностипри расчёте зубьев на выносливость при изгибе, формула; YS— коэффициент, учитывающий градиент напряжений и чувствительность материала к концентрации напряжений, первоначально принимается YS =1; YR— коэффициент, учитывающий шероховатость переходной поверхности для шлифования и зубофрезерования, YR = 1; KχF— коэффициент, учитывающий размеры зубчатого колеса, первоначально принимается KχF = 1 Предел контактной выносливости зубьев при изгибе σFlim , МПа, определяют по формуле : σFlim = 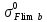 KFcKFL , (2.5) KFcKFL , (2.5)где 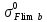 — предел выносливости зубьев при изгибе, соответствующий — предел выносливости зубьев при изгибе, соответствующий базовому числу циклов перемены напряжения, МПа; KFc — коэффициент, учитывающий влияние двухстороннего приложения нагрузки, при одностороннем приложении нагрузки (конвейеры) KFc = 1; KFL— коэффициент долговечности, примем KFL= 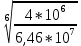 = 0,63. = 0,63.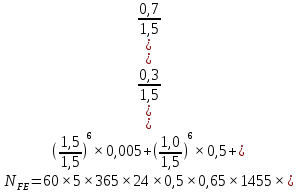 = 6,46× = 6,46×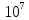 . .SF = 1,75 × 1= 1,75 , Предел выносливости зубьев при изгибе, соответствующий базовому числу циклов перемены напряжения: 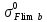 = 1,8 ×170 = 306 МПа , = 1,8 ×170 = 306 МПа , Предел контактной выносливости зубьев при изгибе σFlim =306×1×0,63 = 192, 78 МПа , Допускаемые напряжения: σFР1 = 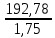 1× 1×1 = 110, 16 МПа . (расчет для колеса такой-же (σFР2=110,167) ) 1× 1×1 = 110, 16 МПа . (расчет для колеса такой-же (σFР2=110,167) ) Теперь проведем расчёты зубчатой передачи на прочность. Начинать расчет будем с первой (быстроходной) ступени. 2.3 Расчёт зубчатой передачи на прочность для тихоходной ступени 2.3.1 Расчёт передачи на контактную прочность Предварительно размер межосевого расстояния цилиндрической передачиступени, мм, определяют по формуле: αW = Kα ( U + 1 ) 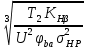 , (2.6) , (2.6)где Kα — вспомогательный коэффициент, для косозубой передачи Kα=4; U — передаточное отношение ступени редуктора, U =4; T2 — крутящий момент на ведущем валу ступени редуктора,Н∙м (рассчитано ранее); 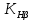 — коэффициент, учитывающий распределение нагрузки по ширине — коэффициент, учитывающий распределение нагрузки по ширине венца; φbd — вспомогательный параметр отношения рабочей ширины зубчатого венца зубчатого колеса ступени редуктора к начальному диаметру шестерни; этот параметр связан с αW, φbd = bW / dW1 = 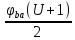 ; ;φba — вспомогательный параметр отношения рабочей ширины зубчатого венца зубчатого колеса ступени редуктора кαW; предварительно задается из диапазона 0,315; 0,4; 0,5; принимаем φba = 0,4; φbd = 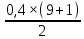 = 2 , = 2 , 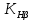 = 1,45 , = 1,45 , Размер межосевого расстояния для быстроходной ступени: αW1 = 4 ( 9 + 1 ) 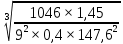 = 554,8 мм , = 554,8 мм ,Согласовываем полученное значение со стандартными, принимаем αW1 =560 мм . Значение модуля, мм, ступени выбирается по зависимости: mn = 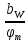 = φba = φba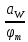 , (2.7) , (2.7)где φm — вспомогательный параметр отношения рабочей ширины зубчатого венца зубчатого колеса к модулю ступени редуктора, φm = 25; Значение модуля для тихоходной ступени: mn1 =0,4 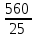 = 8,9 мм = 8,9 мм Согласовываем полученное значение со стандартными принимаем mn1 =9 мм . Суммарное число зубьев, округляемое до целого значения, определяют по формуле: ZΣ = 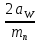 cos ( β) , (2.8) cos ( β) , (2.8)где β — угол наклона зубьев косозубой передачи, β = 8… 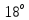 , принимаем , принимаем β= 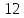 ; ;ZΣ = 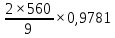 = 121,7, = 121,7, округляем до 122. Уточняем угол наклона зубьев по формуле: β = arccos( 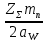 ) , (2.9) ) , (2.9)β = arccos( 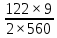 ) = 0,198. ) = 0,198. Числа зубьев колес, округленные до целого значения, рассчитывают для шестерни и колеса: Z1= 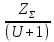 ;Z2 = ZΣ - Z1; (2.10) ;Z2 = ZΣ - Z1; (2.10)Z1 = 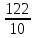 = 12,2 = 12,2 округляем до 12. Z2 = 122 – 12 = 110 . 2.3.2 Геометрические параметры и окружная скорость зубчатых колес Диаметры делительных окружностей, мм: d1 = 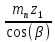 ;d2 = ;d2 = 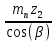 ; (2.11) ; (2.11)d1 = 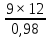 = 110 мм , = 110 мм , d2 = 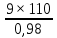 = 1010 мм. = 1010 мм. Диаметры окружности вершин зубьев, мм: da1 = d1 + 2mn ; da2 = d2 + 2mn ; (2.12) da1 = 110+ 2×9 =128 мм , da2 = 1010 + 2×9 =1028 мм . Диаметры окружности впадин зубьев, мм: df1 = d1-2,5mn ; df2 = d2- 2,5mn ; (2.13) df1 = 110 – 2,5 ×9 =87,5 мм , df2 = 1010 – 2,5 ×9 =987,5 мм . Ширина венцов зубчатого колеса и шестерни ступени, мм: b2 = φbaaW ; b1 = b2 + 5 ; (2.14) b2 = 0,4×560 =224 мм , b1 = 224 + 5 = 229 мм. Окружная скорость, м/с, определяется по формуле V = 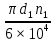 ; (2.15) ; (2.15)V = 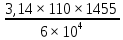 = 8, 375 м/с . = 8, 375 м/с .2.3.3 Расчёт передачи на выносливость зубьев при изгибе Расчет позволяет предотвратить возможность усталостного излома зубьев. Производится для менее прочного из колес передачи. Для шестерни и колеса подсчитывают отношение допускаемого напряжения на изгиб к коэффициенту форму зуба YFв зависимости от эквивалентного числа зубьев ZV : ZV = 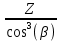 . (2.16) . (2.16)Определяются отношения 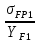 и и 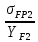 . Если . Если 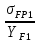 < <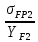 , необходимо проверять на изгиб зубья шестерни и в формулу (2.18) – см. ниже – подставлять значения YF = YF1и , необходимо проверять на изгиб зубья шестерни и в формулу (2.18) – см. ниже – подставлять значения YF = YF1и σFP = σFP1. Если 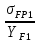 > >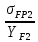 необходимо проверять на изгиб зубья колеса и в формулу (2.18) подставляются значения YF = YF2и σFP = σFP2 . необходимо проверять на изгиб зубья колеса и в формулу (2.18) подставляются значения YF = YF2и σFP = σFP2 .Эквивалентное число зубьев ZV для шестерни: ZV1 = 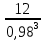 = 12, 74, = 12, 74, для колеса ZV2 = 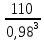 = 116, 87 . = 116, 87 . Коэффициент формы зуба YFдля шестерни: YF1 = 4,1 , для колеса: YF2 = 4,4 . Определяем отношения 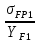 и и 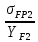 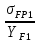 = = 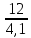 , , 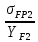 = = 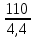 , , 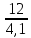 < <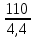 , , 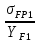 < <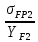 , , следовательноYF = YF1 и σFP = σFP1 . Возникающие изгибные напряжения σF , МПа, выражаются формулой: σF = 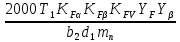 ≤σFP , (2.17) ≤σFP , (2.17)где T1 — крутящий момент на промежуточном валу ступени редуктора,Н∙м (рассчитано ранее);T1 =121, 4 Н*м KFα — коэффициент, учитывающий распределение нагрузки между зубьями; KFβ — коэффициент, учитывающий распределение нагрузки по ширине венца; KFV — коэффициент, учитывающий влияние динамической нагрузки; Yβ — коэффициент, учитывающий наклон зубьев. KFβ = 1,85 . Коэффициент, учитывающий наклон зубьев: Yβ = 1 . Коэффициент торцового перекрытия: εα = [1,88 – 3,2 ( 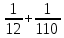 )] )]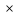 0,98= 1, 26 . 0,98= 1, 26 . Коэффициент, учитывающий распределение нагрузки между зубьями: KFα = 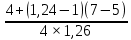 = 0,89 . = 0,89 . Коэффициент, учитывающий влияние динамической нагрузки: KFV = 1 + 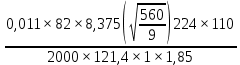 = 4,26 . = 4,26 .σF = 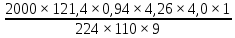 = 17, 53 МПа = 17, 53 МПа17,53<110 | ||||||||||
