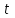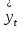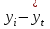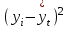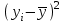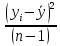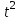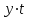Курсовая. Патрушев. Курсовой проект по дисциплине Государственный пожарный надзор
 Скачать 0.58 Mb. Скачать 0.58 Mb.
|
Выводы по главе 1В первой главе было рассмотрено правовое регулирование в области Федерального государственного пожарного надзора. Основными нормативно-правовыми актами, регулирующими деятельность органов федерального государственного пожарного надзора, являются: Федеральный закон от 21 декабря 1994 года № 69-ФЗ "О пожарной безопасности"; Федеральный закон от 31.07.2020 № 248-ФЗ «О государственном контроле (надзоре) и муниципальном контроле в Российской Федерации»; Федеральный закон от 22 июля 2008 года № 123-ФЗ «Технический регламент о требованиях пожарной безопасности»; Постановление Правительства Российской Федерации от 12 апреля 2012 года № 290 «О федеральном государственном пожарном надзоре»; Постановление Правительства Российской Федерации от 16 сентября 2020 года № 1479 «Об утверждении правил противопожарного режима в Российской Федерации». Также была рассмотрена инфраструктура Петродворцового района города Санкт-Петербург и структура системы обеспечения пожарной безопасности муниципального образования. В заключение первой главы была рассмотрена организация и основные направления деятельности территориального надзорного органа МЧС России по осуществлению федерального ГПН. ГЛАВА 2 ИССЛЕДОВАНИЕ ДЕЯТЕЛЬНОСТИ ТЕРРИТОРИАЛЬНОГО НАДЗОРНОГО ОРГАНА МЧС РОССИИ ПО ОСУЩЕСТВЛЕНИЮ ФЕДЕРАЛЬНОГО ГПН2.1 Анализ результативности деятельности территориального надзорного органа МЧС России по осуществлению федерального ГПНПриказом МЧС России от 21 ноября 2008 года №714 «Об утверждении порядка учета пожаров и их последствий» утвержден порядок учета пожаров и их последствий. Показателями, характеризующими состояние обстановки с пожарами и их последствиями являются: количество пожаров, единиц; число погибших людей при пожарах, человек; число травмированных людей при пожарах, человек; материальный ущерб от пожаров, рублей. Анализ результативности деятельности территориального надзорного органа МЧС России по осуществлению федерального государственного пожарного надзора включает в себя: статистический анализ и прогноз количества пожаров на объектах защиты и причин их возникновения; статистический анализ и прогноз числа погибших людей при пожарах, обстоятельств и причин их гибели; статистический анализ и прогноз числа травмированных людей при пожарах, обстоятельств и причин их травмирования статистический анализ и прогноз материального ущерба от пожаров. 2.1.1 Статистический анализ и прогноз количества пожаров на объектах защиты и причин их возникновенияПо данным с 2016 по 2020 годы в Петродворцового районе города Санкт-Петербурга зарегистрировано: 2016 год – 274 пожаров; 2017 год – 258 пожаров; 2018 год – 105 пожаров; 2019 год – 381 пожаров; 2020 год – 360 пожаров. 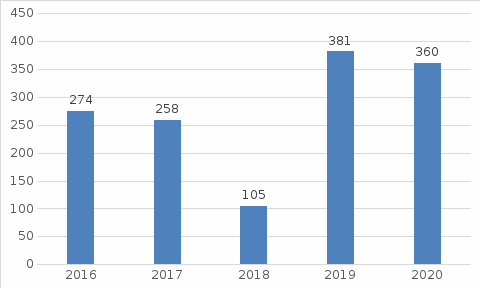 Рисунок 2 – Количество пожаров Вывод: Анализ статистических данных о количестве пожаров в Петродворцовом районе за 2016-2020 г. показывает, что: Количество пожаров в Российской Федерации за последние 2 года увеличилось примерно в 4 раза. Это связано с введением приказа МЧС России от 8 октября 2018 года №431 «О внесении изменений в Порядок учета пожаров и их последствий, утвержденный приказом МЧС России от 21 ноября 2008 года, №714». В данном приказе были внесены изменения по учету числа пожаров и пострадавших. Основными причинами возникновения пожаров в рассматриваемом районе являются: неосторожное обращение с огнем, в том числе неосторожное обращение с огнем при курении; детская шалость; поджоги; аварийный режим работы электрических сетей и оборудования. Наиболее эффективным способом выявления тенденции ряда динамики является аналитическое выравнивание. Графическая интерпретация прогноза имеет вид функции распределения анализируемого показателя деятельности территориального органа ГПН по исследуемым временным интервалам t. Итак, приступим к прогнозу показателей обстановки с пожарами в Петродворцовом районе. Таблица 1-Прогнозирование*/ количества пожаров
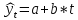 (1) (1)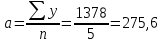 (2) (2)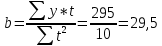 (3) (3)Уравнение прямой, представляющее собой трендовую модель искомой функции, будет иметь вид: 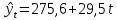 Подставляя в данное уравнение последовательно значения t, равные -2, -1, 0, 1, 2, находим выровненные значения 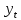 . Если расчеты выполнены правильно то . Если расчеты выполнены правильно то 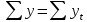 . В данном расчете они равны 2007. Следовательно, значения уровней выровненного ряда найдены верно. . В данном расчете они равны 2007. Следовательно, значения уровней выровненного ряда найдены верно.Проверка адекватности полученного прогностического уравнения Важным моментом получения прогноза является оценка достоверности полученного результата. Для этой цели используем корреляционное отношение: 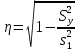 (4) (4)где 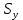 стандартная ошибка, вычисляемая по формуле: стандартная ошибка, вычисляемая по формуле: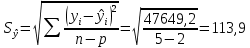 (5) (5)где 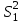 - полная дисперсия зависимой переменной: - полная дисперсия зависимой переменной: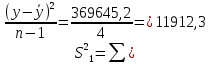 (6) (6)где 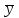 - средняя арифметическая зависимой переменной, вычисляемая по эмпирическим данным ряда. - средняя арифметическая зависимой переменной, вычисляемая по эмпирическим данным ряда.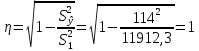 Поскольку 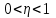 , то близость коэффициента множественной корреляции к единице позволяет судить одновременно о надежности модели и существенности связи между переменными. , то близость коэффициента множественной корреляции к единице позволяет судить одновременно о надежности модели и существенности связи между переменными. По данным таблицы на основе исчисленного уравнения экстраполяцией при t=3 можно определить ожидаемое количество пожаров в 2021 году: 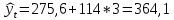 На практике результат экстраполяции прогнозируемых явлений обычно получают не точечными (дискретными), а интервальными оценками. Для определения границ интервалов: 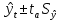 (7) (7)где 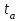 - коэффициент доверия по распределению Стьюдента (2,776); - коэффициент доверия по распределению Стьюдента (2,776);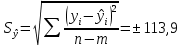 - остаточное среднее квадратичное отклонение от тренда, скорректированное по числу степеней свободы (n-m); n – число уровней ряда динамики; m – число параметров адекватной модели тренда (для уравнения прямой m= 2). - остаточное среднее квадратичное отклонение от тренда, скорректированное по числу степеней свободы (n-m); n – число уровней ряда динамики; m – число параметров адекватной модели тренда (для уравнения прямой m= 2).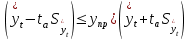 (8) (8)Зная точечную оценку прогнозируемого значения количества пожаров определяем вероятностные границы интервала: 364,1-2,77  113,9 yп р 364,1+2,77 113,9 yп р 364,1+2,77 113,9 113,947,803 yп р 680,396 Это значит, что в 2021 году, количество пожаров может быть от 48до 681. Вывод: Следовательно, можно утверждать, что количество пожаров в Петродворцовом районе г. Санкт – Петербурга в 2021 в среднем составит 365, а достоверность данного прогноза составляет 0,85, что является оптимальным для достоверности данного прогноза.  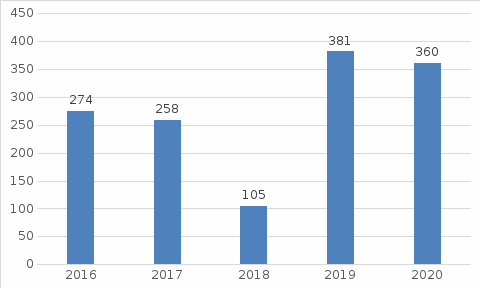 Рисунок 3 – Прогнозирование количества пожаров 2.1.2 Статистический анализ и прогноз количества погибших людей при пожарах, обстоятельств и причин их гибелиВ период с 2016 по 2020 число погибших распределилось так: 2016 год -17 человек; 2017 год - 16 человек; 2018 год - 6 человек; 2019 год – 6 человек; 2020 год – 5 человек. 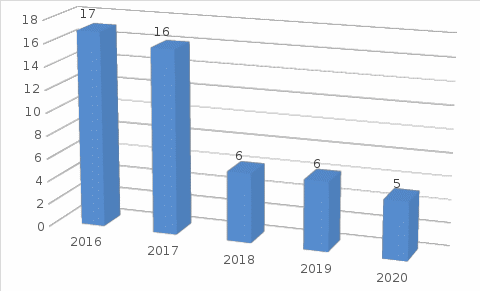 Рисунок 4 - Количество людей погибших на пожаре за 2016-2020 годы. Исходные данные о количестве погибших людей в исследуемом пятилетнем периоде были приведены на рисунке 4. Таблица 2-Прогнозирование количества погибших
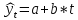 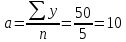 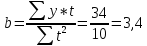 Уравнение прямой, представляющее собой трендовую модель искомой функции, будет иметь вид: 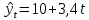 Подставляя в данное уравнение последовательно значения t, равные -2, -1, 0, 1, 2, находим выровненные значения 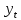 . Если расчеты выполнены правильно то . Если расчеты выполнены правильно то  . В данном расчете они равны 50. Следовательно, значения уровней выровненного ряда найдены верно. . В данном расчете они равны 50. Следовательно, значения уровней выровненного ряда найдены верно.Проверка адекватности полученного прогностического уравнения Важным моментом получения прогноза является оценка достоверности полученного результата. Для этой цели используем корреляционное отношение: 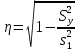 где 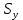 стандартная ошибка, вычисляемая по формуле: стандартная ошибка, вычисляемая по формуле: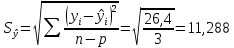 где 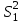 - полная дисперсия зависимой переменной: - полная дисперсия зависимой переменной: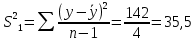 где 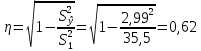 Поскольку По данным таблицы на основе исчисленного уравнения экстраполяцией при t=3 можно определить ожидаемое количество пожаров в 2021 году: 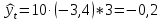 На практике результат экстраполяции прогнозируемых явлений обычно получают не точечными (дискретными), а интервальными оценками. Для определения границ интервалов: 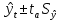 где 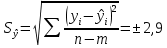 - остаточное среднее квадратичное отклонение от тренда, скорректированное по числу степеней свободы (n-m); n – число уровней ряда динамики; m – число параметров адекватной модели тренда (для уравнения прямой m= 2). - остаточное среднее квадратичное отклонение от тренда, скорректированное по числу степеней свободы (n-m); n – число уровней ряда динамики; m – число параметров адекватной модели тренда (для уравнения прямой m= 2).Вероятностные границы интервала прогнозируемого явления:  Зная точечную оценку прогнозируемого значения количества пожаров определяем вероятностные границы интервала: -0,2–2,776·2,9 ≤ yп р ≤ -0,2+2,776·2,9 -8,43 ≤ yп р ≤ 8,03 Вывод: опираясь на полученные значения в ходе расчета, можно прийти к выводу, что с вероятностью 23% количество погибших людей в Петродворцовом районе, в 2021 году не снизится по сравнению с 2020 годом и будет составлять не более 8. 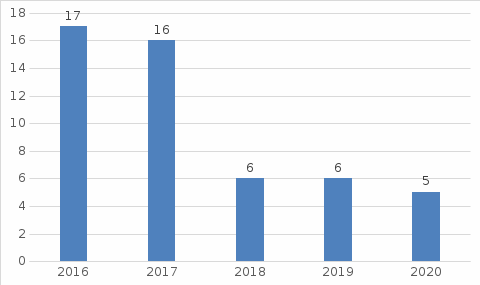 Рисунок 5 – Прогнозирование количества погибших 2.1.3 Статистический анализ и прогноз количества травмированных людей при пожарах, обстоятельств и причин их травмированияКоличество травмированных в период 2016 – 2020 годов составило: 2016 год – 35 человек; 2017 год - 32; 2018 год - 5; 2019 - 15; 2020 год - 15. 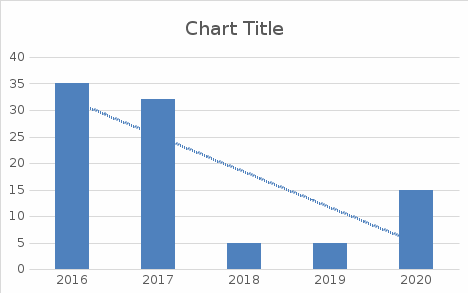 Рисунок 6 - Количество людей травмированных на пожаре за 2016-2020 годы. Исходные данные о количестве травмированных людей в исследуемом пятилетнем периоде были приведены на рисунке 6. Таблица 3-Прогнозирование количества пострадавших
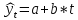 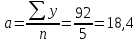 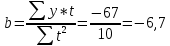 Уравнение прямой, представляющее собой трендовую модель искомой функции, будет иметь вид: 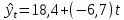 Подставляя в данное уравнение последовательно значения t, равные -2, -1, 0, 1, 2, находим выровненные значения 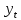 . Если расчеты выполнены правильно то . Если расчеты выполнены правильно то 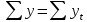 . В данном расчете они равны 92. Следовательно, значения уровней выровненного ряда найдены верно. . В данном расчете они равны 92. Следовательно, значения уровней выровненного ряда найдены верно.Проверка адекватности полученного прогностического уравнения Важным моментом получения прогноза является оценка достоверности полученного результата. Для этой цели используем корреляционное отношение: 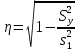 где 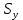 стандартная ошибка, вычисляемая по формуле: стандартная ошибка, вычисляемая по формуле: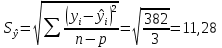 где 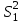 - полная дисперсия зависимой переменной: - полная дисперсия зависимой переменной: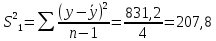 где 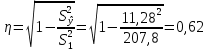 Поскольку По данным таблицы на основе исчисленного уравнения экстраполяцией при t=3 можно определить ожидаемое количество пожаров в 2021 году: 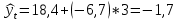 На практике результат экстраполяции прогнозируемых явлений обычно получают не точечными (дискретными), а интервальными оценками. Для определения границ интервалов: 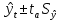 где 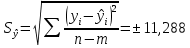 - остаточное среднее квадратичное отклонение от тренда, скорректированное по числу степеней свободы (n-m); n – число уровней ряда динамики; m – число параметров адекватной модели тренда (для уравнения прямой m= 2). - остаточное среднее квадратичное отклонение от тренда, скорректированное по числу степеней свободы (n-m); n – число уровней ряда динамики; m – число параметров адекватной модели тренда (для уравнения прямой m= 2).Вероятностные границы интервала прогнозируемого явления:  Зная точечную оценку прогнозируемого значения количества пожаров определяем вероятностные границы интервала: -1,7–2,776·11,288 ≤ yп р ≤ 23,1+2,776·3,40 33,03 ≤ yп р ≤ 29,63 Вывод: опираясь на полученные значения в ходе расчета, можно прийти к выводу, что количество травмированных людей в Петродворцовом районе, в 2021 году увеличится по сравнению с 2020 годом и будет составлять 32 человек , но не более 33 человек.  Рисунок 7 – Прогнозирование количества пострадавших 2.1.4 Статистический анализ и прогноз прямого материального ущерба от пожаровВ период с 2016 по 2020 год размер ущерба от пожаров составил: 2016 год – 9224 т.р.; 2017 год – 11236 т.р.; 2018 год – 12597 т.р., 2019 год – 265 т.р., 2020 год – 88728 т.р. 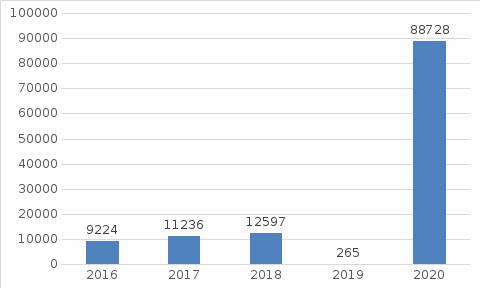 Рисунок 8 - Размер ущерба от пожаров за 2016-2020 годы. Исходные данные о материальных потерях в исследуемом пятилетнем периоде были приведены на рисунке 8. Таблица 4-Прогнозирование материального ущерба
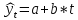 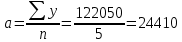 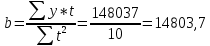 Уравнение прямой, представляющее собой трендовую модель искомой функции, будет иметь вид: 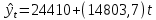 Подставляя в данное уравнение последовательно значения t, равные -2, -1, 0, 1, 2, находим выровненные значения  . Если расчеты выполнены правильно то . Если расчеты выполнены правильно то  . В данном расчете они равны 122050. Следовательно, значения уровней выровненного ряда найдены верно. . В данном расчете они равны 122050. Следовательно, значения уровней выровненного ряда найдены верно.Проверка адекватности полученного прогностического уравнения Важным моментом получения прогноза является оценка достоверности полученного результата. Для этой цели используем корреляционное отношение: 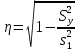 где 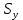 стандартная ошибка, вычисляемая по формуле: стандартная ошибка, вычисляемая по формуле: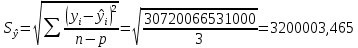 где 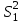 - полная дисперсия зависимой переменной: - полная дисперсия зависимой переменной: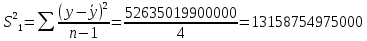 где 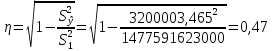 Поскольку По данным таблицы на основе исчисленного уравнения экстраполяцией при t=3 можно определить ожидаемое количество пожаров в 2021 году: 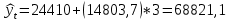 На практике результат экстраполяции прогнозируемых явлений обычно получают не точечными (дискретными), а интервальными оценками. Для определения границ интервалов: 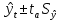 где 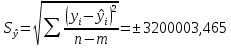 остаточное среднее квадратичное отклонение от тренда, скорректированное по числу степеней свободы (n-m); n – число уровней ряда динамики; m – число параметров адекватной модели тренда (для уравнения прямой m= 2). остаточное среднее квадратичное отклонение от тренда, скорректированное по числу степеней свободы (n-m); n – число уровней ряда динамики; m – число параметров адекватной модели тренда (для уравнения прямой m= 2).Вероятностные границы интервала прогнозируемого явления:  Зная точечную оценку прогнозируемого значения количества пожаров определяем вероятностные границы интервала: 68821,1–2,776·3200003,465≤ yп р ≤ 68821,1+2,776·3200003,465 -8814388,519≤ yп р ≤8952030,719 Вывод: Следовательно, материальный ущерб от пожаров в Петродворцовом районе г. Санкт – Петербурга в 2021 в среднем составит 8052030,719 тыс.руб., а достоверность данного прогноза составляет 0,71, что является не оптимальным для достоверности данного прогноза. 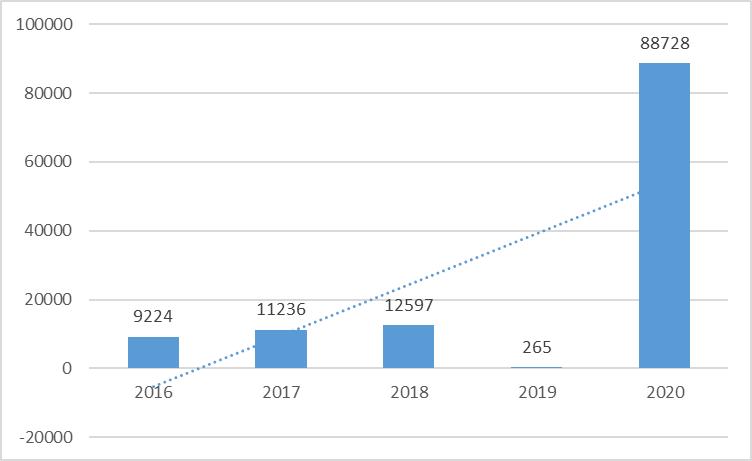 Рисунок 9 – Прогнозирование материального ущерба | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||