Курсовой проект по дисциплине Основы теории надежности тема работы Методы расчета показателей надежности сжат
 Скачать 428.29 Kb. Скачать 428.29 Kb.
|
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА Федеральноегосударственное бюджетное образовательное учреждение высшего образования «Петербургский государственный университет путей сообщения Императора Александра I» (ФГБОУ ВО ПГУПС) Факультет «Автоматизация и интеллектуальные технологии» Кафедра «Автоматика и телемеханика на железных дорогах» КУРСОВОЙ ПРОЕКТ по дисциплине «Основы теории надежности» ТЕМА РАБОТЫ: «Методы расчета показателей надежности СЖАТ» Выполнил:
Санкт-Петербург 2022 1. Статистические оценки показателей надежностиВариант 4 На основании статистической выборки из 30 значений построить гистограмму частот. Используя критерий Пирсона, убедиться в экспоненциальном законе распределения времени наработки до отказа t. Построить теоретическую функцию плотности распределения a(t). Таблица 1 – статистика отказавших реле.
Диапазон значений случайной величины: 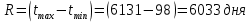 Количество интервалов К: 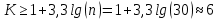 Интервалы 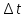 : :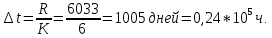 Определение частоты попадания в i-й интервал: 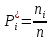 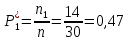 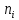 – число попаданий в i-й интервал; – число попаданий в i-й интервал;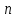 – число попаданий в i-й интервал. – число попаданий в i-й интервал.Статистическая плотность вероятности времени безотказной работы: 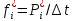 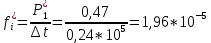 Результаты сведем в таблицу 2 Таблица 2
Теоретическая функция частоты отказов: 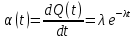 Среднее время наработки до отказа: 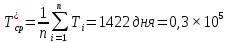 ч чИнтенсивность отказов: 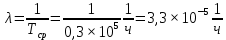 Формула теоретического числа попаданий в i-й интервал: 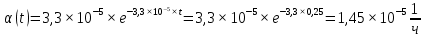 Используя полученное значение интенсивности отказов 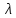 , найдем значения частоты отказов для заданных значений времени наработки ti . Эти значения представлены в 7-й строке таблицы 2. Теоретическая кривая функции плотности распределения времени наработки до отказа (частота отказов) представлена на рис. 2 пунктирной линией. , найдем значения частоты отказов для заданных значений времени наработки ti . Эти значения представлены в 7-й строке таблицы 2. Теоретическая кривая функции плотности распределения времени наработки до отказа (частота отказов) представлена на рис. 2 пунктирной линией. Далее, найдем теоретическое число попаданий в i-й интервал: 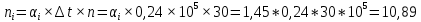 Значения теоретического числа попаданий в i-й интервал 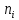 представлено в 8-й строчке таблицы 2. представлено в 8-й строчке таблицы 2.Мера расхождения между теоретическими числами 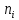 и экспериментальными и экспериментальными 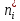 : :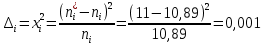 Просуммировав значения этого ряда, найдем значение 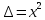 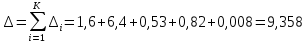 Число степеней свободы: 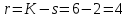 Из таблицы 3 находим вероятность 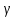 = 0,03. Это значение не превышает порог = 0,03. Это значение не превышает порог 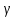 = 0,3, что говорит о несогласии экспериментальных данных с гипотезой об экспоненциальном законе распределения времени наработки до отказа. = 0,3, что говорит о несогласии экспериментальных данных с гипотезой об экспоненциальном законе распределения времени наработки до отказа.Таблица 3 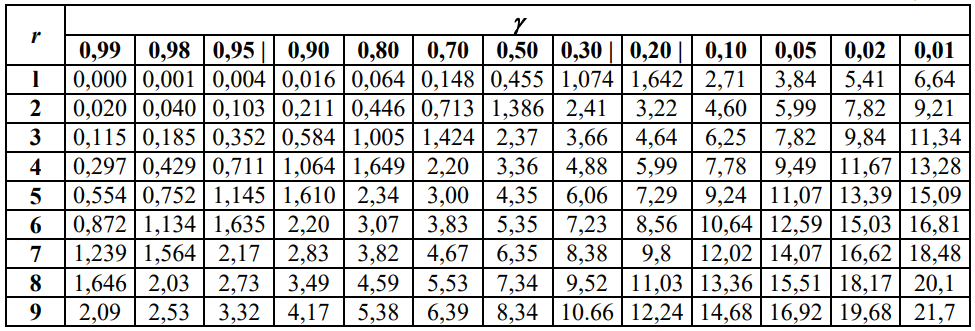 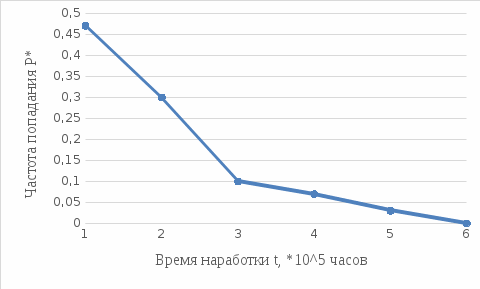 Рисунок 1. График полигона (частота попадания в заданный интервал). 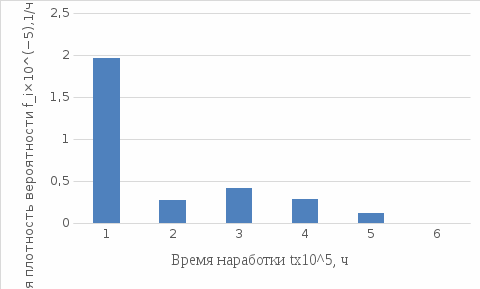 Рисунок 2. Гистограмма (статистическая плотность распределения). 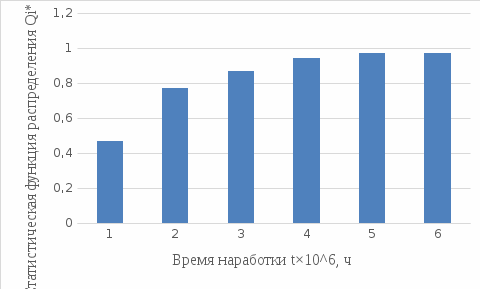 Рисунок 3. Статистическая функция распределения Вывод: получен теоретический поток отказов 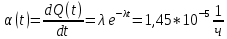 с параметром интенсивности потока отказов с параметром интенсивности потока отказов 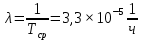 . При проверке гипотезы, получено, что экспериментальные данные не согласуются с гипотезой об экспоненциальном законе распределения времени наработки до отказа, из чего следует, что распределение экспериментальных данных соответствует экспоненциальному закону. . При проверке гипотезы, получено, что экспериментальные данные не согласуются с гипотезой об экспоненциальном законе распределения времени наработки до отказа, из чего следует, что распределение экспериментальных данных соответствует экспоненциальному закону.Статистическая оценка параметров надежности восстанавливаемых устройств На предприятии в момент времени 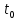 =0 было установлено =0 было установлено 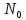 восстанавливаемых устройств. При проверках на промежутках времени восстанавливаемых устройств. При проверках на промежутках времени 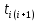 (i = 0, 1, 2) подсчитывалось, сколько устройств отказало на данном промежутке (i = 0, 1, 2) подсчитывалось, сколько устройств отказало на данном промежутке 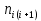 и сколько было восстановлено и сколько было восстановлено 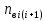 . Найти статистические параметры безотказности и ремонтопригодности на заданном промежутке времени. . Найти статистические параметры безотказности и ремонтопригодности на заданном промежутке времени. Рисунок 4. Таблица 4
Пусть на предприятии в момент времени t0=0 было установлено N0=400 восстанавливаемых устройств, например, лампочек. При проверках на промежутках времени ti(i+1) подсчитывалось, сколько устройств отказало на данном промежутке ni(i+1) и сколько было восстановлено nвi(i+1). Пусть за t02=4 месяца, сгорело n12= 12 лампочек, а успели заменить nв12= 12 лампочек. Найдем статистические оценки параметров безотказности и ремонтопригодности. Вероятность безотказной работы: 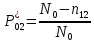 = (400-12)/400=0,97 = (400-12)/400=0,97Вероятность отказа: 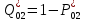 =1- 0,97=0,03 =1- 0,97=0,03Частоту отказов можно найти по формуле: 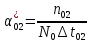 = =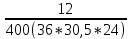 =1,12* =1,12* 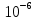 , 1/ч , 1/чИнтенсивность отказов находим по формуле: 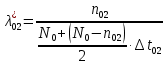 = =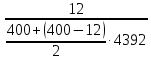 =6,93* =6,93*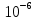 , 1/ч , 1/ч Параметр потока отказов можно оценить по формуле: 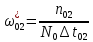 = =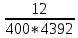 =6,83* =6,83*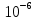 1/ч 1/чДалее найдем показатели ремонтопригодности. Вероятность восстановления находим по формуле: 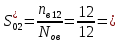 1 1Частоту восстановления и интенсивность восстановления найдем по формуле: 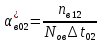 = =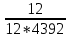 = =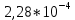 1/ч 1/ч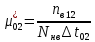 = = 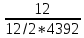 =4,6* =4,6*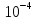 1/ч 1/чВывод: статистические параметры безотказности и ремонтопригодности на заданном промежутке времени равны: Показатели безотказности: Вероятность отказа: 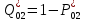 =0,03 =0,03Вероятность безотказной работы: 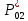 =0,97 =0,97Частота отказов: 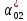 =1,12* =1,12* 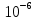 1/ч 1/чИнтенсивность отказов : 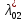 =6,93* =6,93*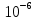 1/ч 1/ч Параметр потока отказов: 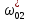 =6,83* =6,83*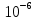 1/ч 1/чПоказатели ремонтопригодности: Вероятность восстановления: 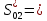 1 1Частота восстановления: 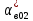 = =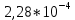 1/ч 1/чИнтенсивность восстановления: 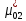 = 4,6* = 4,6*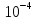 1/ч 1/ч | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

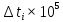 ,ч
,ч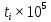 ,ч
,ч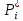
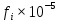 ,1/ч
,1/ч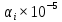 ,1/ч
,1/ч