Курсовой проект по дисциплине Основы теории надежности тема работы Методы расчета показателей надежности сжат
 Скачать 428.29 Kb. Скачать 428.29 Kb.
|
4. Расчет показателей надежности восстанавливаемых систем методом марковских процессовРабота некоторого устройства характеризуется графом, представленным на рисунке 1. При этом S0 – исправное состояние, S1, S2, S3 – работоспособные состояния с различными неисправностями, S4 – неработоспособное состояние (состояние отказа). Вероятности переходов между состояниями характеризуются интенсивностями отказов λikи интенсивностями восстановления μki. Исходя из заданных значений интенсивностей отказов λikи интенсивностей восстановления μki, найти параметры надежности (предполагая простейший поток отказов): 1) финальные вероятности нахождения системы во всех состояниях, в том числе вероятность отказа системы Qс; 2) среднее время наработки на отказ Тсри интенсивность отказов системы λс; 3) среднее время восстановления Тв; 4) коэффициент готовности Кг; 5) среднее время безотказной работы (среднюю наработку до отказа) Тот.  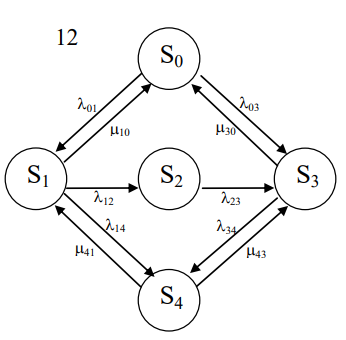 Рис. 1. Граф состояний системы Выбор численных параметров λik =λ= n∙10-4 =16∙10-4 (1/ч) μik=μ= 10/n= 0,625 (1/ч) Расчет показателей надежности дублированной восстанавливаемой системы Исходя из графа, система может находиться в одном из 5 состояний: 0 исправное состояние; 1–1-е работоспособное состояние: отказал первый элемент (находится в ремонте), второй, третий – исправен; 2–2-е работоспособное состояние: отказал второй элемент (находится в ремонте), первый, третий – исправен; 3–3-е работоспособное состояние: отказал третий элемент (находится в ремонте), первый, второй – исправен; 4–неработоспособное состояние (состояние отказа): отказали последовательно три элемента и находятся в состоянии ремонта. Составим систему уравнений Колмогорова для финальных вероятностей нахождения во всех состояниях:  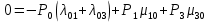 ; ;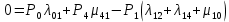 ; ;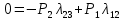 ; ;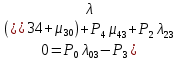 ; ;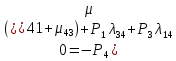 ; ;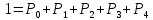 . .Подставим численные значения: 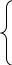 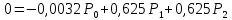 ; ;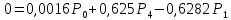 ; ;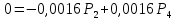 ; ;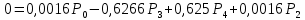 ; ;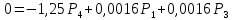 ; ;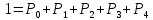 . .Решение системы для финальных вероятностей нахождения во всех состояниях методом Крамера:   -0,0032 -0,0032 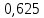 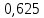 0 0 0 0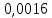 - -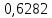 0 0 0 0 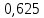 Δ = 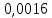 0 0 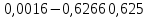 = -0.03091 = -0.03091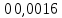 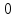 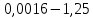 1 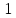 1 1 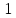 1 1   0 0 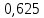 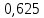 0 0 0 0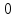 - -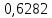 0 0 0 0 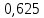 0Δ = 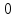 0 0 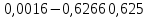 = -0.03091 = -0.03091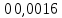 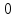 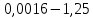 1 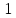 1 1 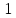 1 1  -0,0034 0 0,588 0 0 -0,0034 0 0,588 0 00,0017 0 0 0 0 Δ1= 0 0 -0,588 0 0,588 = -9,9920016∙10-7 0 0 -0,588 0,0017 -0,588 1 1 1 1 1   -0,0034 0,588 0 0 0 -0,0034 0,588 0 0 00,0017 -0,588 0 0 0 Δ2= 0 0 0 0 0,588 = -9,9920016∙10-7 0 0 0 0,0017 -0,588 1 1 1 1 1   -0,0034 0,588 0,588 0 0 -0,0034 0,588 0,588 0 00,0017 -0,588 0 0 0 Δ3= 0 0 -0,588 0 0,588 = -0,0006912 0 0 -0,588 0 -0,588 1 1 1 1 1   -0,0034 0,588 0,588 0 0 0,0017 -0,588 0 0 0 Δ4= 0 0 -0,588 0 0 = -9,9920016∙10-7 0 0 -0,588 0,0017 0 1 1 1 1 1 x0 = 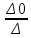 = = 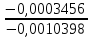 = 0,3324 = 0,3324x1 = 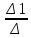 = = 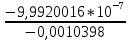 = 0,001 = 0,001x2 = 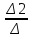 = = 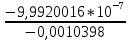 = 0,001 = 0,001x3 = 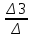 = = 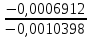 = 0,6647 = 0,6647x4 = 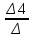 = = 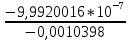 = 0,001 = 0,001Получаем: 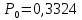 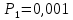 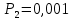 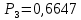 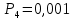 Найдем вероятность отказа системы и вероятность безотказной работы: 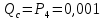 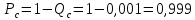 Зная финальные вероятности, найдем время наработки на отказ 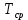 , интенсивность отказов системы , интенсивность отказов системы 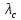 , среднее время восстановления , среднее время восстановления 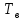 , коэффициент готовности , коэффициент готовности 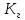 . .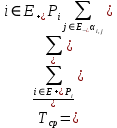 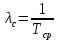 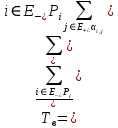 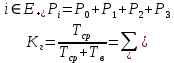 где 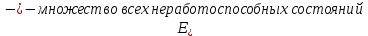 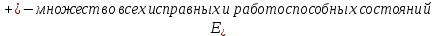 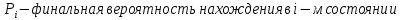 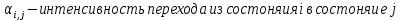 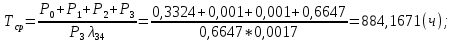 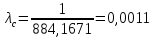 (1/ч); (1/ч);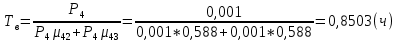 ; ;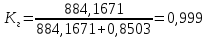 ; ;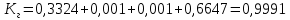 . .Для нахождения среднего времени безотказной работы (среднего времени наработки до отказа) выполним преобразование Лапласа для уравнения Колмогорова с учетом начальных условий. В результате получим систему уравнений: 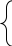 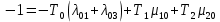 ; ;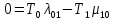 ; ;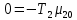 ; ;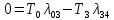 . .Подставим численные значения: 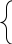 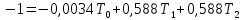 ; ;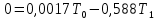 ; ;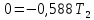 ; ;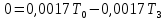 . .Решение системы для нахождения среднего времени безотказной работы методом Крамера:   -0,0034 0,588 0,588 0 0,0017 -0,588 0 0 Δ = 0 0 -0,588 0 = 9,9920016∙10-7 0,0017 0 0 -0,0017   -1 0,588 0,588 0 0 -0,588 0 0 Δ0 = 0 0 -0,588 0 = 0,0005878 0 0 0 -0,0017   -0,0034 -1 0,588 0 0,0017 0 0 0 Δ1 = 0 0 -0,588 0 = 1,69932∙10-6 0,0017 0 0 -0,0017   -0,0034 0,588 -1 0 0,0017 -0,588 0 0 Δ2 = 0 0 0 0 = 0 0,0017 0 0 -0,0017   -0,0034 0,588 0,588 -1 0,0017 -0,588 0 0 Δ3 = 0 0 -0,588 0 = 0,0005878 0,0017 0 0 0 x0 = 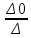 = = 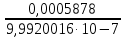 = 588,2705 = 588,2705x1 = 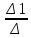 = = 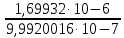 = 1,7007 = 1,7007x2 = 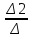 = = 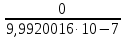 = 0 = 0x3 = 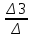 = = 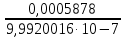 = 588,2705 = 588,2705Получаем: 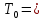 588,2353 (ч) 588,2353 (ч)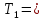 1,7007 (ч) 1,7007 (ч)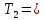 0 (ч) 0 (ч)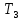 =588,2353 (ч) =588,2353 (ч)Среднее время безотказной работы (средняя наработка до отказа): 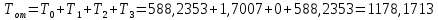 (ч) (ч) |
