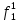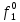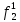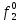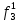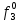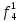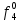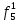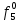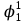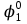Курсовой проект по дисциплине Основы теории надежности тема работы Методы расчета показателей надежности сжат
 Скачать 428.29 Kb. Скачать 428.29 Kb.
|
2. Расчет надежности комбинационных схемВариант 26 Значение вероятностей появления входных переменных: p1=0,2; р2=0,4; р3=0,9 С помощью логической функции, заданной в алгебраическом виде построим комбинационную схему на двухвходовых логических элементах. 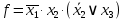 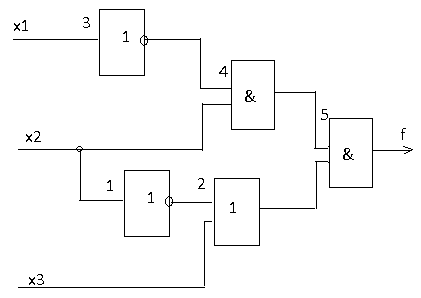 Рис. 1 Для анализа комбинационной схемы построим таблицу истинности. Таблицу истинности построим по логической формуле ФАЛ. Для этого в логическую формулу функции нужно подставить все возможные значения входных переменных и вычислить значения функции. Таблица 1
При расчетах надежности принимается допущение об одиночных константных неисправностях. Неисправность логического элемента приводит на выходе элемента к отказам двух видов: - ложное появление сигнала 1 вместо 0. 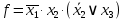 - ложное появление сигнала 0 вместо 1. 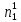 : : 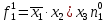 : : 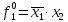 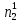 : : 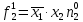 : : 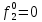 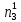 : : 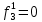 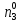 : : 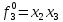 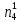 : : 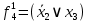 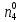 : : 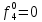 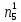 : : 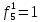 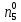 : : 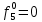 По полученным формулам построим таблицу неисправностей, где 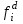 - функция, реализуемая схемой при неисправности i-го логического элемента типа d. - функция, реализуемая схемой при неисправности i-го логического элемента типа d.Таблица 2
Введем понятие функции ошибки 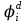 . Эта функция выделяет те наборы , для которых неисправность является существенной. . Эта функция выделяет те наборы , для которых неисправность является существенной.Так как по определению 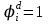 , если , если 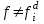 , то тогда определение соответствует формуле: , то тогда определение соответствует формуле: 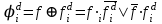 . . Таким образом, в соответствии с определением функция ошибки равна 1 для наборов, на которых неисправность является существенной. Таблица 3
Произведя подобные вычисления для сбоев типа 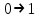 и и 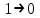 всех шести элементов схемы, получим: всех шести элементов схемы, получим: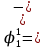 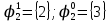 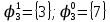 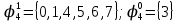 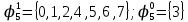 При расчете надежности следует учитывать, что вероятность отказа элемента зависит не только от характера неисправности - ni , но и от вероятности появления входных наборов. Определим вероятности Rk появления входных наборов. Появление всех входных наборов составляет полную группу событий, поэтому 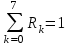 где k – номера входных наборов. Составим таблицу, отражающую полную группу событий на входе схемы. Результаты расчета приведены в таблице 4. Таблица 4
Определим вероятность истинности функции f как сумму вероятностей разрешенных наборов, т.е. таких, на которых функция f равна 1: 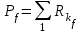 . .В рассматриваемом случае: Pf= R3 =0,288 Определим вероятности истинности функций ошибки как условные вероятности того, что на выходе схемы происходит ошибка при наличии сбоя 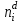 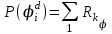 где 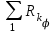 - сумма вероятностей тех наборов, на которых функция - сумма вероятностей тех наборов, на которых функция 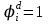 . .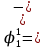 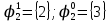 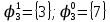 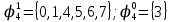 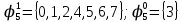 В нашем случае: P( 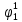 )= - P( )= - P(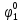 )= R2 =0,032 )= R2 =0,032 P( 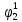 )= R2 =0,032 P( )= R2 =0,032 P(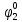 )= R3 =0,288 )= R3 =0,288P( 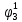 )= R3 =0,288 P( )= R3 =0,288 P(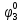 )= R7 =0,072 )= R7 =0,072P( 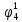 )= R0+R1+R4+R5+R6+R7= 1,112 P( )= R0+R1+R4+R5+R6+R7= 1,112 P(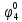 )= R3 =0,288 )= R3 =0,288P( 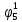 )= R0+R1+ R2+R4+R5+R6+R7= 1,144 P( )= R0+R1+ R2+R4+R5+R6+R7= 1,144 P(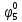 )= R3 =0,288 )= R3 =0,288Далее необходимо определить вероятность появления неисправности в момент времени. Допустим, что вероятности сбоев 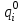 и и 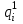 для всех элементов одинаковые и равны для всех элементов одинаковые и равны 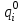 = = 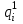 = 0,001. = 0,001. В этом случае: 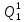 =- =- 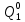 =0,001*0,032=0,32*10-4 =0,001*0,032=0,32*10-4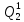 =0,001*0,032=0,32*10-4 =0,001*0,032=0,32*10-4 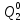 =0,001*0,288=2,88*10-4 =0,001*0,288=2,88*10-4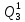 =0,001*0,288=2,88*10-4 =0,001*0,288=2,88*10-4 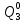 =0,001*0,072=0,72*10-4 =0,001*0,072=0,72*10-4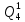 =0,001*1,112=11,12*10-4 =0,001*1,112=11,12*10-4 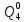 =0,001*0,288=2,88*10-4 =0,001*0,288=2,88*10-4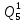 =0,001*1,144=11,44*10-4 =0,001*1,144=11,44*10-4 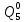 =0,001*0,288=2,88*10-4 =0,001*0,288=2,88*10-4Вероятность ошибки на выходе схемы в момент времени t определяется по следующей формуле: 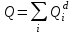 Для нашего примера: Q=10-4*(0,32+0,32+2,88+2,88+2,88+2,88+0,72+11,12+11,44)=35,44*10-4. Соответственно, вероятность отсутствия ошибки на выходе схемы, т.е. вероятность исправной работы схемы равна: P = 1 – Q P = 1 –35,44*10-4=0,996456 |