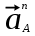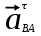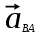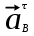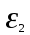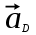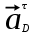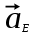Курсовая работа по прикладной механике и деталям машин. приклад курсач. Курсовой проект по прикладной механике является самостоятельной работой студента, завершающей изучение этой дисциплины. В процессе разработки проекта применены
 Скачать 1.73 Mb. Скачать 1.73 Mb.
|
3.3 Определение ускорений точек механизма и угловых ускорений звеньев механизма. План ускорений механизмаДля определения ускорений точек механизма воспользуемся графоаналитическим методом расчета с помощью построения плана ускорений механизма. План ускорений механизма (ПУМ) – графическое векторное масштабное изображение ускорений точек механизма для заданного положения механизма. Для построения ПУМ необходимо аналитически определить линейное ускорение точки А кривошипа, которое определяется по следующему векторному уравнению: 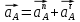 , м/с2 (3.7) , м/с2 (3.7)где 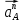 - нормальная составляющая ускорения точки А, м/с-2; - нормальная составляющая ускорения точки А, м/с-2;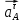 - тангенциальная составляющая ускорения точки А, м/с-2. - тангенциальная составляющая ускорения точки А, м/с-2.Так как кривошип ОА имеет постоянную угловую скорость  , то точка А вращается равномерно и , то точка А вращается равномерно и 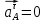 , поэтому уравнение (3.7) можно преобразовать к следующему виду: , поэтому уравнение (3.7) можно преобразовать к следующему виду: , м/с2 . (3.8) , м/с2 . (3.8)Нормальная составляющая ускорения точки, А 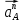 направлена параллельно ОА от точки А к точке О и определяется по следующей зависимости: направлена параллельно ОА от точки А к точке О и определяется по следующей зависимости: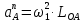 . (3.9) . (3.9)Для определения ускорения точки В запишем векторное уравнение: 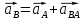 . (3.10) . (3.10)Звено 3 совершает неравномерное вращательное движение относительно неподвижной точки С, поэтому вектор абсолютного ускорения точки В определится из следующего векторного уравнения:  , м/с2 . (3.11) , м/с2 . (3.11)Звено 2 совершает плоскопараллельное сложное движение, поэтому вектор относительного ускорения точки В относительно подвижной точки А определится из следующего векторного уравнения: 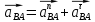 , м/с2. (3.12) , м/с2. (3.12)Таким образом, векторное уравнение (3.12) с учетом (3.8), (3.10) и (3.11) преобразуется к следующему виду:  . (3.13) . (3.13)Найдем величины нормальных составляющих входящих в векторное уравнение 3.13. Нормальная составляющая ускорения точки А 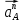 направлена || ОА от точки А к точке О и определяется по следующей зависимости: направлена || ОА от точки А к точке О и определяется по следующей зависимости: м/с2. м/с2.Нормальная составляющая абсолютного ускорения точки В  направлена || ВС от точки В к точке С и определяется по следующей зависимости: направлена || ВС от точки В к точке С и определяется по следующей зависимости: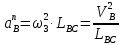 , м/с2. (3.14) , м/с2. (3.14)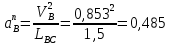 м/с2. м/с2.Нормальная составляющая относительного ускорения точки В относительно точки А 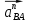 направлена || АВ от точки В к точке А и определяется по следующей зависимости: направлена || АВ от точки В к точке А и определяется по следующей зависимости: , м/с2. (3.15) , м/с2. (3.15)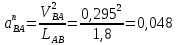 м/с2. м/с2.Анализируем векторное уравнение (3.13). Касательная составляющая абсолютного ускорения точки В ( 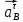 ) известна по направлению, так как точка В в своем абсолютном движении совершает вращательное движение вокруг точки С, то ее касательное ускорение будет перпендикулярно участку ВС звена 3 ( ) известна по направлению, так как точка В в своем абсолютном движении совершает вращательное движение вокруг точки С, то ее касательное ускорение будет перпендикулярно участку ВС звена 3 ( ). ). Касательная составляющая относительного ускорения точки В относительно точки А ( 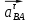 ) известна по направлению, так как точка В в своем относительном движении совершает вращательное движение вокруг точки А, то ее касательное ускорение будет перпендикулярно звену АВ ( ) известна по направлению, так как точка В в своем относительном движении совершает вращательное движение вокруг точки А, то ее касательное ускорение будет перпендикулярно звену АВ (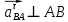 ). ).Ускорения известные только по направлению подчеркиваем одной чертой, а известные по направлению и величине – двумя. Анализ векторного уравнения (3.13) показал, что неизвестны только два ускорения по величине, и такое уравнение решается графически. Неизвестные ускорения точек механизма находим графически, путем построения плана ускорений. Для этого определим масштаб ПУМ: 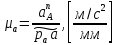 , (3.16) , (3.16)где 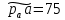 - отрезок на плане ускорений механизма в миллиметрах, изображающий ускорение - отрезок на плане ускорений механизма в миллиметрах, изображающий ускорение  . . Переводим все известные ускорения в отрезки через масштаб плана ускорений механизма и результаты сводим в таблицу 3. Т а б л и ц а 3 – Размеры отрезков на ПУМ
Так как ускорении  невелико, то на ПСМ данная точка совпадает с точкой а невелико, то на ПСМ данная точка совпадает с точкой аВыбираем на плоскости произвольную точку 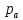 - полюс плана ускорений и из нее в направлении ускорения - полюс плана ускорений и из нее в направлении ускорения 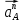 откладываем вектор равный откладываем вектор равный 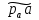 . Из конца полученного вектора откладываем вектор . Из конца полученного вектора откладываем вектор  от точки В к точке А. Через конец полученного векторапроводим линию действия от точки В к точке А. Через конец полученного векторапроводим линию действия 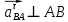 . Из полюса построения . Из полюса построения 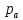 откладываем вектор откладываем вектор 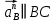 от точки В к точке С, через конец которого проводим линию действия от точки В к точке С, через конец которого проводим линию действия  . Точка пересечения линий действия . Точка пересечения линий действия 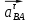 и и 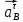 дает решение векторного уравнения 3.13 (см. план ускорений механизма на формате). Из полюса дает решение векторного уравнения 3.13 (см. план ускорений механизма на формате). Из полюса 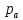 в точку в точку  проводим вектор полного абсолютного ускорения точки В ( проводим вектор полного абсолютного ускорения точки В (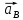 ), а из точки ), а из точки 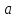 в точку в точку  плана ускорений механизма проводим вектор полного относительного ускорения точки В относительно точки А ( плана ускорений механизма проводим вектор полного относительного ускорения точки В относительно точки А (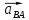 ). Измерив соответствующие отрезки на плане ускорений и умножив их на масштаб ). Измерив соответствующие отрезки на плане ускорений и умножив их на масштаб 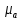 , определим ускорения , определим ускорения 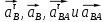 Результаты построений и вычислений сводим в таблицу 4. Результаты построений и вычислений сводим в таблицу 4.Т а б л и ц а 4 – Сводная таблица ускорений точек А и В и звеньев 2, 3 механизма
Определяем угловые ускорения звеньев 2 и 3 по зависимости:  , с-2. (3.17) , с-2. (3.17)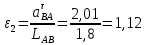 , с-2. , с-2. с-2. с-2.Учитывая, что все точки звена 3 имеют одинаковое угловое ускорение 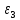 , определяем линейные ускорения точек , определяем линейные ускорения точек 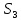 и D методом подобия из соотношений: и D методом подобия из соотношений: , откуда , откуда 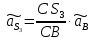 . (3.18) . (3.18)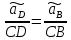 , откуда , откуда  . (3.19) . (3.19) 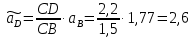 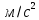 . .Переводим известные ускорения точек D и S3 в отрезки через масштаб ПУМ: 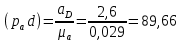 мм. мм.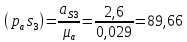 мм. мм.Для определения ускорения точки Е запишем векторное уравнение: 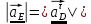 (3.20) (3.20) Анализируем векторное уравнение (3.20). Ускорение точки E ( 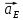 ) известно по направлению, так как точка E в своем абсолютном движении совершает прямолинейное возвратно–поступательное движение вдоль направляющей, то ее ускорение будет параллельно направляющей ) известно по направлению, так как точка E в своем абсолютном движении совершает прямолинейное возвратно–поступательное движение вдоль направляющей, то ее ускорение будет параллельно направляющей  ( (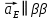 ). ).Звено 4 совершает плоскопараллельное сложное движение, поэтому вектор относительного ускорения точки D относительно подвижной точки C определится из следующего векторного уравнения:  , м/с2. (3.21) , м/с2. (3.21)Нормальная составляющая относительного ускорения точки D относительно точки C  направлена || CD от точки D к точке C и определяется по следующей зависимости: направлена || CD от точки D к точке C и определяется по следующей зависимости: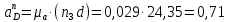 м/с2. м/с2. м/с2. м/с2.Касательная составляющая относительного ускорения точки E относительно точки D ( 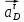 ) известна по направлению, так как точка E в своем относительном движении совершает вращательное движение вокруг точки D, то ее касательное ускорение будет перпендикулярно звену СD ( ) известна по направлению, так как точка E в своем относительном движении совершает вращательное движение вокруг точки D, то ее касательное ускорение будет перпендикулярно звену СD ( ). ).Ускорение точки D ( 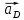 ) известно по направлению, так как точка D в своем абсолютном движении совершает вращательное движение вокруг неподвижной точки С, являющейся мгновенным центром ускорений звена 3, поэтому ) известно по направлению, так как точка D в своем абсолютном движении совершает вращательное движение вокруг неподвижной точки С, являющейся мгновенным центром ускорений звена 3, поэтому 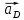 направлено параллельно ускорению направлено параллельно ускорению 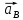 . .Ускорения известные только по направлению подчеркиваем одной чертой, а известные по направлению и величине – двумя. Анализ векторного уравнения показал, что неизвестны только два ускорения по величине, и такое уравнение решается графически. Неизвестные ускорения точек механизма находим графически, путем построения плана ускорений. Из конца полученного вектора 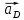 откладываем в выбранном масштабе вектор откладываем в выбранном масштабе вектор 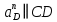 от точки D к точке C. Через конец полученного векторапроводим линию действия от точки D к точке C. Через конец полученного векторапроводим линию действия 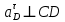 . Из полюса построения . Из полюса построения 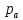 проводим линию действия проводим линию действия 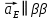 . Точка пересечения линий действия . Точка пересечения линий действия 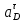 и и 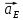 дает решение векторного уравнения (см. план ускорений механизма на формате). Из полюса дает решение векторного уравнения (см. план ускорений механизма на формате). Из полюса 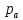 в точку в точку  проводим вектор полного абсолютного ускорения точки E ( проводим вектор полного абсолютного ускорения точки E (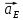 ), а из точки ), а из точки 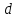 в точку в точку  плана ускорений механизма проводим вектор полного относительного ускорения точки E относительно точки D ( плана ускорений механизма проводим вектор полного относительного ускорения точки E относительно точки D (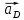 ). ). Измерив соответствующие отрезки на плане ускорений механизма и умножив их на масштаб 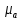 , определим ускорения , определим ускорения 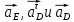 . Результаты построений и вычислений сводим в таблицу 5. . Результаты построений и вычислений сводим в таблицу 5.Т а б л и ц а 5 – Сводная таблица ускорений точек D и E и звена 4 механизма
Угловые ускорения звеньев механизма направлены в сторону тангенциальных составляющих линейных ускорений. 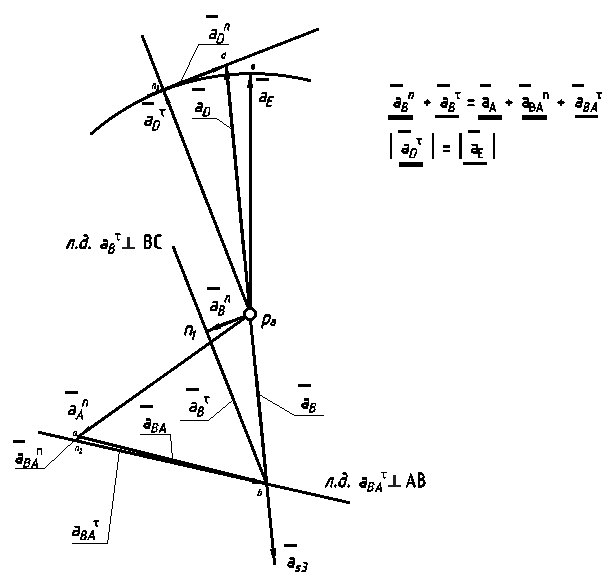 Рисунок 5 - План ускорений механизма |

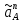 , мм
, мм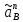 , мм
, мм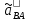 , мм
, мм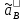 , мм
, мм , мм
, мм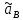 , мм
, мм